Уравненные значения углов.

№ углов	Измеренные значения	Поправки Vi	Уравненные значения
1
2
3
4
5
6

Оценка точности:

1. СКО измерений:

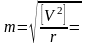
2. Ошибка ошибки:

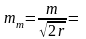
3. СКО функции F:

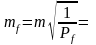
4. Ошибка самой ошибки:

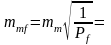
Контрольная работа № 2 «Уравновешивание неравноточных измерений».

1. Задание.

Выполнить уравнивание параметрическим способом результатов нивелирования. Определить наиболее надежные значения отметок узловых реперов на среднюю квадратическую ошибку нивелирования на один условный километр хода, считая в 1 км 10 станций. Оценку точности уравненных высот I, II, III и разности уравненных отметок H_III – H_I провести при помощи весовых коэффициентов.

2. Схема нивелирной сети.

3. Исходные данные.

№ ходов	Превышение h, м	Число станций
1	+1,953	40 «+»
2	-0,934	42
3	+1,014	30
4	-0,406	37
5	+0,621	45 «-»
6	-0,912	60
7	-0,417	50
8	+0,513	52

Результаты нивелирования по ходам.

Высота опорных марок:

Марки	Высота Н, м
А	320,355
В	321,897

4. Выбор параметров.

В качестве необходимых неизвестных выбираем отметки узловых реперов I, II, III

Т₁=Н₁; Т₁=Н₁; Т₁=Н₁.

5. Приближенные значения параметров.

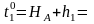
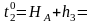
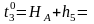
6. Уравнение связи.

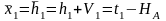
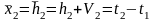
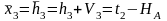
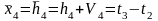
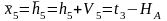
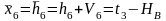
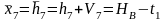
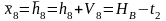
7. Определяем коэффициенты и свободные члены уравнений поправок.

; ; ;

; ; ;

; ; ;

; ; ;

; ; ;

; ; ;

; ; ;

; ; .

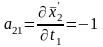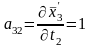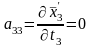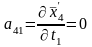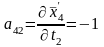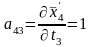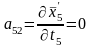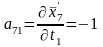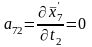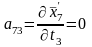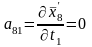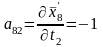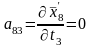Формулы свободных членов:

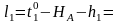
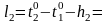
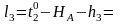
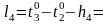
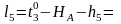
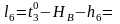
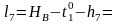
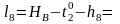
8. Составляем уравнения поправок:

V₁ = a₁₁τ₁ + a₁₂τ₂ + a₁₃τ₃ + l₁

V₂ = a₂₁τ₁ + a₂₂τ₂ + a₂₃τ₃ + l₂

V₃ = a₃₁τ₁ + a₃₂τ₂ + a₃₃τ₃ + l₃

V₄ = a₄₁τ₁ + a₄₂τ₂ + a₄₃τ₃ + l₄

V₅ = a₅₁τ₁ + a₅₂τ₂ + a₅₃τ₃ + l₅

V₆ = a₆₁τ₁ + a₆₂τ₂ + a₆₃τ₃ + l₆

V₇ = a₇₁τ₁ + a₇₂τ₂ + a₇₃τ₃ + l₇

V₈ = a₈₁τ₁ + a₈₂τ₂ + a₈₃τ₃ + l₈

Таблица коэффициент уравнений поправок и нормальных уравнений.

№ п/п		ai1	ai1	ai1	li	Si	Vi, см	PiViVi	PiliVi
1
2
3
4
5
6
7
8
Σ
		Ni1	Ni2	Ni3	Li	Σi	контроль
N1jL1								[Pll] =
N2jL2								[PlS] =
N3jL3								[PSS] =

N₁₁ = [Pa₁a₁] = P₁a₁₁a₁₁ + P₂a₁₂a₁₂ + P₃a₁₃a₁₃ + P₄a₁₄a₁₄ + P₅a₁₅a₁₅ + P₆a₁₆a₁₆ + P₇a₁₇a₁₇ + P₈a₁₈a₁₈ =

N₁₂ = [Pa₁a₂] = P₁a₁₁a₁₂ + P₂a₂₂a₂₂ + P₃a₃₁a₃₂ + P₄a₄₁a₄₂ + P₅a₅₁a₅₂ + P₆a₆₁a₆₂+ P₇a₇₁a₇₂ + P₈a₈₁a₈₂ =

N₁₃ = [Pa₁a₃] = P₁a₁₁a₁₃ + P₂a₂₂a₂₃ + P₃a₃₁a₃₃ + P₄a₄₁a₄₃ + P₅a₅₁a₅₃ + P₆a₆₁a₆₃+ P₇a₇₁a₇₃ + P₈a₈₁a₈₃ =

N₂₂ = [Pa₂a₂] = P₁a₁₂a₁₂ + P₂a₂₂a₂₂ + P₃a₃₂a₃₂ + P₄a₄₂a₄₂ + P₅a₅₂a₅₂ + P₆a₆₂a₆₂ + P₇a₇₂a₇₂ + P₈a₈₂a₈₂ =

N₂₃₂ = [Pa₂a₃] = P₁a₁₂a₁₃ + P₂a₂₂a₂₃ + P₃a₃₂a₃₃ + P₄a₄₂a₄₃ + P₅a₅₂a₅₃ + P₆a₆₂a₆₃ + P₇a₇₂a₇₃ + P₈a₈₂a₈₃=

N₃₃ = [Pa₃a₃] = P₁a₁₃a₁₃ + P₂a₂₃a₂₃ + P₃a₃₃a₃₃ + P₄a₄₃a₄₃ + P₅a₅₃a₅₃+ P₆a₆₃a₆₃ + P₇a₇₃a₇₃+ P₈a₈₃a₈₃ =

L₁ = = [Pa₁l₁] = P₁a₁₁l₁ + P₂a₂₁l₂ + P₃a₃₁l₃ + P₄a₄₁l₄ + P₅a₅₁l₅ + P₆a₆₁l₆ + P₇a₇₁l₇ + P₈a₈₁l₈ =

L₂ = = [Pa₂l₂] = P₁a₁₂l₁ + P₂a₂₂l₂ + P₃a₃₂l₃ + P₄a₄₂l₄ + P₅a₅₂l₅ + P₆a₆₂l₆ + P₇a₇₂l₇ + P₈a₈₂l₈ =

L₃ = = [Pa₃l₃] = P₁a₁₃l₁ + P₂a₂₃l₂ + P₃a₃₃l₃ + P₄a₄₃l₄ + P₅a₅₃l₅ + P₆a₆₃l₆ + P₇a₇₃l₇ + P₈a₈₃l₈ =

9.После заполнения таблицы выполняем контроль подсчетов, для которого определяют 3 суммы:

Σ₁= N₁₁ + N₁₂ + N₁₃ + L₁=

Σ₂= N₂₁ + N₂₂ + N₂₃ + L₂=

Σ₃= N₃₁ + N₃₂ + N₃₃ + L₃=

[PlS] = L₁ + L₂ + L₃ + [Pll] =

[PSS] = Σ₁ + Σ₂ + Σ₃ + [PlS] =