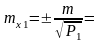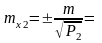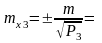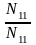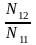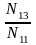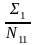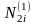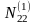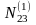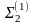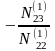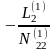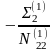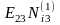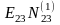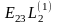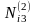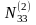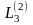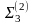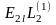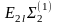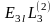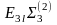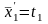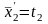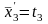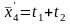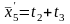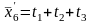Контрольная работа № 1
выполняется в пределах СМ-2
студентами очного обучения и
в качестве семестровой контрольной работы
студентами 2 курса заочного обучения (3 семестр)
по вариантам, выдаваемым преподавателем
Контрольная работа № 2
выполняется в пределах СМ-2
студентами очного обучения и
в качестве семестровой контрольной работы
студентами 2 курса заочного обучения (4 семестр)
по вариантам, выдаваемым преподавателем
Контрольная работа № 1 «Уравнивание равноточных измерений»
1.Задание.
На пункте О измерены углы между направлениями ОА, ОВ, ОС во всех возможных комбинациях. Выполнить оценку углов и дать оценку точности параметрическим способом.
2.Схема.
х4 = х1 + х2
х5 = х2 + х3
х6 = х1 + х2+ х3
3.Исходные данные.
|
Градусы (°) |
Минуты (') |
Секунды (") |
Добавка в секунды(") |
Х 1 |
45 |
22 |
02 |
+ |
Х 2 |
41 |
29 |
20 |
|
Х 3 |
32 |
38 |
20 |
|
Х 4 |
86 |
51 |
20 |
|
Х 5 |
74 |
07 |
44 |
- |
Х 6 |
119 |
29 |
52 |
|
4.Условные обозначения параметрических и нормальных уравнений:
Хi – истинное значение измерений;
хi – результаты измерений;
Тi – истинное значение необходимых неизвестных параметров;
t i0– приближенное значение параметров;
τi – поправки к ближайшим значениям параметров;
аjk – коэффициенты поправок параметрических уравнений;
li – свободные члены параметрических уравнений;
Njk – коэффициенты нормальных уравнений;
Li – свободные члены нормальных уравнений;
Vi –поправки параметрических уравнений;
xi' – уравненные значения измеренных величин.
В процессе уравнивания принимаем ближайшие значения параметров, находим поправки к ним и вычисляем уравненные значения параметров t i.
Зная параметры поправок находим уравненные значения измеренных величин.
5.Выбор параметров.
Выбираем: Т1=Х1; Т2=Х2; Т3=Х3.
6.Приближенные значения параметров.
ti0 = х1 =
t20= х2 =
t30= х3 =
7.Уравнения связи.
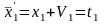
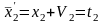
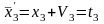(1)
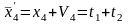
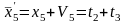
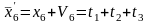
Для определения поправок Vi составляем систему параметрических уравнений в виде:
V1=а11τ1+а12τ2+а13τ3+l1
V2=а21τ1+а22τ2+а23τ3+l2
V3=а31τ1+а32τ2+а33τ3+l3
V4=а41τ1+а42τ2+а43τ3+l4 (2)
V5=а51τ1+а52τ2+а53τ3+l5
V6=а61τ1+а62τ2+а63τ3+l6
Вычисляем коэффициенты аjk и свободные члены системы (2). Находим частные производные уравнений системы (1).
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
;
.
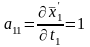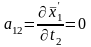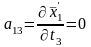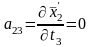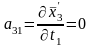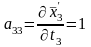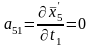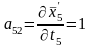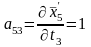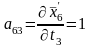Формулы свободных членов уравнений поправок:
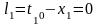
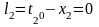
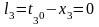
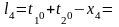
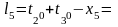
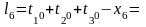
Таблица коэффициентов поправок и нормальных уравнений.
№ п/п |
aj1 |
aj1 |
aj1 |
l1 |
S1 |
V1 |
1 |
1 |
0 |
0 |
0 |
1 |
|
2 |
0 |
1 |
0 |
0 |
1 |
|
3 |
0 |
0 |
1 |
0 |
1 |
|
4 |
1 |
1 |
0 |
|
|
|
5 |
0 |
1 |
1 |
|
|
|
6 |
1 |
1 |
1 |
|
|
|
Σ |
|
|
|
|
|
|
|
Nj1 |
Nj2 |
Nj3 |
Lj |
Σj |
контроль |
1 |
3 |
2 |
1 |
|
|
|
2 |
2 |
4 |
2 |
|
|
|
3 |
1 |
2 |
3 |
|
|
|
[u], [lS] |
|
|
|
|
|
|
[SS] |
|
|
|
|
|
|
V1 = τ1 =
V2 = τ2 =
V3 = τ3 =
V4 = τ1 + τ2 + l4=
V5 = τ2 + τ3 + l5=
V6 = τ1 + τ2 + τ3+ l6=
Для определения τ1, τ2, τ3 составляем систему нормальных уравнений:
N11τ1 + N12τ2 + N13τ3 + L1 = 0
N21τ1 + N22τ2 + N23τ3 + L2 = 0 (3)
N31τ1 + N32τ2 + N33τ3 + L3 = 0
N11 = [a1a1] = a11 a11 + a12 a12 + a13 a13 + a14 a14 + a15 a15 + a16 a16 = 3
N12 = [a1a2] = a11 a12 + a21 a22 + a31 a32 + a41 a42 + a51 a52 + a61 a62 = 2
N13 = [a1a3] = a11 a13 + a21 a23 + a31 a33 + a41 a43 + a51 a53 + a61 a63 = 1
N22 = [a2a2] = a12 a12 + a22 a22 + a23 a23 + a24 a24 + a25 a25 + a26 a26 = 4
N23 = [a2a3] = a12 a12 + a22 a23 + a33 a33 + a42 a43 + a52 a53 + a62 a63 = 2
N33 = [a3a3] = a13 a13 + a23 a23 + a33 a33 + a43 a43 + a53 a53 + a63 a63= 3
L1 = [a1 l1] = a11 l1 + a21 l2 + a31 l4 + a41 l4 + a51 l5 + a61 l6 =
L2 = [a2 l2] = a12 l1 + a22 l2 + a32 l4 + a42 l4 + a52 l5 + a62 l6 =
L3 = [a3 l3] = a13 l1 + a23 l2 + a33 l4 + a43 l4 + a53 l5 + a63 l6 =
После заполнения таблицы выполняем контроль подсчетов, для которого определяют 3 суммы:
Σ1 = N11 + N12 + N13 + L1 =
Σ2 = N21 + N22 + N23 + L2 =
Σ3 = N31 + N32 + N33 + L3 =
Уравнение контроля:
[SS] = Σ1 + Σ2 + Σ3 + [l S] =
[l S] = L1 + L2 + L3 + [l l] =
|
τ1 |
τ2 |
τ3 |
L |
Σ |
контроль |
||||||||||||||
0 |
1 |
2 |
3 |
4 |
5 |
6 |
||||||||||||||
Nil |
N11 |
|
N12 |
|
N13 |
|
L1 |
|
Σ1 |
|
|
|||||||||
Eli |
- |
|
- |
|
- |
|
- |
|
- |
|
|
|||||||||
N2i |
|
N22 |
|
N23 |
|
L2 |
|
Σ2 |
|
|
||||||||||
Ni2 Ei2 |
N12E12 |
|
N13 E12 |
|
L1 E12 |
|
Σ1 E12 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
E2i
|
|
|
|
|
|
|
|
|
|
|||||||||||
N3i |
|
N33 |
|
L3 |
|
Σ3 |
|
|
||||||||||||
E13 Ni3 |
E13N13 |
|
E13L1 |
|
E13Σ1 |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||
E3i |
|
|
|
|
|
|
|
|||||||||||||
ll, SS |
|
[ll] |
|
[lS] |
|
|
||||||||||||||
|
|
E1lL1 |
|
E1lΣ1 |
|
|
||||||||||||||
|
E1lL1 |
|
E1lΣ1 |
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|||||||||||||||
|
[V2] = |
|
[ll](3) |
|
[lS](3) |
|
|
|||||||||||||
τ3 |
|
|
|
E3l |
|
|
|
τ3 = E3l |
|
|
||||||||||
τ2 |
|
τ2 |
|
E23τ3 |
|
E2l |
|
τ2 = E23τ3+ E2l |
|
|
||||||||||
τ1 |
τ1 |
|
E12τ2 |
|
E13τ3 |
|
E1l |
|
τ1 = E12τ2 + E13τ3 + E1l |
|
|
|||||||||
Контроль:
E11 + E12 + E13 + E1l = E1
E22 + E23 + E2l = E2
E33 + E3l = E3
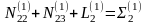
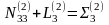
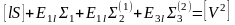
№ угла |
Измеренные значения |
Vi" |
Уравненный угол |
Уравнение связи |
Контроль |
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
|
Оценка точности вычислений СКО измеренного угла
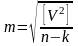
Веса углов х1; х2; х3
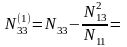
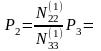
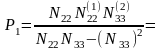
СКО измерения углов:
