П.4. Геометрическая интерпретация и графическое решение злп

Можно решить графически ЗЛП сформулированную:

- в симметричной форме или в общем виде с двумя переменными;

- в канонической форме с двумя свободными переменными.

Рассмотрим ЗЛП:

(7)

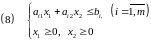
Каждое ограничение (8) задает на плоскости 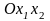полуплоскость, которая представляет собой выпуклое множество. Пересечение (общая часть) выпуклых множеств – также выпуклое. Следовательно, область допустимых планов ЗЛП выпуклое множество. Оно может иметь следующий вид:

a. выпуклый замкнутый многоугольник (имеется максимум и минимум целевой функции; если линия уровня параллельна границе многоугольника – решений множество, имеется альтернативный оптимум; если несколько ограничений пересекаются в одной угловой точке – решение вырожденное)

Пример 3:

b. выпуклый незамкнутый многоугольник (не существует либо максимум, либо минимум неограниченной целевой функции)

Пример 4:

c. отрезок, точка

Пример 5:
Пример 6:

- пустое множество (решений ЗЛП нет – условия неравенства – противоречивы)

Пример 7:

Пусть область допустимых планов ЗЛП – непустое множество (многоугольник). Выбрав произвольное значение целевой функции получают равенство 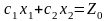(графически – это уравнение прямой). В точках построенной прямой целевая функция сохраняет одно и то же значение . При различных значениях 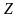получают семейство параллельных прямых, называемых линиями уровня целевой функции.

Чтобы установить направление возрастания целевой функции найдем частные производные целевой функции по 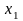и : ; . Вектор является градиентом целевой функции.

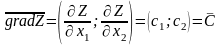
Он задает направление наискорейшего возрастания функции, а направление наискорейшего убывания функции задает вектор

,

называемый антиградиентом. Вектор перпендикулярен прямым .

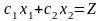Алгоритм графического решения злп.

1. на основе системы ограничений строится область допустимых планов ЗЛП.

2. строится вектор наискорейшего возрастания целевой функции –градиент (если в ЗЛП требуется минимизировать целевую функцию строят антиградиент).

3. проводится произвольная линия уровня 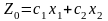(обычно это 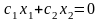) перпендикулярно вектору .

4. при решении задачи на максимум перемещают линию уровня 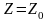в направлении вектора так, чтобы она касалась области допустимых значений в ее крайнем положении (если решается задача на минимум, то перемещают линию уровня в направлении антиградиента).

5. определяется оптимальный план 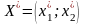и экстремальное значение функции .

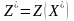При этом возможны следующие случаи:

1. оптимальный план единственный (на рисунке – точка B – максимум, точка O – минимум)

Пример 8: ,

b.оптимальных планов бесконечное множество, при этом линия уровня проходит по границе области допустимых значений (альтернативный оптимум)

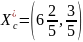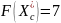
Пример 9: , , =1

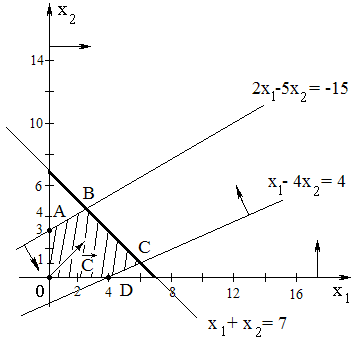
3. целевая функция не ограничена (С – точка минимума; максимума целевая функция не достигает в силу неограниченности ОДП).

Пример 10:

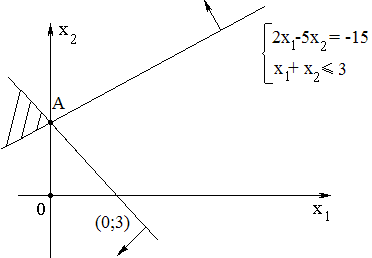
3. если область допустимых планов состоит из одной точки, то эта точка является решением ЗЛП.

4. если область допустимых планов – пустое множество – в этом случае задача не имеет решения.

Пример 11 (преобразование ЗЛП к каноническому виду и графическое решение)

ЗЛП сформулирова-на в общем виде (x, y – переменные)

границы области допустимых решений задаются уравнениями прямых «в отрезках»

ЗЛП сформулиро-ванная в каноническом виде

свободные переменные

Легко различить базисные и свободные переменные, составив матрицу A.

Свободные переменные

Базисные переменные

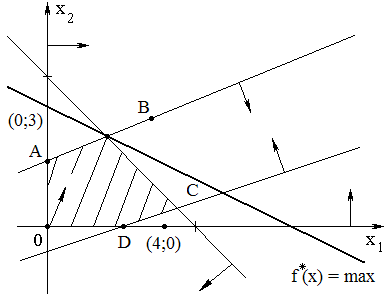
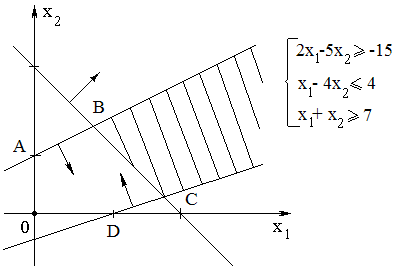
На плоскости 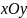построены полуплоскости, задаваемые ограничениями (2). Анализ чертежа показывает, что ограничение (e) – избыточное (его можно отбросить). Через точку C(6;1) проходит 3 прямые (a), (b), (d), что указывает на вырожденность соответствующего опорного решения (содержащего базисные 0). Получена область допустимых значений – выпуклый многоугольник ABCD.

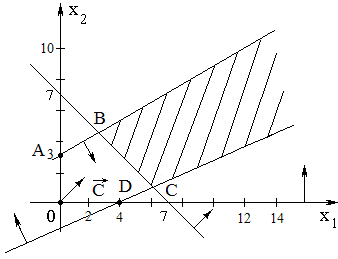
Из точки O(o,o) проведены векторы 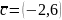- градиент и . Смещая линии уровня в направлении градиента, найдём точку в которой целевая функция достигает максимального значения. B(1;6) – план, обеспечивающий max f(x,y): .

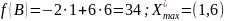Смещая линии уровня в направлении антиградиента, найдём точки в которой целевая функция достигает минимального значения. D(3;0), C(6;1) – планы, обеспечивающие min f(x,y) :

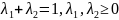
(на альтернативный оптимум указывает то, что анти градиент ортогонален одной из границ области G: отрезку CD)

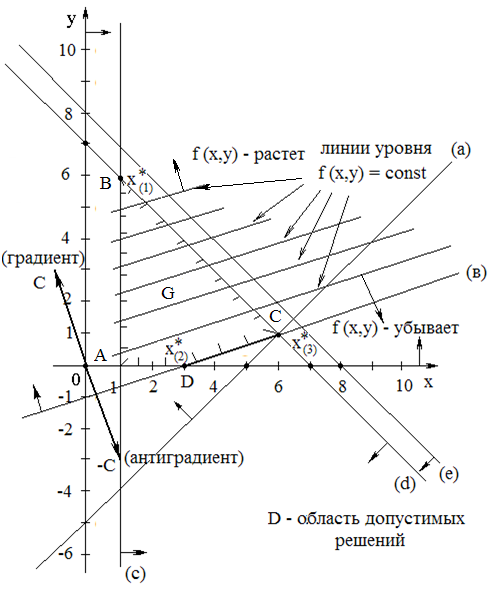
Рисунок 5. Графическое решение ЗЛП
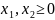
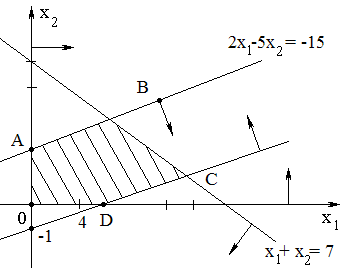
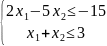
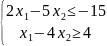