
- •Введение в исследование операций
- •Основные понятия
- •I раздел. Линейное программирование
- •П.1. Примеры постановки задач линейного программирования.
- •Задача о наилучшем использовании ресурсов.
- •Задача о смесях (о диете).
- •Задача о раскрое материалов
- •П.2. Основные понятия линейного программирования
- •Общий вид злп
- •П.4. Геометрическая интерпретация и графическое решение злп
- •Алгоритм графического решения злп.
- •П.5. Свойства решений злп.
- •П.6. Симплекс-метод решения злп
- •Теоремы о связи решения исходной злп и м-задачи.
Общий вид злп
(4)
 (5
a)
(5
a)
 (5
b)
(5
b)
 (5
c)
(5
c)
 (6
a)
(6
a)

 (6
b)
(6
b)
Правила перехода от ЗЛП в общем виде к ЗЛП в канонической (или симметричной) форме
|
|
||||||||||||
Свойства канонической (симметричной) формы ЗЛП |
Способ преобразования |
|
|||||||||||
свободные
члены неотрицательны
|
если свободный член в ограничении отрицательный – соответствующее выражение домножается на ( -1);
|
|
|||||||||||
знак ограничения-неравенства в симметричной ЗЛП не соответствует характеру оптимизации |
при
переходе к симметричной форме
неравенство
типа « |
|
|||||||||||
все
переменные неотрицательны
|
неотрицательности «свободных» переменных добиваются введением разности двух других неотрицательных переменных:
|
|
|||||||||||
все
ограничения (2)
–
равенства: « |
преобразуют ограничения- неравенства по правилу (таблица 1): таблица 1.
то есть ограничения – неравенства
преобразуются
в ограничения–равенства путем
прибавления (или вычитания) дополнительных
(балансовых) переменных
|
|
|||||||||||
чтобы
изменить характер оптимизации домножают
на ( -1) целевую функцию:
|
|
||||||||||||
Схема преобразования
|
ограничений-неравенств в равенства:
|
|
|
||||||||||
|
|
|
|||||||||||
|
|
не изменяется |
|||||||||||
Возможен также переход от канонической формы записи к общей. Для этого ограничения-равенства записывают в виде ограничений-неравенств. Затем отбрасывают базисные переменные, полученные с использованием преобразований Жордано - Гаусса и получают ограничения-неравенства.
Пример
1.
Привести к каноническому виду ЗЛП:


В
задаче общего вида нет условия
неотрицательности для переменной
 .
А
первые два ограничения системы не
являются равенствами. После преобразований
задача примет вид:
.
А
первые два ограничения системы не
являются равенствами. После преобразований
задача примет вид:


Пример
2.
Привести к симметрической ЗЛП:


Преобразуем матрицу системы ограничений используя метод Жордана-Гаусса:




После
подстановки
 в
целевую функцию и преобразования
ограничений в неравенства, получим:
в
целевую функцию и преобразования
ограничений в неравенства, получим:




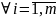
 »
умножением на (-1) преобразуется в
неравенство типа «
»
т, наоборот
»
умножением на (-1) преобразуется в
неравенство типа «
»
т, наоборот

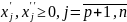
 »
»





 :
:
 т.е. вместо
т.е. вместо
 можно искать
можно искать








