
- •Введение в исследование операций
- •Основные понятия
- •I раздел. Линейное программирование
- •П.1. Примеры постановки задач линейного программирования.
- •Задача о наилучшем использовании ресурсов.
- •Задача о смесях (о диете).
- •Задача о раскрое материалов
- •П.2. Основные понятия линейного программирования
- •Общий вид злп
- •П.4. Геометрическая интерпретация и графическое решение злп
- •Алгоритм графического решения злп.
- •П.5. Свойства решений злп.
- •П.6. Симплекс-метод решения злп
- •Теоремы о связи решения исходной злп и м-задачи.
Введение в исследование операций
Учебное пособие ставит своей целью помочь в изучении способов построения математических моделей явлений и процессов различной природы, их анализе и прогнозировании на их основе. В нескольких главах рассмотрены основные задачи линейного и нелинейного программирования, основы матричных игр и сетевого планирования. Для продуктивного изучения курса необходимо знание линейной алгебры, математического анализа и теории вероятностей.
Основные понятия
Операцией называется – любое управляемое мероприятие, направленное на достижение цели. Ее результат зависит от выбора набора параметров (например, способа проведения). Всякий определенный набор параметров называется решением; оптимальным считают то решение, которое по тем или иным причинам предпочтительнее других.
Цель исследования операций – количественное обоснование принимаемых решений по организации управления.
Для получения количественных результатов необходимо построить математическую модель задачи (ММЗ), то есть отражение операции в виде функций, уравнений, неравенств, цифр и т.п. Математическая модель включает в себя:
совокупность переменных
 ,
действуя на которые (т.е. перебирая их
различные значения) оптимизируют
решение;
,
действуя на которые (т.е. перебирая их
различные значения) оптимизируют
решение;целевую функцию (иначе критерий оптимальности или функцию цели)
 (это может быть прибыль, издержки
обращения, затраты производства,
количество отходов и т.п.). Целевая
функция позволяет выбрать наилучший
вариант
(это может быть прибыль, издержки
обращения, затраты производства,
количество отходов и т.п.). Целевая
функция позволяет выбрать наилучший
вариант
 из множества возможных. Наилучший
вариант дает целевой функции экстремальное
значение
из множества возможных. Наилучший
вариант дает целевой функции экстремальное
значение
 ;
;систему ограничений (условия, налагаемые на неизвестные величины, которые задаются в виде неравенств и уравнений).
I раздел. Линейное программирование
Если
в математической модели целевая функция
и функции
 ,
входящие в систему ограничений, линейны
относительно
переменных
,
входящие в систему ограничений, линейны
относительно
переменных
 ,
то такой раздел исследования операций
называют линейным
программированием.
,
то такой раздел исследования операций
называют линейным
программированием.
П.1. Примеры постановки задач линейного программирования.
Задача о наилучшем использовании ресурсов.
Пусть
предприятие может выпускать n
различных
видов продукции

 .
Производство этих видов продукции
ограничено имеющимися
.
Производство этих видов продукции
ограничено имеющимися
 видами
ресурсов
видами
ресурсов

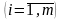 .
Запасы ресурсов ограничены и их количества
равны, соответственно:
.
Запасы ресурсов ограничены и их количества
равны, соответственно:
 .
.
Известна
экономическая выгода производства
продукции каждого вида (это может быть
отпускная цена товара, его прибыльность,
издержки производства). Пусть, например,
цена реализации равна .
.
Таким
образом, заданы
 - вектор
ресурсов
и
- вектор
ресурсов
и
 ,
- вектор
цен.
Известны также технологические
коэффициенты
,
- вектор
цен.
Известны также технологические
коэффициенты
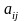 ,
которые показывают, сколько единиц i-го
ресурса требуется для производства
единицы продукции j-го
вида. Матрица
,
которые показывают, сколько единиц i-го
ресурса требуется для производства
единицы продукции j-го
вида. Матрица
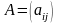 ,
которую они образуют - технологическая
матрица.
,
которую они образуют - технологическая
матрица.
Пусть
 ,
- план производства, показывающий, какие
виды товаров
и в каких количествах нужно производить,
чтобы обеспечить максимум объема
реализации при имеющихся ресурсах.
,
- план производства, показывающий, какие
виды товаров
и в каких количествах нужно производить,
чтобы обеспечить максимум объема
реализации при имеющихся ресурсах.
Модель
задачи имеет вид:


Задача о смесях (о диете).
Пусть имеется n различных видов продуктов . Требуется составить минимальный по стоимости рацион питания, удовлетворяющий требованиям питательности (содержать физиологически необходимое количество питательных веществ).
Известно
минимальное количество каждого из
 питательных
веществ (белки, углеводы, жиры и т.п.)
рациона
питательных
веществ (белки, углеводы, жиры и т.п.)
рациона
 и количество этих веществ в единице
питательного продукта
(злаки, молоко, рыба и т.п.) составляет
.
Стоимость единицы каждого продукта
равна
.
и количество этих веществ в единице
питательного продукта
(злаки, молоко, рыба и т.п.) составляет
.
Стоимость единицы каждого продукта
равна
.
Пусть , - количество продуктов , составляющих рацион, чтобы обеспечить минимум его стоимости при обеспечении необходимой питательности.
Модель
задачи имеет вид:


