1.Понятие предметноц области(ПрО).Объекты ПрО,их виды и свойства.Связи между объктами.

Предметная область-это часть реального мира,либо сфера деятельности человека,которая подлежит моделированию,т.е. изучению и использования для решения разлиных практических задач.сущность строения предметной области и её внешних факторов можно раскрыть с помощью таких категорий,как объек(сущность) с набором свойств и связей.Под объектом понимают некоторую сущность ПрО, о которой собирается информация и которая обрабатывается информ.системой.Объек может быть материальным(студенты например) и нематериальная(учебная десциплина,изуч.студентом например)

Каждый объек предсавляется своим уникальным именем и ед.числом.Уник.имя объекта называется индефикатором,кроме этого каждый объект обладает набором свойств(атрибутов)-характеристик.(цвеи,вес,размер и т.д),описывающих состояние каждой сущности .Свойство в задачах обработки информации также изменяют и придают им ещё значения.Экземпляром сущности является конкретный элемент её .Значение атрибута присваивается к конкретному экземпляру сущности.Совокупность однородных обьектов,т.е. Обьектов,обладающих одинаковым набором свойств и разл.их значениями называется классом(типом)обьектов.Чтобы отличать обьекты(экземпляры обьектов) друг от друна использутся понятие ключ(однозначно иденцифирующее обьект).кроме связи между обьектами и его свойствами.сущ связь между обьектами.связь-это ассоциация между сущностями,при которыз экземплятор одной сущности(записи)ассоциирован с произвольным кол-вом экземпляров(записей)другой сущности.выделяют след.типы связи:один к одному;один ко многим;многие к одному;многие ко многим.

2Понятие интуитивной и формальной модели ПрО.Многоуровневая система моделирования ПрО.

Процесс выделения информационных объектов предметной области, отвечающих требованиям нормализации, может производиться на основе интуитивного или формального подхода. Теоретические основы формального подхода разработаны известным американским ученым Дж. Мартином и изложены в его монографиях по организации баз данных. При интуитивном подходе легко выявить информационные объекты, соответствующие реальным объектам, однако получаемая при этом информационно-логическая модель, как правило, требует дальнейших преобразований, в частности преобразования много-многозначных связей между объектами. При таком подходе в случае отсутствия достаточного опыта возможны существенные ошибки. Последующая проверка выполнения требований нормализации обычно показывает необходимость уточнения информационных объектов. Рассмотрим формальные правила выделения информационных объектов:

-на основе описания предметной области выявить документы и их атрибуты, подлежащие хранению в базе данных;

• определить функциональные зависимости между атрибутами;

• выбрать все зависимые атрибуты и указать для каждого все его ключевые атрибуты, т. е. атрибуты, от которых он зависит;

• сгруппировать атрибуты, одинаково зависимые от ключевых атрибутов. (Полученные группы зависимых атрибутов вместе с их ключевыми атрибутами образуют информационные объекты.)

 

 3. Логико-семантическое описание ПрО в виде диаграмм объектов-связей.

Разработка концептуального уровня БД

Целью данного этапа является последовательная разработка концептуальной информационно—логической модели предметной области, отражающей логику информации предприятия и даталогической модели базы данных.

Инфологическая модель предметной области

Исходными данными для построения ИЛМ предметной области являются результаты анализа предметной области, представленные в виде описания классов объектов и связей между ними. Чаще всего ИЛМ предметной области представляют в терминах семантической модели данных, в виде ER — диаграммы предметной области. Необходимо отметить, что выявление в предметной области классов объектов, связей, описание и отображение их в диаграмме происходит параллельно.

Методологии построения ER—диаграмм

В настоящее время существуют разнообразные методологий (нотации) построения ER—модели.  1 Методология Питера Чена. В 1976 году Питером Ченом была предложена семантическая модель "сущность—связь" — ER—модель, которая в настоящее время стала самой распространенной. Соглашения, используемые при изображении диаграммы: — классы объектов отображаются прямоугольником, свойства эллипсами, связи ромбами; — уникальный идентификатор (первичный ключ) отображается в виде эллипса, обведенного двойной линией; — мощность связи «один» отображается линией, «много» — линией со стрелкой. Особенности этой методологии: — метод позволяет показать связь между двумя, тремя и более классами объектов (сущностями); — связь может иметь собственные атрибуты; — нет возможности отображения взаимоисключающих  связей и непереносимости связей; — взаимоисключающие связи неявно реализуются в виде супертипов и подтипов; — нельзя выразить опциональность атрибутов и связей. На рисунке 6 приведен пример фрагмента ER—диаграммы в методологии Питера Чена.

 

 

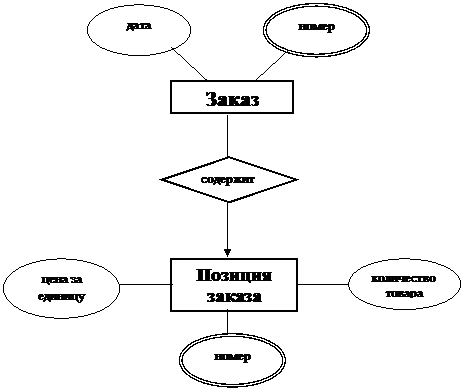
Рисунок 6 — Пример фрагмента ER—диаграммы в методологии Питера Чена

На диаграмме отображены следующие бизнес—правила предприятия: «Каждому заказу, имеющему такие свойства как номер и дата, должна соответствовать одна или более позиций заказа, имеющей такие свойства, как номер, цену за единицу товара, количество товара»; с другой стороны – «Каждая позиция товара должна относиться к одному и только одному заказу».  Необходимо отметить, что в примере приведен фрагмент описания предметной области. В ней также должны существовать такие классы объектов, как «Товар», «Единица измерения» и другие. 2 Методология IDEF1. Используется в CASE—средствах ERwin, Design/IDEF. В методологии используются следующие соглашения: — каждому классу объектов присваивается уникальное имя и номер; — обязательная связь отображается сплошной линией, необязательная – пунктирной;  — мощность связи "один" отображается линией, "много" – точкой; — связь может дополнительно определяться с помощью указания мощности (типа) связи. Мощность может принимать следующие значения: N – ноль, один или более (принимается по умолчанию); Z – ноль или один, P – один или более.  — свойства класса объектов отображаются в виде списка имен внутри блока, отображающего класс объектов; — атрибуты первичного ключа изображаются вверху и отделяются от других. Пример представления ER—диаграммы в методологии IDEF1 приведен на рисунке 7.

  Рисунок 7 — Пример представления ER—диаграммы в методологии IDEF1.

На рисунке 7 отображена та же ситуация в предметной области, что и на рисунке 6. 3 Методология Ричарда Баркера. Используемые в методологии элементы: класс объектов, свойство класса объектов, уникальные идентификаторы, опциональность свойств, связи, мощность (тип), опциональность и переносимость связей, уникальность объекта из связи, супертипы, подтипы, арки.  Используются следующие соглашения: — класс объектов отображается в виде четырехугольника с закругленными углами. Имя класса объектов указывается внутри четырехугольника, это имя существительное в единственном числе, отображенное заглавными буквами; — свойства записываются внутри четырехугольника, отображающего класс объектов строчными буквами, это имя существительное в единственном числе; — четырехугольник, отображающий класс объектов, можно увеличивать до любых размеров, четырехугольники могут быть разных размеров; — опциональность свойств помечается: обязательное свойство – звездочкой (*), необязательное – кружочком (о); — уникальный идентификатор помечается #, если уникальных идентификаторов несколько, тогда каждый помечается номером, указанным в скобках, например,  # (1), #(2); — обязательная связь помечается сплошной линией, необязательная – пунктирной; — тип (мощность) связи «один» помечается линией, «много» — «вороньей лапой». Более сложные элементы, используемые в ER—диаграмме, построенной по методологии Ричарда Баркера, рассмотрим далее в примерах.

4. Табличное задание отношений в реляционных БД. Особенности реляционных таблиц.

Реляционная база данных — это совокупность взаимосвязанных таблиц, каждая из которых содержит информацию об объектах определенного типа. Строка таблицы содержит данные об одном объекте (например, товаре, клиенте), а столбцы таблицы описывают различные характеристики этих объектов — атрибутов (например, наименование, код товара, сведения о клиенте). Записи, т. е. строки таблицы, имеют одинаковую структуру — они состоят из полей, хранящих атрибуты объекта. Каждое поле, т. е. столбец, описывает только одну характеристику объекта и имеет строго определенный тип данных. Все записи имеют одни и те же поля, только в них отображаются различные информационные свойства объекта.

В реляционной базе данных каждая таблица должна иметь первичный ключ — поле или комбинацию полей, которые единственным образом идентифицируют каждую строку таблицы. Если ключ состоит из нескольких полей, он называется составным. Ключ должен быть уникальным и однозначно определять запись. По значению ключа можно отыскать единственную запись. Ключи служат также для упорядочивания информации в БД.

Таблицы реляционной БД должны отвечать требованиям нормализации отношений. Нормализация отношений — это формальный аппарат ограничений на формирование таблиц, который позволяет устранить дублирование, обеспечивает непротиворечивость хранимых в базе данных, уменьшает трудозатраты на ведение базы данных.

Пусть создана таблица Студент, содержащая следу-рэщие поля: № группы, ФИО, № зачетки, дата рождения, шазвание специальности, название факультета. Такая организация хранения информации будет иметь ряд недостатков:

• дублирование информации (наименование специальности и факультета повторяются для каждого студента), следовательно, увеличится объем БД;

• процедура обновления информации в таблице затрудняется из-за необходимости редактирования каждой записи таблицы.

Нормализация таблиц предназначена для устранения этих недостатков. Имеется три нормальные формы отношений.

Первая нормальная форма. Реляционная таблица приведена к первой нормальной форме тогда и только тогда, когда ни одна из ее строк не содержит в любом своем поле более одного значения и ни одно из ее ключевых полей не пусто. Так, если из таблицы Студент требуется получать сведения по имени студента, то поле ФИО следует разбить на части Фамилия, Имя, Отчество.

Вторая нормальная форма. Реляционная таблица задана во второй нормальной форме, если она удовлетворяет требованиям первой нормальной формы и все ее поля, не входящие в первичный ключ, связаны полной функциональной зависимостью с первичным ключом. Чтобы привести таблицу ко второй нормальной форме, необходимо определить функциональную зависимость полей. Функциональная зависимость полей — это зависимость, при крторой в экземпляре информационного объекта определенному значению ключевого реквизита соответствует только одно значение описательного реквизита.

Третья нормальная форма. Таблица находится в третьей нормальной форме, если она удовлетворяет требованиям второй нормальной формы, ни одно из ее неключевых полей не зависит функционально от любого другого неключевого поля. Например, в таблице Студент (№ группы, ФИО, № зачетной книжки, Дата рождения, Староста) три поля — № зачетной книжки, № группы, Староста находятся в транзитивной зависимости. № группы зависит от № зачетной книжки, а Староста зависит от № группы. Для устранения транзитивной зависимости необходимо часть полей таблицы Студент перенести в другую таблицу Группа. Таблицы примут следующий вид: Студент (№ группы, ФИО, № зачетной книжки, Дата рождения), Группа (№ группы, Староста).

Над реляционными таблицами возможны следующие операции:

• Объединение таблиц с одинаковой структурой. Результат— общая таблица: сначала первая, затем вторая (конкатенация).

• Пересечение таблиц с одинаковой структурой. Результат — выбираются те записи, которые находятся в обеих таблицах.

• Вычитание таблиц с одинаковой структурой. Результат — выбираются те записи, которых нет в вычитаемом.

• Выборка (горизонтальное подмножество). Результат — выбираются записи, отвечающие определенным условиям.

• Проекция (вертикальное подмножество). Результат — отношение, содержащее часть полей из исходных таблиц.

• Декартово произведение двух таблиц Записи результирующей таблицы получаются путем объединения каждой записи первой таблицы с каждой записью другой таблицы.

Реляционные таблицы могут быть связаны друг с другом, следовательно, данные могут извлекаться одновременно из нескольких таблиц. Таблицы связываются между собой для того, чтобы в конечном счете уменьшить объем БД. Связь каждой пары таблиц обеспечивается при наличии в них одинаковых столбцов.

Существуют следующие типы информационных связей:

• один-к-одному;

• один-ко-многим;

• многие-ко-многим.

Связь один-к-одному предполагает, что одному атрибуту первой таблицы соответствует только один атрибут второй таблицы и наоборот.

Связь один-ко-многим предполагает, что одному атрибуту первой таблицы соответствует несколько атрибутов второй таблицы.

Связь многие-ко-многим предполагает, что одному атрибуту первой таблицы соответствует несколько атрибутов второй таблицы и наоборот.

5. Теоретико-множественные операции над реляционными таблицами реляционной БД и их применение для корректировки БД.

6. Операции проекции, выбора, соединения, деления над реляционными таблицами

Виды действий (манипуляций) над данными в реляционной модели представляют собой множество операций, получивших в совокупности название реляционной алгебры.

Каждая операция реляционной алгебры использует одно или два отношения в качестве операндов и создает в результате некоторое новое отношение. Э.Ф. Коддом были определены восемь таких опе­раций, объединенных в две группы по четыре операции в каждой.

Первая группа — традиционныетеоретико-множествен- ные операции (рис. 5.7).

Рис. 5.7. Диаграммы традиционных теоретико-множественных операций: а — объединение; б - пересечение; в — разность; г — декартово произведение

В каждой из этих операций используются два операнда (от­ношения). Для всех операций, кроме декартова произведения, эти два операнда должны быть совместимы по объединению, т.е. они

должны быть одной степени и их i-e атрибуты (I = 1,п) должны быть связаны с одним и тем же доменом.

Операция "объединение". Объединением двух отношений А и В называется множество всех кортежей принадлежащих либо отношению А, либо В, либо им обоим. Символически эта опера­ция показана на рис. 5.7, а. Математически операция объедине­ния записывается так:

А1)в= {гЛе А или г .В},

где и — символ объединения;

е — знак принадлежности определенному отношению (множеству).

Операция "пересечение". Пересечением двух отношений А и В называется множество всех кортежей г, каждый из которых при­надлежит как А, так и В (рис. 5.7,

АПб= {пг <А и г е. В], где П — символ пересечения.

Операция "разность". Разностью между двумя отношениями А и В называется множество всех кортежей каждый из которых принадлежит А и не принадлежит В (рис. 5.7,

А\В =

где \ — символ разности;

е — символ отсутствия принадлежности отношению (множеству).

Операция "декартово произведение". Декартовым произведе­нием двух отношений А Вназывается множество всех кортежей г, таких, что г является конкатенацией (соединение в цепочки) некоторого кортежа а, принадлежащего А, и какого-либо корте­жа принадлежащегоВ (рис. 5.7, г):

А х В= {ах, ау, Ъх, Ъу,сх, су, йх, йу}.

Вторая группа — специальные реляционные операции (рис. 5.8).

Операция "селекция". Пусть гкега представляет собой любой до­стижимый оператор сравнения скаляров, например =, >, >, < и т.д. 1Ъе1а-селекцией отношения А по атрибутам х и у называет­ся множество всех кортежей t из А, таких, что истин предикат t.x theta t.y.Атрибуты х и ^должны быть определены на одном и том же домене, и для этого домена оператор theta должен иметь смысл. Вместо атрибута у может быть задана константа (напри­мер, выбрать из платежной ведомости записи о сотрудниках, имеющих зарплату 500 руб.). Таким образом, оператор theta-ce- лекции позволит получать "горизонтальные" подмножества за­данного отношения, т.е. подмножества таких кортежей заданно­го отношения, для которых выполняется поставленное условие (см. рис. 5.8, а).

Операция "проекция". Она позволяет получить "вертикальное" подмножество заданного отношения, т.е. такое подмножество, которое получается выбором специфицированных (определенных) атрибутов с последующим исключением, если это необходимо, избыточных дубликатов кортежей, состоящих из значений выб­ранных атрибутов (см. рис. 5.8,

Рис, 5.8. Диаграммы специальных реляционных операций: а — селекция; б — проекция; в — соединение; г — деление

Операция "соединение"(рис. 5.8, в). Пусть theta имеет тот же смысл, что и в операции селекции. Тогда                                                                     отно­

шения А по атрибуту х с отношением В по атрибуту у называет­ся множество всех кортежей /, таких, что / является конкатенаци­ей какого-либо кортежа а, принадлежащего А, и какого-либо кор­тежа в, принадлежащего В, и предикат а.х theta ь.у. принимает значение "истина". При этом атрибуты А.х и В.у должны быть определены на одном и том же домене, а операторtheta должен иметь смысл для этого домена. Если оператор — theta-равенство, то соединение называется эквисоединением (лат. aequus — рав­ный). Из этого определения следует, что результат эквисоедине- ния должен включать два идентичных атрибута. Если один из этих атрибутов исключается, что соединение можно осуществить с по­мощью проекции, результат называется естественным соедине­нием. Под неуточненным термином "соединение" понимают ес­тественное соединение.

Операция "соединение" похожа на декартово произведение. Отличие состоит в том, что декартово произведение предполага­ет сцепление кортежа из отношения А с каждым корте­жем из В, а в операции "соединение" кортеж из отношения А сцепляется только с теми кортежами из В, для которых выполне­но условие а.х =

Операция "деление". В простейшей форме операция деления делит отношение степени два (делимое) на отношение степени один (делитель) и создает (продуцирует) результирующее отношение степени один (частное). Пусть делимое А имеет атрибуты х и у,а делитель В — атрибут у (см. рис. 5.8, г). Атрибуты Л.^ и В.у дол­жны быть определены на одном домене. Результатом деления А на В является отношение С с единственным атрибутомх, таким, что каждое значение х этого атрибута С.х появляется как значе­ние А.х, а пара значений (х,у) входит в А для всех значений у, входящих в В. Другими словами, кортеж включается в результи­рующее отношение С только в том случае, если его декартово произведение с отношением В содержит отношение А.

Из восьми рассмотренных нами реляционных операций пять являются базовыми. Это селекция, проекция, декартово произ­ведение, объединение и разность. Остальные три операции мо­гут быть определены через базовые. Например, естественное со­единение может быть выражено как проекция селекции декарто­ва произведения.

Назначение реляционной операции присваивания состоит в том, чтобы сохранить значение какого-либо алгебраического выражения.

Операции реляционной модели данных дают возможность произвольно манипулировать отношениями, позволяя обновлять БД, а также выбирать подмножества хранимых данных и пред­ставлять их в нужном виде. Таким образом, особенностями, оп­ределившими преимущества реляционной модели, являются:

♦      множество объектов реляционной модели БД однородно — структура БД определяется только в терминах отношений;

♦     основная единица обработки в операциях реляционной мо­дели не запись (как в сетевых и иерархических моделях), а множе­ство записей — отношение.

7. Суперпозиция реляционных операций в запросах к БД. Процедурные и декларативные средства обработки реляционных БД.