2.2. Классификация погрешностей измерений

Погрешности можно классифицировать по многим признакам.

По слагаемым измерения различают: погрешность воспроизведения единицы физической величины (погрешность меры), погрешность преобразования, погрешность сравнения, погрешность фиксации результата сравнения.

В зависимости от причины возникновения различают: методическую погрешность (от несовершенства метода измерения, во многих случаях эта погрешность поддается теоретическому расчету, для ее уменьшения часто приходится переходить к другому методу или алгоритму измерения), инструментальную (обусловлена погрешностями средств измерения), энергетическую (обусловлена потреблением средством измерения мощности от объекта исследования), погрешность выхода неинформативных параметров исследуемого сигнала за допустимые пределы, внешнюю погрешность (обусловлена условиями, в которых проводится эксперимент), субъективную (обусловлена неправильным выбором модели, несовершенством органов чувств экспериментатора, небрежностью, невниманием).

В зависимости от способа выражения различают две разновидности погрешностей измерения: абсолютную и относительную.

Абсолютная погрешность измерения – погрешность, выраженная в единицах измеряемой величины:

,

где А – результат измерения, А_о – истинное значение (на практике вместо истинного значения используется действительное значение А_д).

Относительная погрешность – отношение абсолютной погрешности измерения к истинному значению измеряемой величины:

. (2.1)

По закономерности проявления различают систематическую, случайную, грубую погрешности.

Грубые погрешности существенно повышают ожидаемую при данных условиях погрешность (следствие небрежности экспериментатора, неожиданных внешних воздействий и т.п.).

Систематическая погрешность – составляющая погрешности измерения, которая сохраняет постоянное значение или проявляется с определенной закономерностью при повторных измерениях одной и той же величины.

Систематическая погрешность, связанная с неправильным выбором методики измерений, может быть обнаружена при анализе условий проведения эксперимента, повторных измерениях той же величины другими методами или приборами и исключена в процессе подготовки эксперимента.

Составляющую систематической погрешности _и, связанную с измерением и обусловленную точностью прибора, исключить нельзя, поэтому при оценке погрешностей ее учитывают.

Случайная погрешность _сл – составляющая погрешности измерения, изменяющаяся случайным образом при повторных измерениях одной и той же величины. Она вызвана большим числом случайных причин, действие которых на каждое измерение различно и не может быть заранее учтено.

Таким образом, погрешность результата  включает в себя погрешность измерения _и и случайную погрешность _сл:

. (2.2)

2.3. Вычисление случайных погрешностей измерения

Наиболее полную характеристику погрешностей измерений дает дифференциальный закон распределения вероятностей погрешности. Для его определения вблизи конкретного значения А_д необходимо произвести многократные независимые измерения одной и той же величины А. В результате получается ряд значений измеряемой величины А₁, А₂, ... А_n. Этому ряду соответствует ряд погрешностей _i = A_i – A.

Затем строят гистограмму зависимости , где _i – выбранная ширина интервала по шкале , n_i – число значений погрешностей, попавших в этот интервал, N – общее число измерений (рис. 2.1).

Д ля построения гистограммы число измерений должно быть велико. Значение n_i для каждого интервала должно быть не меньше 5…10. Полученная гистограмма соответствует конкретному значению А_д.

Когда число измерений стремится к бесконечности,  – к нулю, величина р_i () стремится к функции плотности распределения вероятностей р(), которая может быть аппроксимирована аналитической функцией, называемой законом распределения вероятностей.

В различных измерительных устройствах законы распределения вероятностей различны. Преимущественно встречаются нормальные и равномерные распределения, а также распределение по закону арксинуса. Возможны и композиции этих законов.

Если на результаты измерений оказывает слабое влияние множество независимых факторов, то эта функция соответствует нормальному закону распределения.

Функция р() обладает следующими свойствами:

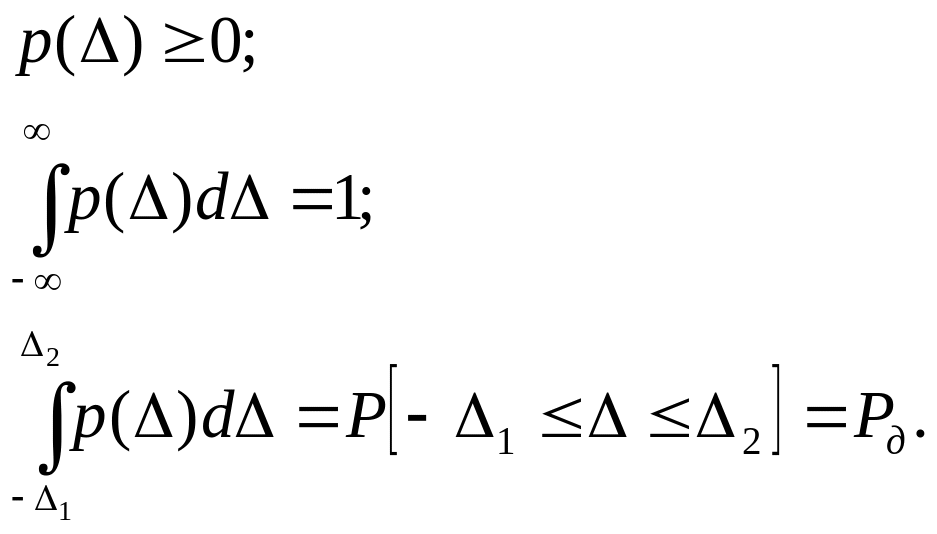
Наиболее важные числовые характеристики закона распределения – математическое ожидание _с (систематическая погрешность) и среднеквадратическое отклонение σ (или дисперсия σ ²):

;

.

Числовые вероятностные характеристики представляют собой неслучайные величины и теоретически определяются при бесконечном числе опытов. Практически число наблюдений всегда ограничено. Поэтому реально пользуются статистическими числовыми характеристиками, которые называют оценками и обозначают .

Оценка среднеквадратического отклонения (или S):

.

Оценка среднеквадратического отклонения среднего арифметического:

. (2.3)

Оценкой степени близости полученного и истинного значения измеряемой величины является доверительный интервал.

Зададимся положительными числами ₁ и ₂, имеющими размерность измеряемой величины. Обычно ₁ и ₂ выбирают существенно меньшими, чем измеряемая величина А, и равными друг другу. Интервалы А–₂ и А+₁ называют доверительными интервалами.

Вероятность того, что истинная величина А₀ окажется внутри этого интервала, называют доверительной вероятностью Р_д:

,

где Р – вероятность выполнения соответствующих неравенств.

Доверительная вероятность Р_д при заданном доверительном интервале является количественной мерой степени достоверности результата измерений.

Таблица 2.1