4. Базовые варианты задач

1 (31). Определить индикатрису силы излучения f(θ,φ) равнояркого непрозрачного параллелепипеда (рис. 4) с энергетичес­кой яркостью L_e и со сторонами a, b и с, выбрав направление фотометрической оси вдоль оси г. Найти локальные экстремумы функции f(θ,φ) в плоскостях xОz и yOz и ее глобальный экстремум. Определить поток излучения Ф_е, падающий от парал­лелепипеда на круг радиуса R = 3,2 м, параллельный плоско­сти xОу, Рис.4

центр которого находится на оси z на расстоянии l = 1,5 м от начала координат: α = 50 мм;

b = 80 мм; с = 100 мм; L_e = 100 Вт/(м² ср).

2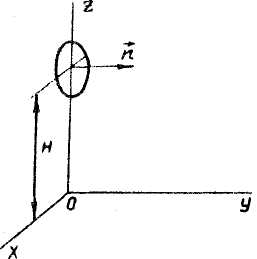 (32) Над плоскостью xOy (рис. 5) на высоте H находит­ся равнояркий диск яркостью L_v и диаметром D так, что нормаль к его плоскости параллельна оси Oу . Найти распределение освещенности в плоско-сти xОy , максимальную освещенность Е_тах и точку

В(x₀,y₀), в которой = Е_тах (H = 1 м;

L_v = 10³ кд/м²; D = 80 мм). Определить световой по- Рис. 5

ток, падающий на плоскость xOy.

3 (33). На расстоянии I от центра O равнояркого цилиндра с основанием радиуса r , высотой h и яркостью L_v находится круг, плоскость которого параллельна основанию цилиндра (рис. 6). Найти функцию распределения освещенности , где ρ - ра­диальная координата произвольной точки круга. Чему равен радиус круга R, если известно, что максимум функции приходит­ся на край круга? Найти световой поток Φ_v , падающий Рис. 6

на круг ( l = I м; r = 10 мм; h = 30 мм; L_v = Ι0³ кд/м²).

4 (34). Небольшой диффузно рассеивающий цилиндр с коэффици­ентом отражения поверхности ρ = 0,9, радиусом основания r и высотой h находится на расстоянии Η над плоскостью xOy и ориентирован так, что его ось параллельна оси Ох. Цилиндр освещается параллельным пучком лучей от точечного источника излучения силой I_e = 100 Вт/ср, находящегося на той же высоте и уда­ленного от цилиндра на расстояние I = 10 м вдоль оси Oy. Определять зависимость силы излучения цилиндра ( как вторичного Рис. 7

источника) от угла θ, лежащего в плоскости yOz, и облучен­ность Е_е в точке с(0,y) на плоскости xQy (рис. 7) ( r = 20 мм; h = 40 мм; Η = I м у₀ = 0,1 м).

5 (35). Нагретый цилиндр с основанием радиусом r = 15 мм и высотой h = 25 мм, находящийся на расстоянии Η от плоскости xOy (рис. 8), имеет зависимость спектрального коэффициента излучения от длины волны ε(λ) = 0,95 е^-λ, где λ - длина волны, мкм.

Определить температуру T цилиндра, если известно, что мо­нохроматическая освещенность от него в точке В(х₁,у₁) на длине волны λ₁ = 0,6 мкм и полосе Δ λ = 0,01 мкм равна Ε_v . Чему равна монохроматическая облученность Е_е в этой точке на длине волны λ₂ = 2λ₁, и полосе Δλ₂=Δλ₁

(x₁ = 0,2 м; у₁ = 0,8 м; H = 1м; E_v = 80 лк)? Рис. 8

6 (36). Определить температуру T равнояркого излучающего ци­линдра с основанием радиуса r = 15 мм и высотой h = 32 мм (см. рис. 8), если известно, что в точках В(х₁,у₁) и С(х₂,у₂) плоскости xОу, перпендикулярной к оси цилиндра и отстоящей на расстояние Η от его центра, монохроматические облученности Е_е(λ₁) и Е_е(λ₂) на длинах волн λ₁ и λ ₂= 2λ₁ в полосе Δλ = 0,01 мкм относятся между собой, как 1:4. Цилиндр счи­тать серым телом с коэффициентом излучения ε = 0,9. Чему рав­на освещенность Ε_v в точке В в полосе Δλ на длине волны λ_m, соответствующей максимальной спектральной плотности энергети­ческой светимоcти цилиндра (x₁ = I м; y₁ = I м; х₂ = 0,6 м; y₂ = 0,8 м; Η = I м; λ₁ = 0,4 мкм)?

7 (37). Определить температуру Τ равнояркого излучающего диска радиусом r, имеющего коэффициент излучениz ε = 0,9, если известно, что при изменении его температуры в 2 раза спектральная плотность энергетической яркости L_eλ диска на длине волны λ₁ возрастает в 5 раз. Чему равен поток Ф_е, из­лучаемый диском в телесный угол Ω ? Во сколько раз при том же изменении температуры диска изменится величина L_eλ на длине волны λ₂ , равной 0.5 λ_m , соответствующей температуре T? Какова максимальная сила света диска на длине волны λ₂ в полосе Δλ (­r = 80 мм; λ₁ = 2 мкм; Ώ = 1,5 ср; Δλ = 0,01мкм)?

8 (38). Нагретые шар и диск находятся на одной высоте H над плоскостью xОу (рис. 9), причем расстояние между их центрами равно b и плоскость диска параллельна плоскости xOy. Опре­делить температуру Т₂ диска, если температура шара Τ₁ = 3000 К и, кроме того, известно, что в точке Β(x₁,y₂) монохроматические облученности Е_е от шара и диска на длине волны λ₁ = 0.6 мкм в полосе Δ λ = 0,01 мкм одинаковы. Радиус шара r₁ = 10 мм, диска r₂ = 12 мм, а значения спектральных коэффициентов излучения на длине волны λ₁, для шара и диска соответственно равны ε₁(λ₁) = 0.8 и ε₁(λ₁) = 0.9. Найти монохроматическую освещенность Ε_v на длине волны λ₁, и полосе Δλ₁, в точке O плоcкости x0у ( H=1,2 м; b=0.8 м; x₁= 0; y₁ = 0,3 м).

Рис. 9