Линейные уравнения

Определение. Уравнение вида непрерывные функции, называется линейным дифференциальным уравнением первого порядка.

Если то уравнение называется линейным однородным уравнением.

Если то уравнение называется линейным неоднородным.

Для его решения применяют метод подстановки.

Пример 6. Найти общее решение уравнения .

Решение. Найдём общее решение данного уравнения методом подстановки.

Положим Подставляя эти выражения в данное уравнение, получим .

Потребуем, чтобы выражение в скобках обратилось в нуль, т.е. чтобы .

Подставляя найденное значение в уравнение , найдём Но .

Пример 7. Найти частное решение (интеграл) уравнения , если у(1)=2.

Решение. Это линейное уравнение первого порядка. Решим его методом Бернулли. Пусть . Подставляя в уравнение, имеем:

.

1) .

2) .

Отсюда получаем общее решение уравнения .

Учитывая условие у(1)=2, получаем: 2 = (1 + С), т.е. С = 1.

Частное решение исходного уравнения .

Уравнение Бернулли

Определение. Уравнение вида - непрерывные функции, называется уравнением Бернулли.

Уравнение Бернулли решается, также как и линейное, подстановкой

Пример 8. Решить уравнение .

Решение. Данное уравнение является уравнением Бернулли. Применим подстановку . Имеем . Или

. Откуда

1) .

2) .

Следовательно, решение уравнения .

Уравнение в полных дифференциалах

Определение. Уравнение вида называется уравнением в полных дифференциалах, если .

Если уравнение является уравнением в полных дифференциалах, то его можно представить в виде: . Откуда следует, что общее решение уравнения имеет вид .

Функция U(x,y) может быть найдена по формуле

,

где , в которой интегралы в правой части формулы имеют смысл.

Пример 9. Решить уравнение .

Решение. Это уравнение в полных дифференциалах. Здесь .

Значит, существует функция такая, что

Поэтому

Дифференцируя найденную функцию по у, получим выражение

Следовательно,

Пример 10. Найти общий интеграл уравнения

Решение. Здесь, т.е. данное уравнение является уравнением в полных дифференциалах.

Найдём общий интеграл по формуле .

Пусть , тогда

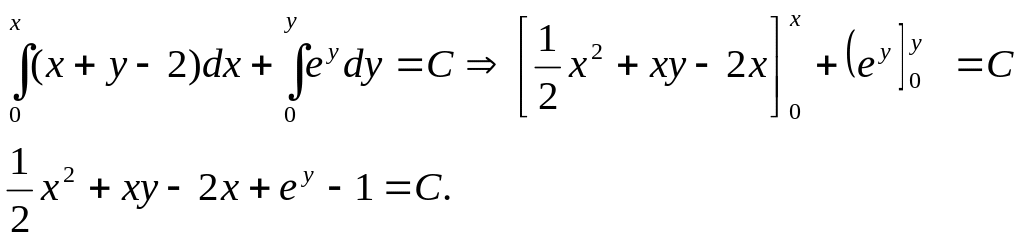
Пример 11. Решить уравнение

Решение. Уравнение в полных дифференциалах, так как . Вычислим

Беря все известные члены первого результата, и дописывая к ним недостающие члены, зависящие только от у, второго результата,

получаем общее решение исходного уравнения

Учитывая, что у(0)=0 имеем: С = 1. Следовательно, частный интеграл исходного уравнения .

Таким образом, чтобы решить уравнения первого порядка надо знать его вид и способ решения.

	Тип ДУ	вид	решение
1	с разделёнными переменными	или
2	с разделяющимися переменными
3	однородное	или
4	линейное
5	Бернулли
6	в полных дифференциалах

Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Определение. Уравнение вида где искомая функция, а и - вещественные числа, называется линейным однородным уравнением второго порядка с постоянными коэффициентами.

Теорема. Общее решение линейного однородного дифференциального уравнения имеет вид где линейно независимые решения этого уравнения.

Функции называются линейно независимыми на отрезке [a,b], если тождество

имеет место тогда и только тогда, когда

Теорема. Если линейно независимые на отрезке [a,b] решения дифференциального уравнения, то определитель Вронского этих функций отличен от нуля во всех точках этого отрезка [a,b],т.е.

Вронскиан не равен нулю ни в одной точке интервала (a;b) тогда и только тогда, когда частные решения линейно независимы.

Рассмотрим линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами

Квадратное уравнение называется характеристическим уравнением для уравнения (1).

Для составления общего решения дифференциального уравнения (1) необходимо найти корни соответствующего характеристического уравнения (2) и применить таблицу:

уравнение
характер. уравнение
дискриминант	корни	общее решение
D > 0
D < 0
D = 0

Пример 1. Найти общее решение уравнения .

Решение. Составляем характеристическое уравнение

Корни уравнения: действительные и различные. Общее решение имеет вид .

Пример 2. Найти общее решение уравнения .

Решение. Характеристическое уравнение имеет вид: .

Корни уравнения: действительные и равные. Общее решение уравнения имеет вид .

Пример 3. Найти общее решение уравнения .

Решение. Соответствующее характеристическое уравнение имеет вид

. Корни уравнения комплексные.

Общее решение уравнения имеет вид .

Пример 4. Найти общее решение уравнения .

Решение. Характеристическое уравнение имеет комплексные корни . Следовательно, общее решение уравнения имеет вид

.

Пример 5. Найти общее решение уравнения .

Решение. Характеристическое уравнение имеет различные действительные корни . Тогда общее решение уравнения имеет вид .

Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами.

Определение. Уравнение вида где вещественные числа, непрерывная функция, называется линейным неоднородным уравнением второго порядка с постоянными коэффициентами.

Уравнение, левая часть которого совпадает с левой частью неоднородного уравнения, называется соответствующим ему однородным уравнением.

Общее решение уравнения представляет собой сумму частного решения неоднородного уравнения и общего решения соответствующего однородного уравнения .

Рассмотрим один из методов нахождения частного решения линейного неоднородного уравнения.