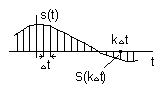Деңгейлік бойынша кванттау

Испульсті модуляция немесе кодтауды пайдаланумен байланыс жүйелері бойынша үзіліссіз хабартарды тасымалдау кезінде уақыт бойынша хабарты дискреттеу қажеттілігі туындайды. Соңғы уақытта үзіліссіз сигналдарды дискреттеу қажеттілігі кванттау әдісінің, сигналдар формасының дискретті анализімен, цифрлік және есептеу техникаларының дамуына түсіндіріледі.

Дисркттеу түсінігі s(t) функциясының уақыт бойынша үзіліссіздігі. Амплитуданың қысқа импульстері тізбегімен ауыстырылады, мұндағы ск (координаттар) жалпы жағдайда дискретті функция көмегімен анықталады:

x_к(t) .

Үзіліссіз функцияның оның дискретті координаттары бойынша туындауы базисті      функция жүйесі көмегімен жүргізіледі. Кейде салмақты және базисті функциялар бірдей қабылданады. Координатты функцияларды анықтау қиындығын ескере отыра, дискретті әдіс кең таралды, ондағы s(t) сигнал оның таңдама деп аталатын мәнінің жиынтығымен ауыстырылады. Бұл жағдайда салмақты (весовые) функция ролін d-функциясы ойнайды, Dt – дискреттеу қадамы (теңдестік болмауы мүмкін). .

Дәріс №9. Өзін-өзі тексеру сұрақтары немесе тесттер

1. Детерминделген сигналдар

2. Котельников теоремасы

3. Кванттау

Дәріс №10. АҚПАРАТТЫҚ ҮРДІСТЕР – АҚПАРАТТЫҚ ЖҮЙЕЛЕРІНІҢ НЕГІЗДЕРІ. ТАСЫМАЛДАУ ҮРДІСІНІҢ МОДЕЛІ.

• Ақпаратты өлшеу.

• Үзіліссіз және дискретті байланыс арналарының модельдері.

• Үзіліссіз және дискретті байланыс арналарының өту қабілеті.

Ақпаратты өлшеу

Ақпараттың саны, мәні мен бағалылығының түсінігі мағыналы болады, егер қарастыруда осы ақпаратты пайдаланатын жүйе – субъектісі пайда болса. Мұндай жүйе, мысалы қандайда бір агрегатпен басқаратын тірі ағза, адамдар қоғамы немесе компьютер болуы мүмкін.

Жүйе әрқашанда қандайда бір ортада жүреді. Өзінің есептерін шешу үшін оның өз ортасының моделі болуы керек және алынатын мәліметтер негізінде оларды түзетіп отыру керек.

Қандай да бір жағдай күтілсін, бастапқы мәні белгісіз болсын. n мүмкін бастапқы санға қатысты Н қандайда бір анықсыздық бар делік. Жағдай туындаған кезде, анықсыздық алынады және біз оның нақты бастапқы мәнін І ақпаратты аламыз.

Мысалы, ойын сүйегі (n = 6), немесе монета (n = 2) лақтырылады, n көлемді алфавиттен хабартар символы келіп түседі.

Жалпы жағдайда қандайда анықсыздық жағдай туындағаннан кейін сақталып (мысалы, алыстан сүйекте 4 немесе 6 түскенін айыру қиын) қалуы мүмкін.

Бұл жағдайда алынған ақпарат саны Нpr (априорды) тәжірибеге дейін және Нps (апостериорды) тәжірибеден кейін өлшем анықсыздығының айырымы теңестіріледі.

I = Нpr – Нps (1)

Егер тәжірибе көздерісы (Н_ps = 0) белгілі болса, онда I = Н_pr.

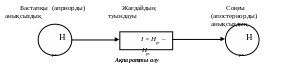Жағдай 1.1-суретте сипатталады.

1.1-сурет. Анықсыздық және ақпарат

L тәжірибе нәтижесінде мүмкін бастапқы мәндердің толық саны (хабартың l символының келіп түсуі) мынаны құрады:

Q = n^l (2.1)

Мысалы, ойын сүйектерінің екі лақтырылуының нәтижесі, 6² = 36 болуы мүмкін.

Н функциясын тәжірибе (мысалы, ойын сүйектерін үш рет лақтырған кезде анықсыздық бір рет лақтырғанға қарағанда үш есе көп) санына пропорционалды болатындай беру өте ыңғайлы. Мұндай құрам аддитивті деп аталады. Оған логарифмдік функция жауап береді

(2.2)

l =1 кезінде (ақпаратты беретін бір құбылыс немесе бір символ) мынаны аламыз

(2.3)

(2.3) формулада т мәніне өлшемнің әртүрлі бірліктері сәйкес келеді. Мысалы, т=е (натуралды логарифм) болғанда энтропия мен ақпарат «натта», m=1 болғанда - "дитте", т=2 болғанда – битте өлшенеді.

Бір бит элементарлы екілік таңдамаға сәйкес келеді.

(2.2) және (2.3) формулалар әртүрлі мәндердің теңсіздігінен шығады. Бұл жағдайда әрбір n бастапқы мәнінің р ықтималдығы бірдей.

Ойын сүйектерін немесе монеталарды лақтыру жағдайында бастапқы мәннің тең ықтималдылығы туралы ұсыныс дұрыс. Бірақ жалпы жағдайда n мүмкін бастапқы мәндер үшін p_i ықтималдығы әртүрлі. (2.2), (2.3) формулалар жеке (бірақ маңызды) жағдайға сәйкес, p_i барлық ықтималдығы және анықсыздығы максималды болғанда.

Бұл жағдайда (2.2) формула n бастапқы мәнімен L тәжірибе нәтижесінде алынған ақпараттың максималды мәнін сипаттайды (немесе n көлемді алфавиттен L символ ұзындығымен хабартар түскен кезде).

(2.2) - (2.3) формулалар ғалым Хартлимен ұсынылған және “харттілі” ақпарат санының өлшемі деп аталады. L мен n мәндері хабартың құрылымын (оның габаритін) анықтайтындықтан, сондай-ақ басқа термин: ақпараттың құрылымдық өлшемі пайдаланылады. Тәжірибеден кейін (хабартың символын алған кезде) анықсыздық жоқ болса, I = H ақпарат санын және (2.3) формуласын мына түрде жазуға болады

(2.4)