
- •Контрольная работа №1
- •Решить систему уравнений методом Крамера:
- •2. Провести исследование функции и построить ее график:
- •3. Найти кривизну линии в ее вершине. Начертить кривую и круг кривизны в ее вершине (только для «землеустройство и кадастры»)
- •Контрольная работа №2
- •4. Построить кривые и найти площадь, ограниченную двумя кривыми.
- •5. Найти частное решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами.
- •10. Непрерывные случайные величины. Нормальное распределение.
Контрольная работа №1
Решить систему уравнений методом Крамера:
вариант |
система уравнений |
вариант |
система уравнений |
1.1 |
3 -5x-2y+z=-9 -2x+3y+4z=4 |
1.6 |
3 x-y+4z=1 4x+2y+3z=8 4x-2y+2z=0
|
1.2 |
2 x-3y+3z=-4 -3x+y+2z=-1 5z-2y+z=1 |
1.7 |
4 x-y+3z=2 3x+2y+z=7 2x+3y+5z=8
|
1.3 |
- 3x+2y+z=1 -x-3y+2z=-7 -2x+y+4z=0 |
1.8 |
- 3x+y+2z=2 2x+y+z=0 x-2y+3z=-5
|
1.4 |
2 -3x+y+4z=-3 4x+3y+2z=1 |
1.9 |
- x-2y+3z=-5 2x+3y+z=2 4x-2y+5z=-7
|
1.5 |
x -4x+y+z=0 -3x+5y+4z=1 |
1.10 |
- 3x+y+z=0 2x+2y+3z=-1 5x-y+z=-2
|
2. Провести исследование функции и построить ее график:
вариант |
функция |
вариант |
функция |
2.1
|
y=4/3x3+x2-6x+1 |
2.6 |
y=-1/3x3+2x2+5x-1 |
2.2
|
y=-x3+3x2+9x-2 |
2.7 |
y=2x3-6x2-18x+4 |
2.3
|
y=3x3-4x+8 |
2.8 |
y=x3-3x2-9x+5 |
2.4
|
y=4x3-6x2+1 |
2.9 |
y=-x3+3x2+9x+4 |
2.5
|
y=x3-3x+2 |
2.10 |
y=1/3x3-x2-3x+5 |
3. Найти кривизну линии в ее вершине. Начертить кривую и круг кривизны в ее вершине (только для «землеустройство и кадастры»)
вариант |
уравнение линии |
вариант |
уравнение линии |
3.1
|
y=x2+9x-10 |
3.6 |
y=x2+2x-8 |
3.2
|
y=-x2+4x-3 |
3.7 |
y=-x2+2x+3 |
3.3
|
y=2x2-x-3 |
3.8 |
y=4x2+x-5 |
3.4
|
y=x2+2x-3 |
3.9 |
y=-3x2-x+4 |
3.5
|
y=2x2+3x-5 |
3.10 |
y=2x2+7x-9 |
Контрольная работа №2
4. Построить кривые и найти площадь, ограниченную двумя кривыми.
вариант |
1 кривая |
2 кривая (прямая) |
вариант |
1 кривая |
2 кривая (прямая) |
4.1
|
y=2x2-x-1 |
y= 2х + 1 |
4.6 |
y=2x2+x-3 |
y= 1 - х |
4.2
|
y=x2+x-2 |
y= 1 - х |
4.7 |
y=3x2-6x |
y= 3х |
4.3
|
y=x2-9 |
y= х + 3 |
4.8 |
y=2x2-2 |
y= 2х + 2 |
4.4
|
y=-x2-x + 6 |
y= -х - 3 |
4.9 |
y=3x2-7x+4 |
y= -2х + 4 |
4.5
|
y=x2-6x-7 |
y= х + 1 |
4.10 |
y=x2-4x |
y= х - 4 |
5. Найти частное решение линейного однородного дифференциального уравнения второго порядка с постоянными коэффициентами.
вариант |
диф. уравнение |
начальные условия |
вариант |
диф. уравнение |
начальные условия |
5.1
|
y”+10y’-11y=0 |
y(0)=-1,y’(0)=4 |
5.6 |
y”+16y=0 |
y(0)=3,y’(0)=-2 |
5.2
|
y”+25y=0 |
y(0)=1,y’(0)=2 |
5.7 |
4y”-15y’+14y=0 |
y(0)=-3,y’(0)=5 |
5.3
|
y”+9y’=0 |
y(0)=1,y’(0)=5 |
5.8 |
3y”-2y’-8y=0 |
y(0)=3,y’(0)=1 |
5.4
|
2y”+3y’-9y=0 |
y(0)=2,y’(0)=-3 |
5.9 |
y”-4 y’+3y=0 |
y(0)=-1,y’(0)=3 |
5.5
|
y”-8y’+7y=0 |
y(0)=1,y’(0)=-2 |
5.10 |
y”+8y’+12y=0 |
y(0)=-4,y’(0)=-5 |
6. Дана функция двух переменных z=f(x,y). Исследовать функцию на экстремум и найти градиент функции в точке М(x,y).
вариант |
уравнение функции, точка |
вариант |
уравнение функции, точка |
6.1 |
z=x2+y2-2x+2y+5, M(1;-1)
|
6.6 |
z=x2+y2-10x+2y+7, M(-1;2) |
6.2 |
z=x2+y2-4x-2y+1, M(2;-1)
|
6.7 |
z=x2+y2+2x-4y+8, M(-2; 1) |
6.3 |
z=x2+y2+6x-4y+3, M(-1;1)
|
6.8 |
z=x2+y2-4x-6y+2, M(1;-3) |
6.4 |
z=x2+y2-8x+2y-5, M(-2;-1)
|
6.9 |
z=x2+y2-6x+4y-3, M(1;3) |
6.5
|
z=x2+y2+4x-2y+6, M(1;1) |
6.10 |
z=x2+y2+8x+6y-4, M(2;-3) |
КОНТРОЛЬНАЯ РАБОТА №3
7. Классическое определение вероятности.
Теоремы сложения и умножения вероятностей
В группе 15 юношей и 8 девушек. Наудачу выбирают 3 дежурных. Какова вероятность, что все дежурные – юноши?
В корзине 5 красных и 2 зеленых яблока. Наудачу берут 3 яблока. Какова вероятность, что среди них одно яблоко зеленое?
В ящике 4 стандартных и 1 перегоревшая лампочка. Наудачу достают 3 лампочки. Какова вероятность, что среди них есть перегоревшая лампочка?
В коробке 10 конфет с темной и 3 со светлой начинкой. Наудачу достают две конфеты. Какова вероятность, что конфеты с разной начинкой?
В клетке 3 серых и 5 белых мышей. Наудачу достают 2 мыши. Какова вероятность, что мыши разного цвета?
В колоде 36 карт. Наудачу достают две карты. Какова вероятность, что обе карты одной масти?
Игральную кость подбрасывают 2 раза. Какова вероятность, что оба раза выпадет 3 очка?
В колоде 36 карт. Наудачу достают 4 карты. Какова вероятность, что все карты – тузы?
В ящике упакованы груши сорта А и сорта В, причем груш сорта А в 3 раза больше, чем сорта В. Наудачу взяли одну грушу. Какова вероятность, что взята груша сорта В?
7.10 На полке 5 книг по математике и 3 по истории расставлены в случайном порядке. Наудачу с полки снимают 2 книги. Какова вероятность, что обе книги по одной дисциплине?
8. Схема повторных независимых испытаний
Вероятность поражения мишени для данного стрелка составляет 0,8. Стрелок делает 6 выстрелов. Какова вероятность, что мишень будет поражена не менее 5 раз?
Приживаемость кустов роз составляет 0,6. Какова вероятность, что из 5 саженцев роз приживется хотя бы один саженец?
Какова вероятность того, что при 100 подбрасываниях игральной кости 6 очков выпадет ровно 30 раз?
На предприятии изделия высшего сорта составляют 15 %. Какова вероятность, что из 50 случайным образом отобранных деталей изделий высшего сорта будет не более 5 штук?
На основании многолетних наблюдений установлено, что на 1000 новорожденных приходится 512 мальчиков. Какова вероятность, что в семье из 5 детей не менее 4 мальчиков?
Данный стрелок в серии из 50 выстрелов сделал 40 попаданий. Какова вероятность, что при 100 выстрелах стрелок попадет не менее 90 раз?
Всхожесть семян данной культуры составляет 75%. Какова вероятность, что из 30 посеянных семян все 30 взойдут?
При тестировании студент решил выбирать ответ наудачу. Какова вероятность угадать правильный ответ на не менее 25 вопросов из 50, если на каждый вопрос дается на выбор три варианта ответа, из которых один правильный.
Дефект брошюровки книги составляет 0,0001. Какова вероятность, что из 5000 экземпляров дефект брошюровки будут иметь не более одной книги?
8.10 В результате проверки установлено, что для некоторой культуры из 100 семян 5 заражены болезнью в скрытой форме. Какова вероятность, что из 100 наудачу взятых семян болезнью в скрытой форме заражено не более 2?
9. Дискретные случайные величины и их числовые характеристики
вариант |
Закон распределения |
найти |
вариант |
Закон распределения |
найти |
||||||
9.1 |
хi |
-5 |
0 |
4 |
М(Х), Д(Х),
|
9.6 |
хi |
-6 |
0 |
2 |
М(Х), Д(Х),
|
pi |
0,5 |
0,2 |
… |
pi |
… |
0,4 |
0,2 |
||||
9.2 |
хi |
-3 |
0 |
2 |
М(Х), Д(Х),
|
9.7 |
хi |
-7 |
0 |
4 |
М(Х), Д(Х),
|
pi |
… |
0,1 |
0,4 |
pi |
0,6 |
… |
0,1 |
||||
9.3 |
хi |
-2 |
0 |
7 |
М(Х), Д(Х),
|
9.8 |
хi |
-8 |
0 |
5 |
М(Х), Д(Х),
|
pi |
0,3 |
… |
0,3 |
pi |
0,3 |
… |
0,1 |
||||
9.4 |
хi |
-6 |
0 |
10 |
М(Х), Д(Х),
|
9.9 |
хi |
-5 |
0 |
3 |
М(Х), Д(Х),
|
pi |
0.7 |
… |
0,1 |
pi |
0,4 |
… |
0,4 |
||||
9.5 |
хi |
-10 |
0 |
3 |
М(Х), Д(Х),
|
9.10 |
хi |
-9 |
0 |
1 |
М(Х), Д(Х),
|
pi |
… |
0,2 |
0,3 |
pi |
0,3 |
0,4 |
… |
||||

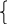 x-y+2z=1
x-y+2z=1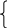 x-4y+z=5
x-4y+z=5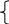 +3y+2z=1
+3y+2z=1