2 Раціональні підходи до конструювання
Можна виділити два підходи до конструювання на основі комп'ютерних технологій.
Перший підхід базується на двовимірній геометричній моделі і використовуванні комп'ютера як електронного кульмана, що дозволяє значно прискорити процес конструювання і поліпшити якість оформлення конструкторської документації.
Центральне місце в цьому підході до конструювання займає креслення, яке служить засобом представлення виробу, що містить інформацію для вирішення графічних задач, а також для виготовлення виробу (мал. 5).
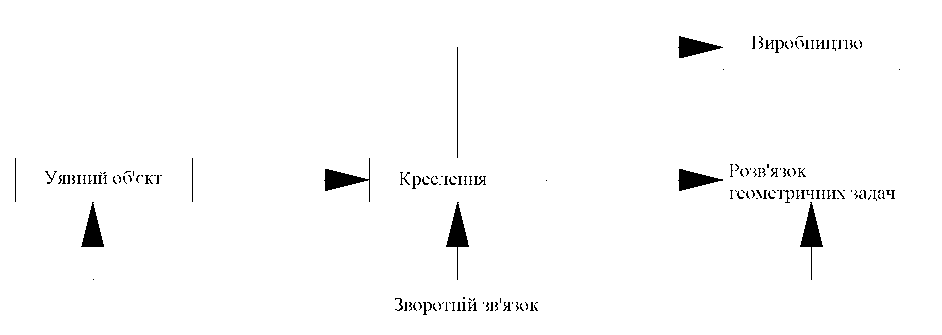
Малюнок 5. Схема традиційної технології конструювання
При такому підході отримання графічного зображення за комп'ютером буде раціональним і достатньо ефективним, якщо створене графічне зображення використовується багато разів.
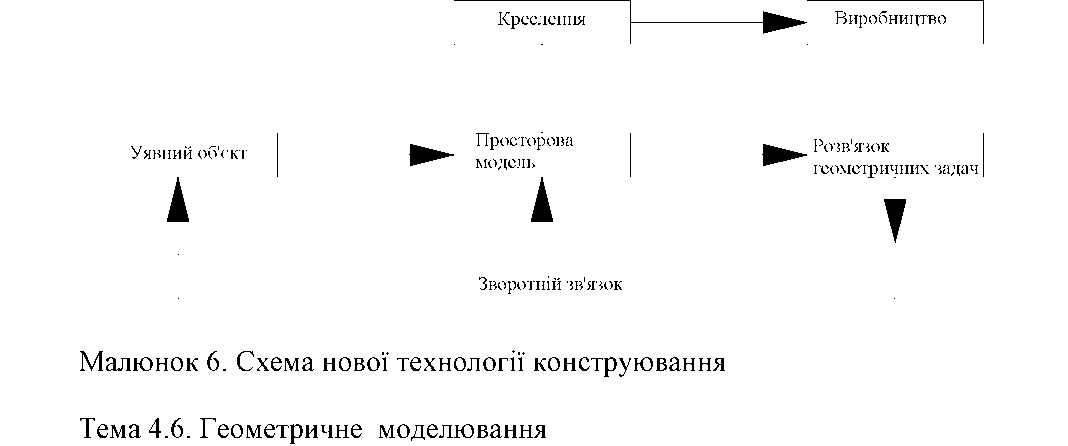
У основі іншого підходу лежить просторова геометрична модель виробу (мал. 6), яка є більш наочним способом представлення оригіналу і більш могутнім і зручним інструментом для вирішення геометричних задач.
Креслення в цих умовах грає допоміжну роль, а способи його створення засновані на методах комп'ютерної графіки, методах відображення просторової моделі.
При першому підході (традиційний процес конструювання) обмін інформацією здійснюється на основі конструкторської, нормативно-довідкової і технологічної документації; при другому - на основі машинного представлення геометричних об'єктів, загальної бази даних, що сприяє ефективному функціонуванню програмного забезпечення САПР конкретного виробу.
В процесі проектування використовують геометричне моделювання з відповідною організацією графічних даних. Під геометричним моделюванням розуміють створення моделей геометричних об'єктів, що містять інформацію про геометрію об'єкту.
Під моделлю геометричних об'єктів розумітимемо сукупність відомостей, що однозначно визначають його форму. Наприклад, точка може бути задана двома (двовимірна модель) або трьома (тривимірна модель) координатами; коло - координатами центру і радіусом і т.д.
Двовимірні моделі (графічних зображень) дозволяють формувати і змінювати креслення;
тривимірні моделі (просторова геометрична модель) - слугують для уявлення вироби в трьох вимірюваннях.
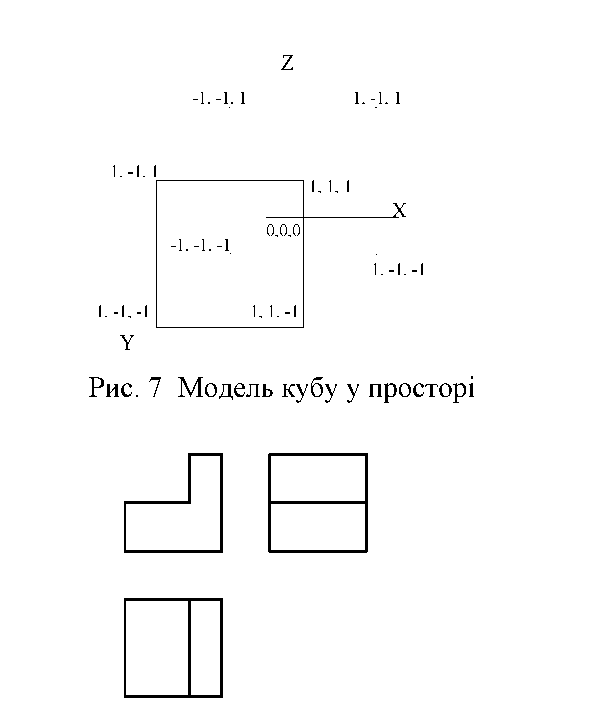
Засоби тривимірного моделювання. Будь-яка з проекцій ортогонального креслення (двомірна модель) розпізнається системою як плоский елемент, обмежений деякою кількістю крапок з певними координатами X і У. Просторова модель описується точками з третьою координатою по осі 2. На мал. 7 показана тривимірна модель куба.
На плоскому екрані (або кресленні) виходить лише уявний образ тривимірного куба, проте в пам'яті комп'ютера цей куб характеризується реальною тривимірною формою. Креслення фігури, показане на мал. 8, розпізнається двомірною системою як три повністю незалежних малюнка, обмежених загалом вісімнадцятьма точками.
Тривимірна система розпізнає їх як три проекції одного і того ж об'єкту, що має в просторі дванадцять вершин (мал. 9). І навіть, за умови що були представлено тільки два вигляди, наприклад Х2 і Х¥, то види ¥2 і Х¥2 можуть бути автоматично побудовані.
Малюнок 8. Ортогональне креслення фігури
Тривимірне моделювання ділиться на три вигляди:
каркасне;
поверхневе;
твердотільне (суцільне).
Слід відзначити, що системи, які приведені вище, володіють можливістю каркасного, поверхневого і твердотільного моделювання.
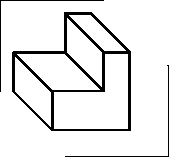
Малюнок 9. Розпізнавання тривимірною системою ортогонального креслення
Каркасне моделювання. - Каркасна модель повністю описується точками та лініями. Каркасне моделювання є моделюванням найнижчого рівня і має ряд суттєвих обмежень, більшість з яких виникає через нестачу інформації про грані, розташовані між ребрами, і неможливість виділити зовнішню і внутрішню області зображення, обмеженні можливості визначення які грані ми бачимо, які ні. Операцію по видаленню прихованих ліній можна виконати тільки уручну із застосуванням команд редагування до кожної окремої лінії.
Проте результат цієї роботи буде рівнозначний руйнуванню всієї створеної каркасної конструкції. Тому що лінії, видалені на одних проекціях, не зважаючи
на те, що вони видалені оскільки ми їх не бачимо автоматично будуть видалені її на решті проекцій.
Ще складніше йде справа з криволінійними поверхнями. Як відомо, циліндрова поверхня визначається переміщенням твірної по деякій спрямовуючій, тому в ортогональних проекціях така поверхня зображається за допомогою нарисових твірних, Природно, що ці твірні не є тотожними, наприклад, на головному вигляді і вигляді зліва, тому не розпізнаються як елементи каркасної моделі, а значить, і не зображаються на ній.
Поверхневе моделювання. Поверхнева модель визначається за допомогою точок, ліній і поверхонь. Таким чином, її можна розглядати як модель більш високого рівня, ніж каркасна модель, і, отже, як більш гнучку і багатофункціональну. Метод поверхневого моделювання найбільш ефективний при проектуванні складних криволінійних поверхонь, що виготовляються з листового матеріалу, наприклад, елементів кузова автомобіля.
Поверхні утворюються різними способами і можуть бути розділені для цілей комп'ютерної графіки за способом їх отримання на елементарні геометричні поверхні. До них відносять поверхні обертання, аналітичні поверхні і поверхні довільних форм (відомі також як «скульптурні» поверхні або поверхні «вільних форм»).
До елементарних геометричних поверхонь відносяться поверхні, які утворюються паралельним перенесенням лінії уздовж перпендикулярної до неї осі. Поверхні обертання можуть бути легко одержані обертанням деякої плоскої фігури навкруги певної осі Не дивлячись на цілий ряд переваг методу поверхневого моделювання, його вживання обмежено через ряд недоліків і, перш за все, через складність процедури видалення невидимих ліній і відображення внутрішніх областей.
Твердотільна модель описується в термінах того тривимірного об'єму, який займає це тіло. Таким чином, твердотільне моделювання є єдиним засобом, який забезпечує повний і однозначний опис тривимірної геометричної форми. Цей спосіб моделювання є найсучаснішим і наймогутнішим з трьох вказаних методів.
Незаперечними перевагами твердотільної моделі є:
повне визначення об'єму і форми;
забезпечення автоматичного видалення невидимих (прихованих) ліній;
автоматизована побудова тривимірних розрізів проектованого виробу, щоособливо важливе при аналізі складних складальних одиниць;
автоматичне отримання точних значень маси, площі поверхні, центру тяжкості, моменту інерції для будь-якої деталі або виробу у цілому;
підвищення ефективності імітації руху інструменту або робочих органів виробу;
наявність різноманітної палітри кольорів, управління колірної гаммою, отримання тонових ефектів - всього того, що сприяє отриманню якісного зображення форми.
Один з методів твердотільного конструювання заснований на побудові моделі з набору базових твердотільних примітивів, що знаходяться в бібліотеках системи. Кожний примітив визначений деякою формою (куля,циліндр змінного перетину, паралелепіпед і т. п.), точкою прив'язки, початковою орієнтацією і змінними розмірами.
Процес створення конструкції заснований на використовуванні булевих операцій. Булеві операції базуються на поняттях теорії алгебри множин. Розглянемо здійснення цих операцій на прикладі геометричних фігур кола А та прямокутника В (рис. 10 )
Рисунок 10
Операція об'єднання (У) визначає простір усередині зовнішньої межі складової фігури, одержаної з двох тел. Результат об'єднання двох довільних об’єктів А і В є заштрихованою областю А У В. Таким чином, операція об'єднання визначає результат складену фігуру як один елемент (рис. 11 ).
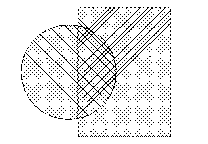
Малюнок 11. Графічна інтерпретація операція об'єднання А У В
Операція різниці (-) визначає простір, що залишився від однієї фігури після вирахування загальної області двох фігур. Тобто А-В є безліч точок, що належать А, але не належать В (рис. 12 ).
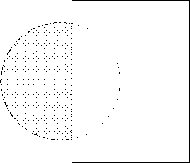
Малюнок 12. Графічна інтерпретація операції віднімання А-В
Операція перетину (П) визначає простір усередині меж загальної області фігур - безліч точок, що належать обом фігурам (рис. 13).
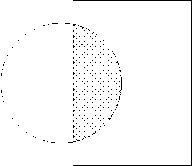
Малюнок 13 Графічна інтерпретація операції перетину А П В
Після створення повної тривимірної моделі можна виконати креслення даного виробу в ортогональних проекціях. Зробити це дозволяють програмні засоби автоматичного отримання необхідних проекцій з автоматичним же нанесенням розмірів на відповідні зображення.
На першому етапі реальний об'єкт, наприклад, деталь піддається абстракції, в результаті якої визначається інформаційна модель.
На другому етапі в інформаційній моделі виділяють рівні з урахуванням процесів обробки інформації в задачі проектування. Таким чином, здійснюється уточнення і структуризація інформації з логічної точки зору. Істотним моментом в цьому уявленні є те, що воно повинне відображати характеристики не однієї деталі, а цілого класу деталей на різних стадіях проектування, що фіксуються в технічній документації. При формуванні інформаційної моделі передбачається використовування безлічі конструктивних елементів для отримання деталей довільної форми, геометричних елементів (контурів, поверхонь, елементарних і складних об'єктів), які забезпечують обробку геометричної інформації для всіх процесів автоматизованого проектування. Таким чином, будується модель даних, яка відображає логічну структуру даних.
На третьому етапі здійснюється процес відображення моделі даних у внутрішньомашинне уявлення - формування моделі доступу. Модель доступу (або розміщення) орієнтована на фізичне розміщення даних в пам'яті ЕОМ, в моделі зберігання.
Таким чином, на четвертому етапі визначається модель зберігання, яка задає відображення даних, заданих в моделі доступу, на фізичну пам'ять і управління ними. Існують три способи організації даних на фізичних носіях: послідовний, списковий і прямий.
У AutoCAD, наприклад, використовується списковий спосіб зберігання геометричних даних, що дає можливість користувачу берегти дані на фізичних носіях незалежно від їх логічної послідовності.