
- •Лабораторная работа № 10 Гидравлический расчёт трубопроводов
- •Теоретическое введение
- •Вопросы для самопроверки
- •Задание
- •Требования к отчёту
- •Постановка задачи
- •Теоретические основы расчёта
- •Расчётная часть
- •Рекомендуемая литература
- •Приложения Приложение 1
- •Приложение 2
- •Зависимость плотности воды от температуры
- •Зависимость динамического коэффициента вязкости воды от температуры
- •Зависимость плотности и кинематического коэффициента вязкости некоторых жидкостей от температуры
- •Механические свойства труб
- •Приложение 10
- •Рекомендуемые диаметры труб для перекачки жидкостей с производительностью q
- •Сортамент труб
Лабораторная работа № 10 Гидравлический расчёт трубопроводов
Цель работы: изучение и практическое усвоение методики гидравлического расчёта простого напорного трубопровода, приобретение навыков работы с технической и справочной литературой
Теоретическое введение
При гидравлических расчетах рассматривается несколько видов трубопроводов.
К коротким трубопроводам относятся все трубопроводы, в которых местные потери напора превышают 5…10% потерь напора по длине. При расчетах таких трубопроводов обязательно учитывают потери напора в местных сопротивлениях. К ним относят, к примеру, маслопроводы объемных передач.
К длинным трубопроводам относятся трубопроводы, в которых местные потери меньше 5…10% потерь напора по длине. Их расчет ведется без учета местных потерь или потери учитывают через суммарную эквивалентную длину ℓэкв, обычно составляющую 1- 5% от реальной длины трубопровода. К таким трубопроводам относятся, например, магистральные водоводы, нефтепроводы и продуктопроводы.
Простые трубопроводы – это трубопроводы с постоянным диаметром, которые не содержат разветвлений. Трубопровод, содержащий как последовательные, так и параллельные соединения труб или разветвлений, называется сложным. Если сложный трубопровод имеет несколько труб, выходящих из одного места, он называется разветвленным.
Гидравлический расчет трубопроводов обычно сводится к определению одной из трех величин при заданных других:
напора H (или избыточного давления pи) при известных расходе Q жидкости, диаметре d и длине трубопровода l;
расхода Q жидкости при известных диаметре d трубопровода, его длине l и напоре H (или избыточного давления pи);
диаметра трубопровода d при заданных расходе Q жидкости и напоре H (или избыточного давления pи).
Основным уравнением, применяемым при расчете простых трубопроводов, является уравнение Бернулли.
Для двух сечений потока 1-1 и 2-2 реальной жидкости при установившемся движении уравнение Бернулли имеет вид
 ,
(1)
,
(1)
где
 и
и
 -
геометрический напор (удельная
потенциальная энергия положения) в
сечениях 1-1 и 2-2, м;
-
геометрический напор (удельная
потенциальная энергия положения) в
сечениях 1-1 и 2-2, м;
 и
и - пьезометрический
напор (удельная потенциальная энергия
давления ) в сечениях, м;
- пьезометрический
напор (удельная потенциальная энергия
давления ) в сечениях, м;
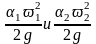 – скоростной напор
(удельная кинетическая энергия ) в
сечениях, м;
– скоростной напор
(удельная кинетическая энергия ) в
сечениях, м;
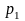 ,
, -
абсолютное давление в сечениях, Па;
-
абсолютное давление в сечениях, Па;
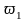 ,
, -
средние по живому сечению трубы скорости
потока в сечениях,
м/с;
-
средние по живому сечению трубы скорости
потока в сечениях,
м/с;
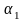
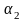 -
коэффициенты кинетической энергии
(коэффициенты Кориолиса) в сечениях;
-
коэффициенты кинетической энергии
(коэффициенты Кориолиса) в сечениях;
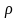 -
плотность жидкости, кг/м3;
-
плотность жидкости, кг/м3;
 -
потери напора в трубе между сечениями,
м.
-
потери напора в трубе между сечениями,
м.
Коэффициент
кинетической энергии
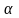 учитывает
неравномерность поля скоростей в
рассматриваемом живом сечении. Величина
коэффициента зависит от режима течения
жидкости: для ламинарного течения
=2;
для турбулентного течения
=1,05-1,15
(обычно
принимают
учитывает
неравномерность поля скоростей в
рассматриваемом живом сечении. Величина
коэффициента зависит от режима течения
жидкости: для ламинарного течения
=2;
для турбулентного течения
=1,05-1,15
(обычно
принимают
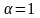 ).
).
Все члены уравнения Бернулли в формуле (1.1) имеют линейную размерность и в энергетическом смысле представляют удельную энергию жидкости, т.е. энергию, отнесенную к единице веса жидкости.
Сумма всех трех
членов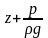 +
+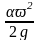 =H
представляет
собой полный напор в соответствующем
сечении.
=H
представляет
собой полный напор в соответствующем
сечении.
При расчете простых трубопроводов вместе с уравнением Бернулли применяется также уравнение неразрывности потока, т.е. равенства расхода во всех сечениях установившегося потока:
 .
(2)
.
(2)
Потери напора (удельной энергии), или гидравлические потери, разделяют на потери на трение по длине трубы и местные потери
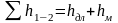 .
(3)
.
(3)
Потери на трение
по длине
 -
это потери
энергии, которые возникают в прямых
трубах постоянного сечения из-за трения
о стенки и между слоями жидкости
(внутреннего трением жидкости в трубах)
и возрастают прямо пропорционально
длине трубы.
-
это потери
энергии, которые возникают в прямых
трубах постоянного сечения из-за трения
о стенки и между слоями жидкости
(внутреннего трением жидкости в трубах)
и возрастают прямо пропорционально
длине трубы.
В инженерных расчётах они определяются по формуле Дарси-Вейсбаха соответственно через среднюю скорость или через расход жидкости:
 , (4)
, (4)
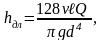 (5)
(5)
где λ – коэффициент гидравлического трения по длине, или коэффициент Дарси;
l – длина трубопровода, м.
Для
ламинарного
режима
движения
жидкости в круглой трубе коэффициент
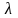 определяется по теоретической формуле
определяется по теоретической формуле
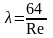 ,
(6)
,
(6)
где
 число Рейнольдса.
число Рейнольдса.
Для труб круглого сечения число Рейнольдса определяется по формуле
 ,
(7)
,
(7)
где
 - кинематический коэффициент вязкости
жидкости, м2/с.
- кинематический коэффициент вязкости
жидкости, м2/с.
При турбулентном режиме движения коэффициент λ зависит как от числа Рейнольдса, так и от относительной шероховатости поверхности стенок трубы ∆э/d (∆э - эквивалентная шероховатость, характеризующая высоту выступов шероховатостей труб, м), и определяется по эмпирическим формулам. При этом, как показано в опытах И.И. Никурадзе, при турбулентном режиме существует три области гидравлического трения:
область гидравлически гладких труб, где λ = f(Re);
область доквадратичного сопротивления или переходная, где λ = f(Re, Δэ/d);
область квадратичного сопротивления – автомодельности, где λ = f(Δэ/d).
М
еханизм гидравлического трения в каждой из этих областей зависит от соотношения размеров ламинарного подслоя толщиной δ и размеров шероховатости внутренней поверхности канала Δ (рис. 1.).

Рис. 1. Схема гидравлического трения при турбулентном режиме движения жидкости
В области гидравлически гладких труб δ > Δ. Поэтому вязкий подслой покрывает выступы шероховатости, и турбулентное ядро потока не взаимодействует с шероховатостью.
В области доквадратичного сопротивления (δ ≈ Δ) происходит постепенное «раскрывание» шероховатости турбулентным ядром. Здесь имеет место общий случай зависимости λ = f(Re, Δ/d). И, наконец, в области квадратичного сопротивления, когда выступы полностью «раскрыты», λ зависит только от размеров шероховатости.
На практике при инженерном расчете трубопроводов границы областей гидравлического трения определяют в зависимости от предельных чисел Рейнольдса:
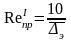 ,
,
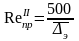 .
.
Если
Reкр<Re<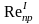 ,
имеем область гидравлически гладких
труб. Для расчета коэффициента
гидравлического трения рекомендуется
формула
Блазиуса:
,
имеем область гидравлически гладких
труб. Для расчета коэффициента
гидравлического трения рекомендуется
формула
Блазиуса:
λ = 0,3164/Re0,25. (8)
Если
<Re<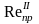 ,
имеем область доквадратичного
сопротивления или шероховатых труб.
Для
расчета коэффициента λ
рекомендуется формула
Альтшуля:
,
имеем область доквадратичного
сопротивления или шероховатых труб.
Для
расчета коэффициента λ
рекомендуется формула
Альтшуля:
λ= 0,11∙(68/Re + Δэ/d)0,25. (9)
Если Re> , имеем область вполне шероховатых труб или квадратичного сопротивления. Рекомендуется формула Шифринсона:
λ = 0,11∙(Δэ/d)0,25. (10)
Наиболее универсальной и удобной для расчета является формула Альтшуля, которая дает хорошие результаты для всего диапазона чисел Рейнольдса при турбулентном режиме.
Необходимое для расчёта значение эквивалентной шероховатости ∆э выбирают по справочным данным в зависимости от материала труб.
Местные потери энергии обусловлены так называемыми местными гидравлическими сопротивлениями, т.е. местными изменениями формы и размеров русла, вызывающими деформацию потока с интенсивным вихреобразованием.
Местные потери напора определяются по формуле Вейсбаха:
 , (11)
, (11)
где
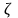 – коэффициент местного сопротивления.
– коэффициент местного сопротивления.
Значение коэффициентов местных сопротивлений можно ориентировочно определить по справочным данным в зависимости от вида (конструктивного оформления) сопротивления или в некоторых случаях рассчитать по теоретическим или эмпирическим формулам.
Общие потери напора в простом трубопроводе обычно рассчитывают с использованием принципа наложения (сложения) потерь:
 (
12 )
(
12 )
Таким образом, расчёт простых трубопроводов основан на применении уравнения Бернулли (1) и уравнения неразрывности потока (2). При этом целесообразно руководствоваться следующим:
- уравнение Бернулли составлять для двух живых сечений потока, нормальных к направлению скорости;
- живые сечения выбирать в начале и в конце рассматриваемой гидравлической системы и нумеровать по направлению движения жидкости;
- плоскость сравнения должна быть горизонтальной и проходить через центр тяжести живого сечения, расположенного ниже;
- для выбранных сечений записывают уравнение Бернулли в общем виде, а затем упрощают его с учетом заданных величин;
- если живое сечение совпадает со свободной поверхностью жидкости, а его площадь значительно больше площади сечения трубопровода, то скорость жидкости в этом живом сечении принимается равной нулю;
- в трубопроводах все потери энергии суммируются от начального (первого) к конечному (второму) живому сечению;
- полученное после всех преобразований и упрощений уравнение Бернулли совместно с уравнением неразрывности решается относительно неизвестной величины. При этом, если необходимо определить расход жидкости Q или диаметра трубопровода d, то расчётное уравнение оказывается трансцендентным и не решается алгебраическими методами. Для преодоления этой трудности существуют два способа – аналитический метод последовательных приближений и графоаналитический метод, использующий построения графических зависимостей.
Если в трубопроводе необходимо обеспечить расход жидкости Q, то потребный для этого напор Нпотр - пьезометрическая высота в начальном сечении p1/ρg - определится по формуле:
 (13)
(13)
где ∑h – суммарные потери напора на сопротивление в трубопроводе;
Нст – статический напор, включающий геометрическую высоту ∆z, на которую необходимо поднять жидкость в процессе ее движения по трубопроводу, и пьезометрическую высоту в конечном сечении трубопровода p2/ρg, т.е.
Нст =∆z+ p2/ρg (14).
При последовательном соединении участков сложного трубопровода справедливы равенства
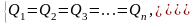 (15)
(15)
При параллельном соединении трубопроводов:
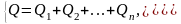 (16)
(16)
где Q – расход в точке разветвления;
п – количество разветвлений.
На равенствах (15) и (16) основывается способ построения характеристик сложных трубопроводов, состоящих из последовательных и параллельных соединений простых трубопроводов. Для того чтобы построить характеристику потребного напора сложного трубопровода, целесообразно:
– представить трубопровод в виде соединения простых участков;
– рассчитать и построить характеристики каждого простого участка трубопровода;
– провести графическое сложение характеристик параллельных участков;
– провести графическое сложение последовательных участков.
Если подача жидкости по трубопроводу осуществляется насосом с заданной характеристикой, то принцип расчета такого трубопровода заключается в совместном построении в координатах Н–Q линии потребного напора трубопровода и характеристики насоса. Точка пересечения этих линий (рабочая точка) соответствует рабочему режиму. Изменить расход жидкости в трубопроводе можно двумя способами: изменяя характеристику сети при неизменной характеристике насоса или изменяя характеристику насоса при неизменной характеристике сети.
