1.А. Определение курсовой стоимости среднесрочной и долгосрочной бескупонных облигаций.

Формулу определения курсовой стоимости бескупонной облигации можно получить из формулы (5.16). Поскольку по облигации не выплачиваются купоны, то С = 0 и формула (5.16) принимает вид:

(5.18)

Пример 5.3. N - 10000 руб., r - 20%, n - 3 года. Определить Р.

Если по облигации остается не целое число лет, то формула (5.18) примет вид:

(5.19)

Где: - число дней от момента сделки до начала целого годового периода для облигации;

n – целое число лет, которое остается до погашения облигации, включая текущий год.

На практике приходится сравнивать купонные и бескупонные облигации. В этом случае необходимо помнить о следующем правиле. Если по купонным облигациям процент выплачивается m раз в год, то формулу (5.18) следует также скорректировать на m, а именно:

(5.20)

2.А. Определение курсовой стоимости гко.

Цена ГКО определяется по формуле:

(5.21)

Где: N- номинал ГКО;

r - доходность до погашения;

t - количество дней от момента сделки до погашения ГКО.

Пример 5.4. N - 1 млн. руб., t - 60 дней, r - 15%. Определить цену ГКО. Она равна:

3.А. Определение курсовой стоимости офзпк и огсз.

Цена данных облигаций определяется стандартным способом, т. е. будущие доходы по облигациям дисконтируются к сегодняшнему дню и суммируются. Особенностью ОФЗ-ПК и ОГСЗ является то, что купоны у них плавающие и их величина изменяется в зависимости от ситуации на рынке ГКО. Поэтому инвестору необходимо вначале сделать прогноз относительно ситуации на рынке ГКО. Затем оценить величину будущих купонов и дисконтировать их и номинал к сегодняшнему дню.

Мы рассмотрели формулы определения курсовой стоимости облигаций. Они позволяют инвестору рассчитать приемлемый для него уровень цены бумаги. В то же время это не означает, что облигации на рынке обязательно будут продаваться по найденной цене. Так происходит потому, что различные вкладчики по-разному могут оценивать риск приобретения облигации, и, следовательно, использовать несколько отличные ставки дисконтирования. Кроме того, на цену будут также влиять силы спроса и предложения. Если спрос превышает предложение, то это создаст потенциал к повышению цены, если предложение больше спроса, то к понижению.

B. Определение доходности облигаций.

1.В.Определение доходности купонной облигации.

Текущая доходность. Текущая доходность определяется по формуле:

(5.22)

Где: r – текущая доходность; С – купон облигации; P – текущая цена облигации.

Пример 5.5. С - 20000 руб., Р - 80000 руб. Определить текущую доходность облигации. Она равна:

В знаменателе формулы (5.22) стоит текущая цена облигации. В следующий момент она может измениться, тогда изменится и значение текущей доходности.

Показателем текущей доходности удобно пользоваться, когда до погашения облигации остается немного времени, так как в этом случае ее цена вряд ли будет испытывать существенные колебания.

Доходность до погашения. Более объективным показателем доходности является доходность до погашения, так как при ее определении учитывается не только купон и цена бумаги, но и период времени, который остается до погашения, а также скидка или премия относительно номинала. Доходность облигации можно вычислить из формулы (5.9) Поскольку она содержит степени, то сразу определить доходность можно только с помощью специальной компьютерной программы. Можно воспользоваться также методом подстановки. Он состоит в том, что в формулу (5.9) последовательно подставляют различные значения доходности до погашения и определяют соответствующие им цены. Операцию повторяют до тех пор, пока значение рассчитанной цены не совпадет с заданной ценой. При совпадении цен мы получим искомую величину доходности до погашения. Поскольку цена и доходность облигации связаны обратной зависимостью, то в ходе подстановки, получив цену, которая выше данной, необходимо увеличить следующую цифру доходности, подставляемую в формулу. Если рассчитанная цена оказалась ниже заданной, необходимо уменьшить значение доходности.

(5.23)

Где: r - доходность до погашения; N - номинал облигации; Р - цена облигации; n - число лет до погашения;

С - купон.

Пример 5.6. N - 1000 руб., Р - 850 руб., n - 4 года, купон равен 15%. Определить доходность до погашения облигации.

Она равна:

Значение формулы (5.23) тем больше, чем больше цена облигации отличается от номинала и чем больше лет остается до погашения облигации. Если бумага продается со скидкой, то формула (5.23) дает заниженное значение доходности облигации, если с премией, то завышенное.

После того как инвестор определил значение доходности облигации с помощью формулы (5.23), он может воспользоваться формулой (5.24) для вычисления точной цифры доходности:

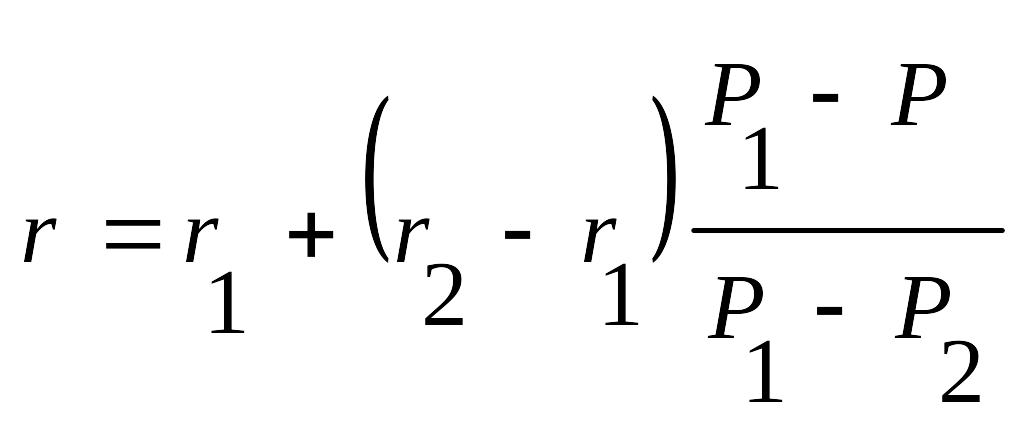(5.24)

Расчет по формуле (5.24) сводится к следующему. Вкладчик выбирает значение г₁ которое ниже полученного значения ориентировочной доходности, и рассчитывает для него соответствующую цену облигации P_i, воспользовавшись формулой (5.9). Далее берет значение r₂ которое выше значения ориентировочной доходности, и рассчитывает для него цену Р₂. Полученные значения подставляются в формулу (5.24).

Пример 5.7. Определить точную величину доходности облигации из приведенной выше задачи.

Мы рассчитали, что ориентировочная доходность облигации равна 20, 27%. Поэтому возьмем r₁, - 20% и r₂ - 21%. Тогда P₁ - 870,56 руб. и Р₂ - 847,57 руб.

Отсюда:

Таким образом, купив облигацию за 850 руб., инвестор обеспечит себе доходность до погашения равную 20, 89%.

Сделаем еще одно замечание. В формуле (5.24) купон выплачивался один раз в год. Соответственно в ответах получалось значение r равное простому проценту в расчете на год. Если по облигации купон выплачивается т раз в год, то можно пользоваться указанной формулой без всяких корректировок, т. е. не умножать количество лет на т и не делить купон на т. В этом случае мы также получим доходность бумаги как простой процент в расчете на год. В то же время, можно определить значение доходности, сделав указанную корректировку. Например, для облигации, по которой купон выплачивается два раза в год, формула ориентировочной доходности примет следующий вид:

(5.25)

Чтобы получить доходность за год, необходимо полученное значение умножить на 2.

2.B. Определение доходности бескупонной облигации. Вытекает из формулы (5.18):

(5.26)

Пример 5.8. N - 1000 руб., Р - 850 руб., n - 4 года. Определить доходность облигации.

Она равна:

Часть купонных облигаций имеет купоны, которые выплачиваются m раз в год, то формулу (5.26) необходимо скорректировать на величину m, т. е.:

(5.27)

Пример 5.9. N - 1000 руб., Р - 850 руб., n - 2 года, m - 2. Определить доходность облигации.

Она равна: