Порядок операций при обработке результатов серии измерений

При прямых измерениях:

1. Результаты каждого измерения записать в таблицу.

2. Вычислить среднее значение из n измерений

3. Найти погрешности отдельных измерений

.

4. Вычислить квадраты погрешностей отдельных измерений

(D x₁)², (D x₂)²,..., (D x_n)².

5. Оценить среднеквадратичную погрешность среднего значения

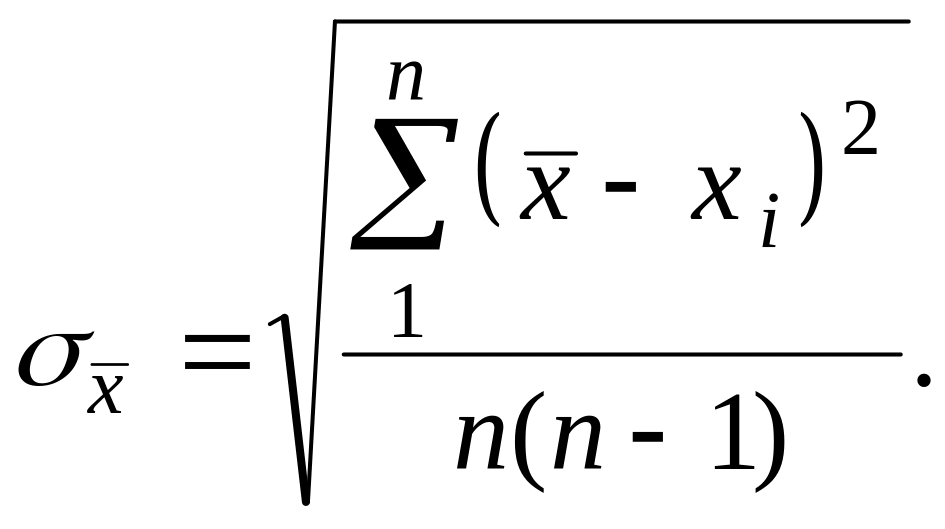
6. Определить коэффициент Стьюдента t_na (по таблице) для доверительной вероятности Р = 0,95 и числа произведенных измерений n.

7. Найти случайную погрешность результата измерений:

.

8. Если случайная погрешность результата измерений Dx окажется сравнимой^* с систематической (погрешностью прибора Dx_пр), то в качестве погрешности результата измерений следует взять величину

.

9. Окончательный результат записать в виде:

.

10. Оценить относительную погрешность результата измерений

.

При косвенных измерениях:

1. Для каждой непосредственно измеренной величины (X₁, X₂,..., X_m), входящей в расчетную формулу для определения X (X = f (X₁, X₂,..., X_m)), провести обработку в описанной выше последовательности, т.е. вычислить средние арифметические значения по формуле (1) и случайные погрешности D X₁, D X₂,..., DX_m по формуле (4) для доверительной вероятности Р = 0,95.

2. При необходимости учесть систематическую (приборную) погрешность каждой серии измерений

,

где индекс i относится к соответствующей измеренной величине, а DX_{пр i} – систематическая погрешность прибора, используемого для измерения Х_i.

3. Вычислить наиболее вероятное значение X:

4. Вычислить частные производные при средних значениях величин X₁, X_2,..., X_m.

5. Определить абсолютную погрешность косвенного измерения X по общей формуле:

.

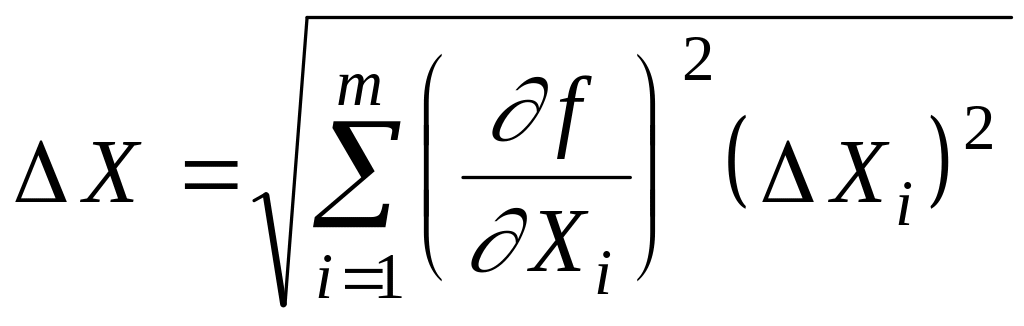Здесь и выше m – число независимых непосредственно измеренных величин.

6. Записать окончательный результат в виде

.

7. Определить относительную погрешность косвенного измерения X :

.

Правила представления результата измерения

Все результаты измерений, а также вычисленный по ним окончательный результат приводят вместе с погрешностью, которую выражают в тех же единицах, что и саму измеряемую величину, например: l = (1,572 ± 0,004) м.

Среднее значение <x> необходимо округлять так, чтобы оно оканчивалось цифрой того же разряда, что и Δх после её округления. Т.е. число и его погрешность всегда записывается так, чтобы их последние цифры принадлежали одному и тому же десятичному разряду. Значения погрешностей следует округлять, оставляя одну значащую цифру². Округлять предпочтительно в сторону большего значения.

Примеры:

1. Получено: U = 124,4 В; ΔU = 1,1 В.

Следует записать: U = (124,0 ± 1,0) В.

2. Получено: V = 2,678•10³ см/с; ΔV = 1,2 см/с.

Следует записать: V = (2,678 ± 0,001)•10³ cм/с.

В промежуточных выкладках при расчете погрешностей нужно удерживать три-четыре значащие цифры.

При представлении окончательных результатов физических измерений часто применяют запись числовых значений в виде десятичной дроби, умноженной на необходимую степень числа десять.

Примеры:

1. При обработке группы результатов измерений получены: 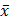= 965,332 и Δх = 8,35.

Результат округления записывают в виде: х = 965 ± 8.

2. При обработке группы результатов измерений получены: = 0,003893 и Δх = 0,000282.

Результат округления записывают в виде: х = (38,9 ± 2,8)•10⁴.

3. Числа 3106; 0,0285; 0,120 записывают так:

3,106•10³; 2,85•10^-2; 1,2•10^-1.

Графическое представление результатов измерений

В большинстве лабораторных работ требуется представить результаты в виде различного рода графиков. Их правильное построение требует соблюдения несложных правил.

1. Масштабы и начала отсчета по координатным осям выбираются так, чтобы график изображения зависимости занимал большую часть поля чертежа. При этом на пересечении осей не обязательно должны находиться нулевые значения величин.