55

Усов В.В.

Рішення задач з механіки та молекулярної фізики Методичні настанови для самостійної роботи студентів

 

Одесса 2012 

ББК

У

Рецензенти:

А.А. Брюханов,

д-р т. н., професор кафедри фізики

Південноукраїнського національного

педагогічного університету

імені К.Д. Ушинського.

Друкується за рішенням Вченої ради Південноукраїнського національного

педагогічного університету імені К.Д. Ушинського

протокол № _____.от _________ 2012 г.,

В.В. Усов

У РІШЕННЯ ЗАДАЧ З МЕХАНІКИ ТА МОЛЕКУЛЯРНОЇ ФІЗИКИ Методичні настанови. – Одесса: , 2012. – с.

ISBN

Викладені основні формули з механіки та молекулярної фізики в межах курсу загальної фізики педагогічних університетів. Запропоновані методичні настанови щодо рішення задач та приведені повні рішення деяких задач з усіх розділів механіки та молекулярної фізики, запропоновані задачі для самостійного рішення.

ББК

ISBN

Південноукраїнський національний педагогічний університет імені К.Д. Ушинського

 В.В. Усов

ОСНОВНІ ФОРМУЛИ

Механіка

1. • Кінематичне рівняння руху матеріальної точки уздовж осі х:

х = f (t)

де f(t) - деяка функція часу.

1. • Середня швидкість:

2. 

1. • Середня шляхова швидкість:

,

де S - шлях, пройдений точкою за інтервал t.

1. • Миттєва швидкість:

2. .

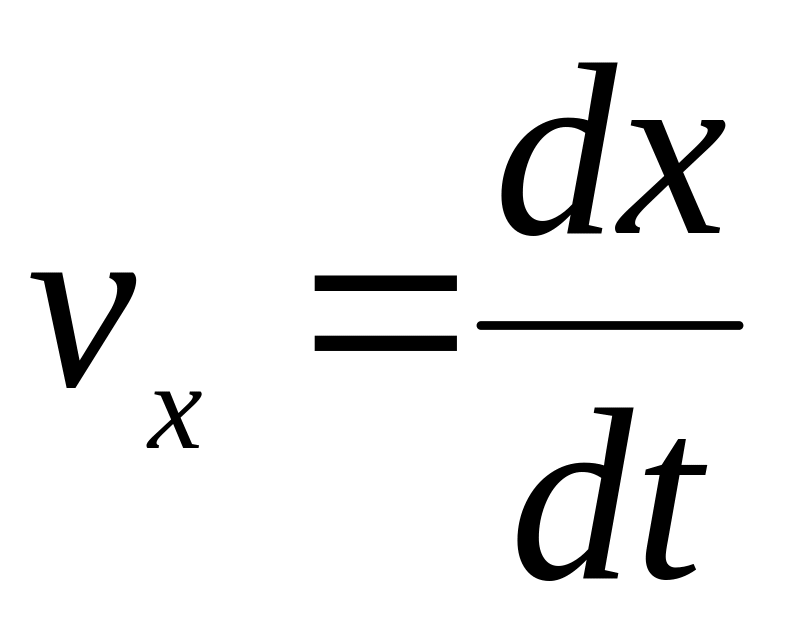1. • Середнє прискорення:

2. 

• Миттєве прискорення:

.

1. • Кінематичне рівняння руху матеріальної точки по колу:

 = f(t) ; r = const.

• Кутова швидкість (модуль):

.

• Кутове прискорення (модуль):

.

• Зв'язок між лінійними і кутовими величинами, що характеризують рух по колу:

ν = ωR ; a_τ = εR ; a_n = ω²R ,

де v - лінійна швидкість; a_τ і a_n – тангенціальне і нормальне прискорення; ω - кутова швидкість; ε - кутове прискорення; R - радіус кола.

1. • Повне прискорення:

або .

1. • Кут між повним прискоренням а і нормальним a_n :

α = arccos(a_n/a).

1. • Кінематичне рівняння гармонійних коливань матеріальної точки:

х = Acos(t+)

де х - зсув, А - амплітуда коливань,  - кругова або циклічна частота  - початкова фаза.

1. • Швидкість матеріальної точки, що здійснює гармонійні коливання:

v = -A sin(t+).

1. • Прискорення матеріальної точки, що здійснює гармонійні коливання:

а = -A2cos(t+).

1. • Період коливань математичного маятника:

,

де l - довжина маятника, g - прискорення вільного падіння.

1. • Період коливань фізичного маятника:

,

де J - момент інерції відносно осі коливань, m - маса тіла, а - відстань від осі обертання до центру мас тіла.

1. • Імпульс тіла:

,

де m - маса тіла, v - швидкість тіла.

1. • Другий закон Ньютона:

,

де F - сила, діюча на тіло, m - маса тіла.

1. • Сили, що розглядаються в механіці:

а) сила пружності F = -kx

де k - коефіцієнт пружності, х - абсолютна деформація;

б) сила тяжіння F = mg

в) сила тертя F = fN

де f - коефіцієнт тертя, N - сила нормального тиску.

1. • Закон збереження імпульсу:

2. 

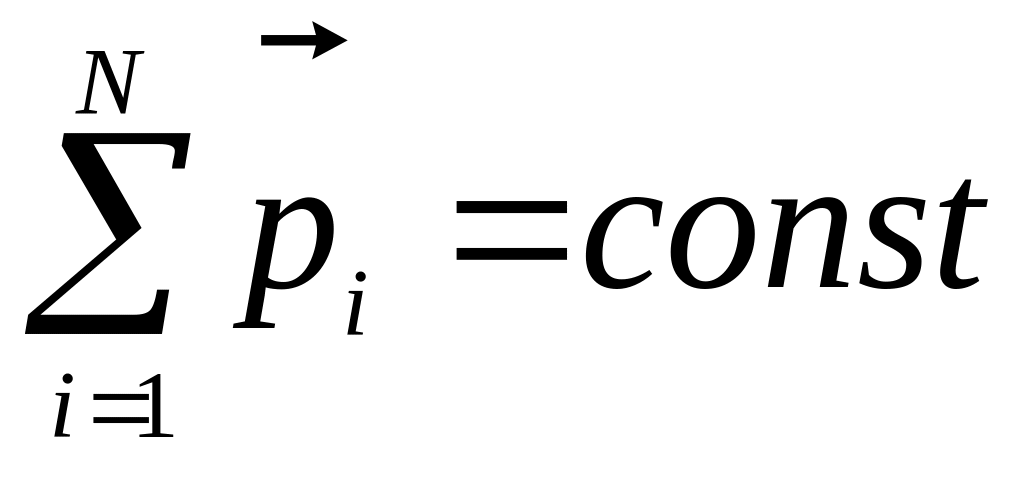
1. • Кінетична енергія тіла, що рухається поступально:

або .

1. • Потенційна енергія:

а) пружно деформованої пружини:

,

б) тіла, що знаходиться в однорідному полі сили тяжіння:

П = mgh

де h - висота тіла над рівнем, прийнятим за нульовий (формула справедлива за умови h << R, де R - радіус Землі).

1. • Закон збереження механічної енергії:

E = T+П = const.

1. • Основне рівняння обертального руху тіла навколо нерухомої осі:

M_z = J_zε ,

де M_z – проекція на вісь обертання z результуючого моменту зовнішніх сил, діючих на тіло, ε - кутове прискорення, J_z - момент інерції тіла відносно осі обертання.

1. • Моменти інерції деяких однорідних тіл маси m відносно осі, що проходить через центр мас:

а) стрижня довжини l відносно осі, перпендикулярної до стрижня:

;

б) обруча (тонкостінного циліндра) відносно осі, перпендикулярної до площини обруча (співпадаючій з віссю циліндра):

J = mR²

де R - радіус обруча (циліндра);

в) диска радіусом R відносно осі, перпендикулярної до площини диска (співпадаючій з віссю диска):

.

1. • Момент інерції тіла відносно довільної осі (теорема Штейнера):

J = J₀ + ma²

де J₀ - момент інерції тіла відносно осі, що проходить через центр мас паралельно заданої осі; m - маса тіла; а - відстань між осями.

1. • Момент імпульсу тіла, що обертається навкруги нерухомої осі z:

L_z = J_z

де  - кутова швидкість тіла навкруги осі обертання z .

1. • Закон збереження моменту імпульсу системи тіл, що обертаються навкруги нерухомої осі:

2. .

1. • Кінетична енергія тіла, що обертається навкруги нерухомої осі:

.