2. Проектировочный расчет

По известной нагрузке и заданному материалу (известной величине [σ]) подбираются размеры поперечного сечения, обеспечивающие прочность стержня:

.

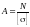3. Расчет на грузоподъемность

По известным размерам поперечного сечения и характеристикам прочности материала определяют допускаемое значение внутреннего силового фактора (в случае растяжения и сжатия – продольной силы):

N ≤ A[σ],

после чего находится наибольшее допускаемое значение нагрузки.

Пример 1. Расчет статически определимого стержня на растяжение, сжатие

Для заданного круглого ступенчатого стержня с жестко закрепленным концом, используя условие прочности, определить диаметры участков стержня и вычислить полное перемещение свободного конца стержня.

Д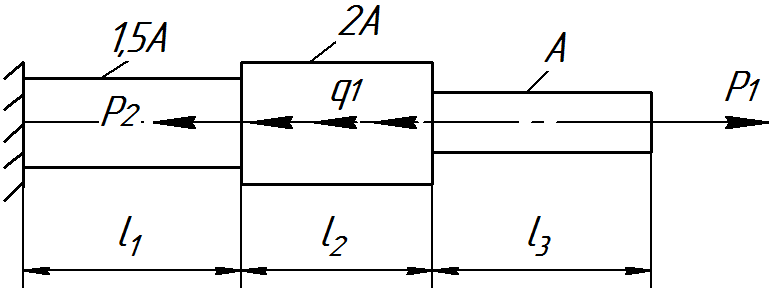 ано:

P₁ = 15 кН; Р₂ = 18 кН; q = 14 кН/м;

l₁ = 0,2 м; l₂ = 0,5 м; l₃ = 0.3 м;

Е = 2·10⁵ МПа; [] = 160 МПа

Решение.

1. Построить эпюру продольных сил.

а) 1-е сечение

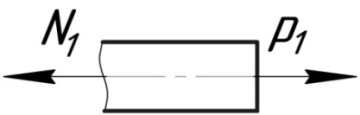
(растяжение);

б) 2-е сечение

,

,

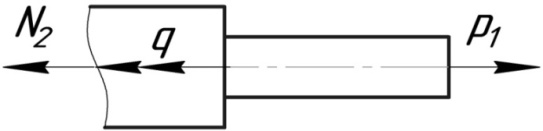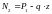при z=0 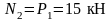(растяжение),

при z=0.5 (растяжение);

в) 3-е сечение

,

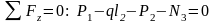(сжатие).

2. Определить опасное сечение, для него записать условие прочности и найти площадь поперечного сечения A:

,

где N – внутреннее усилие на участке;

A – площадь поперечного сечения.

, ,

, .

Условие прочности при растяжении-сжатии:

, , .

3. Определить диаметр каждой ступени стержня:

,

при A₁ = A , принимаем d₁=11 мм;

при A₂ = 2A , принимаем d₂=16 мм;

при A₃ = 1.5 A 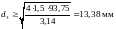, принимаем d₃=14 мм.

4. Построить эпюру нормальных напряжений:

,

, ,

, .

5. Вычислить полное перемещение свободного конца стержня:

,

где  – нормальное напряжение;

l₀ – первоначальная длина участка;

_{Е – модуль упругости материала стержня.}

Так как перемещение в заделке отсутствует, то перемещение начинаем рассчитывать от заделки:

.

Перемещение последующих участков определяется как собственное перемещение с учетом деформации предыдущего участка:

,

.

Эпюры стержня при растяжении-сжатии изображены на рис. 2.6.

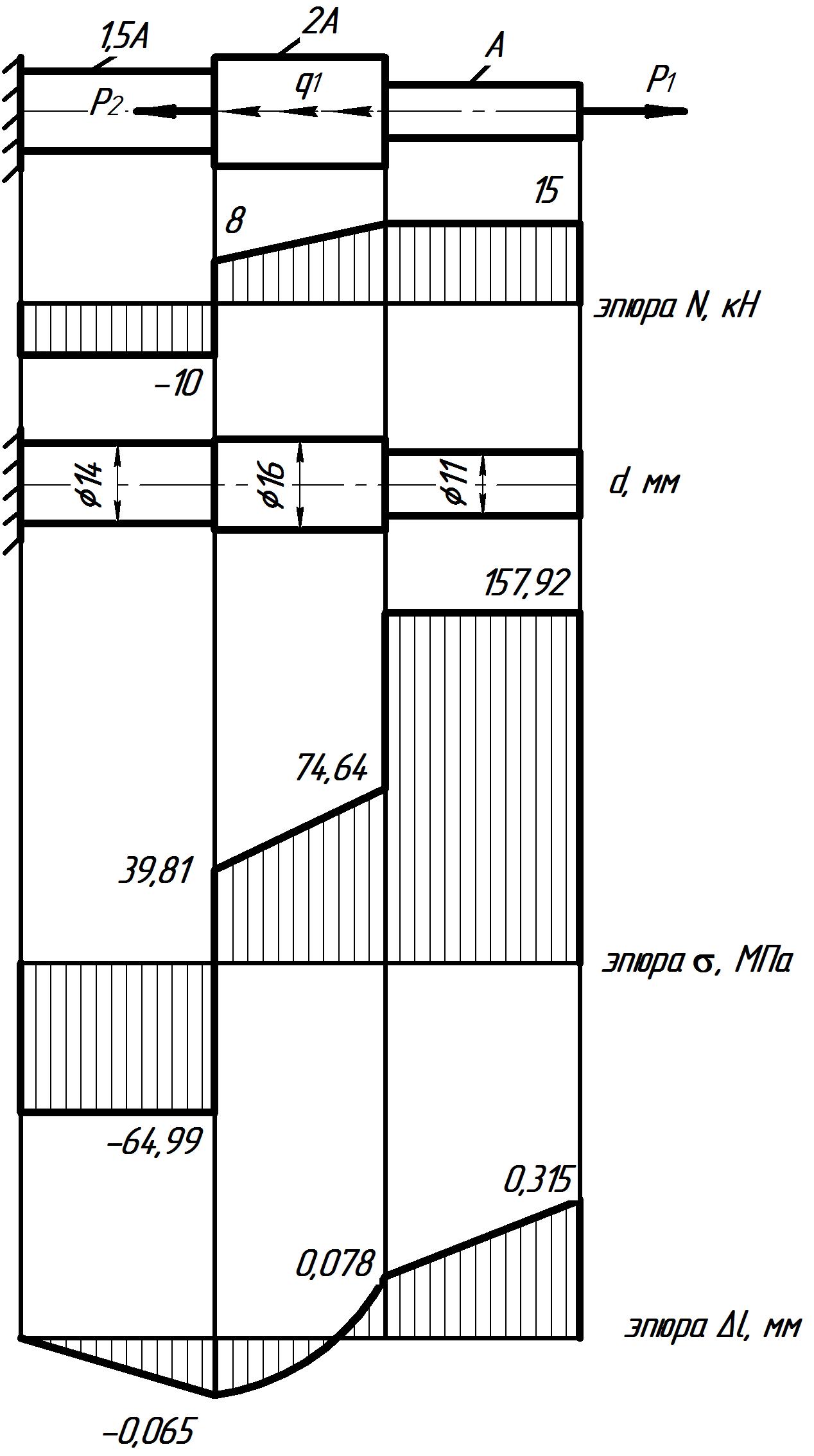
Рисунок 2.6.

Пример 2. Расчет на прочность статически определимых стержневых систем

П одобрать из условия прочности поперечные сечения стальных стержней кронштейна, нагруженного силой Р=200 кН, и определить горизонтальное, вертикальное и полное перемещение узла С (рис.2.7).

Стержень АС двутаврового поперечного сечения, стержень ВС круглого поперечного сечения. Допускаемое напряжение для материала стержней []=160 МПа, модуль упругости Е=210⁵ МПа.

Решение.

1. Составить уравнения равновесия и определим усилия в стержнях.

Для этого мысленно вырежем узел С. В сечениях стержней приложим неизвестные пока усилия в направлении, вызывающем растяжение стержней (рис.2.8).

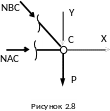
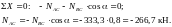
Отрицательное значение усилия N_АС указывает на то, что стержень АС испытывает сжатие.

2. Подобрать из условия прочности размеры стержней.

а) Для стержня ВС , причем 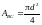. Тогда .

Принимаем в соответствие с таблицей нормальных размеров d=52 мм.

Площадь стержня ВС

б) Для стержня АС

.

В соответствии с сортаментом на двутавровые балки по ГОСТу 8239-89 принимаем двутавр № 14 с A=17,4 см².

3. Найти изменение длины каждого стержня.

а)Удлинение стержня ВС

.

б) Укорочение стержня АС

4. Определить перемещение узловой точки С.

П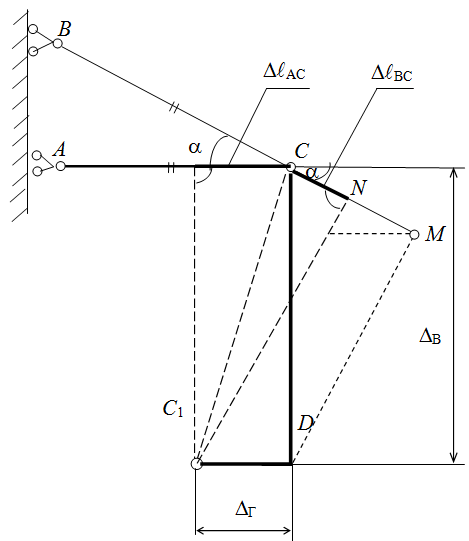

Рисунок 2.9. Перемещение узловой точки

лан перемещения представлен на рис.2.9. Для определения перемещения узла С положим, что стержни в узле С не соединены между собой. Тогда стержень ВС удлинится на величину _ВС, и стержень АС укоротится на величину _АС. Новое положение узла С (точка С₁) определится как точка пересечения перпендикуляров к стержням ВС и АС, проведенных из конца стержней ВС+_ВС и АС_АС (вместо дуг радиусов ВС+_ВС и АС_АС). Из схемы видно, что горизонтальное перемещение точки С равно _Г=|_АС|=1,23 мм. Для нахождения второй координаты точки С₁  _В проведем из точки D перпендикуляр на продолжение стержня ВС. Тогда удлинение _ВС можно представить как разность отрезков или , откуда

.

Полное перемещение узла С определяется как геометрическая сумма .
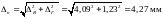