Механические характеристики материалов

Механические характеристики материалов, определяемые при растяжении, можно разделить на три группы.

1. Характеристики упругих свойств: модуль упругости первого рода (модуль Юнга) – Е; коэффициент Пуассона – .

2. Характеристики прочности: σ_пц – предел пропорциональности; σ_у – предел упругости; σ_т – предел текучести; σ_в – предел прочности.

3. Характеристики пластичности:

Относительное остаточное удлинение после разрыва – отношение приращения расчетной длины образца (ℓ_К – ℓ₀) после разрушения к начальной расчетной длине ℓ₀, выраженное в процентах

.

Относительное сужение после разрыва ψ – отношение разности A₀ и минимальной A_к площади поперечного сечения после разрушения к начальной площади поперечного сечения образца A₀, выраженное в процентах

.

Чем пластичнее материал, тем больше относительное удлинение и относительное сужение после разрыва. Материалы условно подразделяют на пластичные (δ_к > 5 %) и хрупкие (δ_к < 5 %).

2.6. Расчеты на прочность при растяжении

Основной задачей расчета конструкции на растяжение является обеспечение ее прочности в условиях эксплуатации.

Метод допускаемых напряжений является основным при расчете машиностроительных конструкций. В его основе лежит условие прочности – оценка прочности элемента конструкции, сводящаяся к сравнению расчетных напряжений с допускаемыми

σ_max ≤ [σ],

которое для случая растяжения (сжатия) приобретает вид:

,

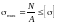где σ_max – наибольшее по величине напряжение, возникающее в опасных точках наиболее нагруженного сечения;

[σ] – допускаемое напряжение – наибольшее напряжение, которое можно допустить в элементе конструкции при условии его безопасной, долговечной и надежной работы.

Для каждого материала допускаемое напряжение находится по формуле:

,

где σ_пред – предельное напряжение (состояние), при котором конструкция перестает удовлетворять эксплуатационным требованиям, за которое принимают либо предел текучести при статическом нагружении для пластичных материалов, либо предел прочности для хрупких;

[n] – нормативный коэффициент запаса прочности; для пластичных материалов коэффициент запаса принимается обычно равным [n] = 1.4…1.6, для хрупких [n] = 2.5…3.5.

Запас прочности – отношение предельно допустимой теоретической нагрузки к той нагрузке, при которой возможна безопасная работа конструкции с учетом случайных перегрузок, непредвиденных дефектов и недостоверности исходных данных для теоретических расчетов.

В зависимости от той предельной характеристики, с которой сравнивают расчетное напряжение σ, различают [n_т] – нормативный коэффициент запаса прочности по отношению к пределу текучести σ_т и [n_в] – нормативный коэффициент запаса прочности по отношению к пределу прочности σ_в.

Основные виды расчета на прочность

Существует три основных вида расчетов.

1. Проверочный расчет

По заданной нагрузке и известным размерам сечения находится наибольшее напряжение, которое сравнивается с характеристикой прочности материала (допускаемым напряжением): σ_max ≤ [σ].

Для хрупкого материала условие прочности выглядит следующим образом:

;

,

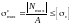где σ_р и σ_с – наибольшие расчетные растягивающие и сжимающие напряжения;

[σ_р] и [σ_с] – допускаемые напряжения при растяжении и сжатии.

Как вариант, находится фактический запас прочности:

,

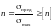который сравнивается с нормативным коэффициентом запаса [n].