2.2. Напряжения при растяжении (сжатии)

При растяжении (сжатии) в поперечных сечениях стержня возникают только нормальные напряжения. Для однородного стержня постоянного сечения при действии продольной силы N нормальные напряжения будут постоянными как по сечению, так и по всей длине. На основании гипотезы Бернулли (плоских сечений) и принципа Сен-Венана (о равномерном распределении напряжений по сечению) внутренние усилия:

Откуда .

2.3 Деформации при растяжении (сжатии)

При растяжении стержня происходит увеличение его длины и уменьшение поперечных размеров (рис. 2.4).

Деформация абсолютная (абсолютное удлинение) – Δℓ = ℓ₁ – ℓ.

Деформация относительная (продольная деформация) – ε = Δℓ / ℓ.

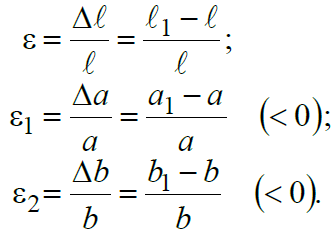
Рисунок 2.4. Изменение размеров стержня при его растяжении

Коэффициент поперечной деформации (коэффициент Пуассона) – абсолютная величина отношения поперечной относительной деформации к продольной (упругая постоянная материала):

 .

У всех существующих материалов значения коэффициента Пуассона находятся в пределах от 0 до 0,5. Конструкционные стали имеют μ = 0,25 ÷ 0,3. Значение коэффициента Пуассона, близкое к 0,5, свидетельствует о несжимаемости материала, т. е. независимости его объема от действующих нагрузок.

2.4. Связь напряжений и деформаций

В пределах малых удлинений для подавляющего большинства материалов справедлив закон Гука, который устанавливает прямую пропорциональность между напряжениями и деформациями:

,

где Е – модуль упругости первого рода, модуль Юнга, физическая константа материала. Модуль упругости характеризует сопротивление материала деформированию растяжением (сжатием) в упругой области.

Для сталей Е = 2·10⁵ МПа.



Закон Гука – нормальное напряжение σ прямо пропорционально относительной линейной деформации ε.

Подставив σ = N/A и ε = Δℓ/ℓ, получим иную форму записи закона Гука:

,

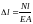где произведение E∙A – жесткость сечения при растяжении, характеризует способность материала стержня сопротивляться деформации растяжения (сжатия).

2.5. Механические характеристики конструкционных материалов

Основные прочностные и деформационные характеристики материалов, используемых в элементах конструкций, определяют экспериментально. Наиболее распространенным является испытание на растяжение статической нагрузкой, позволяющей определить большинство механических характеристик материала. Стандартами предусмотрены образцы плоские и цилиндрические (рис. 2.5). Цилиндрические образцы могут быть нормальные (с расчетной длиной l_расч=10d) и укороченные (с l_расч =5d). Для плоских образцов при вычислении расчетной длины образца используется диаметр круга, равновеликого поперечному сечению рабочей части образца.

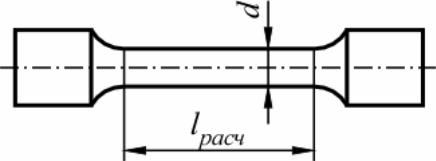
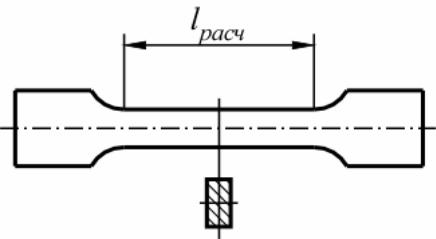
Рисунок 2.5. Образцы для испытаний

В процессе растяжения, реализуемого на специальных испытательных машинах, автоматически записывается диаграмма испытания в координатах сила – удлинение. Для малоуглеродистой стали эта диаграмма выглядит следующим образом:

Основные участки диаграммы:

OB – участок упругости.После нагружения в пределах этого участка образец возвращается в исходное состояние. Такая деформация, полностью исчезающая после разгрузки, называется упругой.

BC – участок общей текучести (площадка текучести). После разгрузки образец не возвращается в исходное состояние, приобретая остаточную, или пластическую, деформацию.

CD – участок упрочнения. Пластическая деформация изменяет внутреннюю структуру материала, в результате чего образец снова проявляет сопротивление деформированию, и растягивающая сила повышается.

DK – участок местной текучести. Точка D диаграммы соответствует появлению на образце локального сужения – шейки. Дальнейшая деформация локализуется в этой области, и за счет уменьшения площади поперечного сечения необходимая для растяжения сила снижается. Точка K соответствует разделению образца на части. Разрыв происходит в самом тонком месте шейки.

Чтобы исключить влияние геометрических размеров образца, рабочая диаграмма перестраивается в условную (в координатах напряжение – деформация):

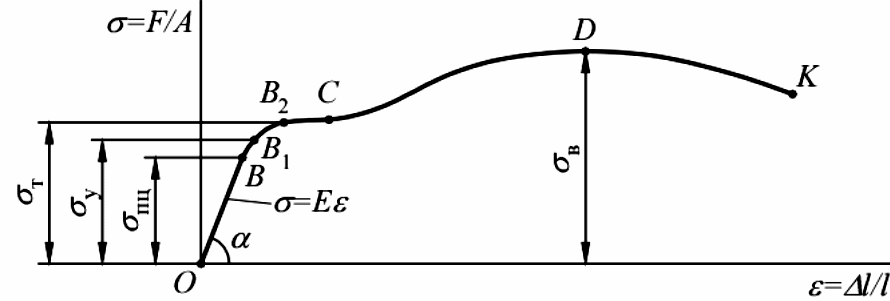
Полученная диаграмма называется условной потому, что при вычислении напряжения и деформации сила и удлинение относятся не к действительным, а к начальным значениям соответственно площади поперечного сечения и длины образца.

На условной диаграмме выделяют следующие характерные точки:

σ_пц – предел пропорциональности – максимальное напряжение, до которого справедлив закон Гука (т.е. наблюдается прямая пропорциональная зависимость между напряжением и деформацией);

σ_у – предел упругости – максимальное напряжение, до которого в материале не возникает пластических деформаций;

σ_т – предел текучести – напряжение, при котором наблюдается рост деформации при постоянном напряжении;

σ_в – предел прочности (или временное сопротивление разрыву) – максимальное напряжение, которое может выдержать образец без разрушения.

В момент разрыва истинное напряжение, отнесенное к действительной площади сечения, существенно выше предела прочности.