1.5 Понятие о напряжениях

Напряжение – величина, характеризующая интенсивность внутренних усилий в точке.

Е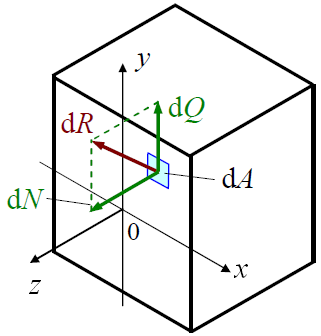 сли в поперечном сечении A некоторого тела выделить элементарную площадку А (рис.1.4), в пределах которой действует равнодействующая внутренних сила R, то за полное напряжение в точке сечения (при А стремящейся к нулю) может быть принято отношение:

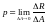
Н

Рисунок 1.4. Разложение элементарного внутреннего усилия на составляющие

апряжение нормальное σ (сигма) – перпендикулярное к сечению, характеризует интенсивность сил отрыва или сжатия частиц элементов конструкции.

.

Напряжение касательное  (тау) – действующее в плоскости сечения, характеризует интенсивность сил, сдвигающих эти части в плоскости сечения.

.

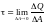Напряжение полное .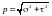

Единица измерения давления и механического напряжения паскаль (обозначение Па). Паскаль – давление, вызываемое силой 1 Н, равномерно распределенной по поверхности площадью 1 м².

1



Па = 1 Н/м²; 1 МПа = 0,102 кгс/мм²; 1 МПа = 10,2 кгс/см²;

1 МПа = 1 Н/мм²; 1 кгс/мм² = 9,81 МПа.

1.6. Виды деформаций

Реальные тела не являются абсолютно твердыми и под действием приложенных сил могут изменять свое положение в пространстве, свои размеры и форму.

П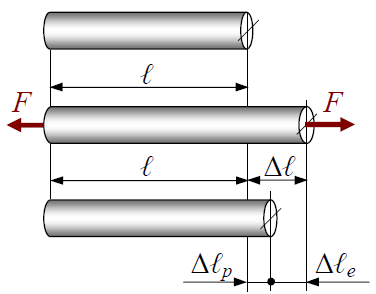 еремещение – изменение положения в пространстве точки или поперечного сечения.

Деформация – изменение формы и размеров тела под действием приложенных сил.

Деформация упругая Δℓe – исчезающая после снятия нагрузки.

Деформация пластическая Δℓp – остающаяся после снятия нагрузки.

Д

Рисунок 1.5. Составляющие деформации растяжения

еформация абсолютная (полная) – Δℓ = Δℓe + Δℓp.

Д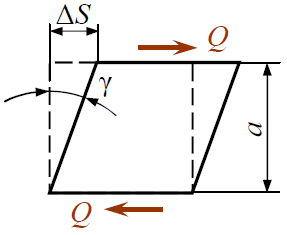 еформация относительная

ε = Δℓ / ℓ.

ΔS – абсолютный сдвиг.

γ – относительный сдвиг, угловая деформация, угол сдвига

.

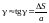Рисунок 1.6. Деформация сдвига

2. Растяжение и сжатие

2.1. Внутренние усилия

Растяжение (сжатие) – вид деформации, при котором в поперечных сечениях стержня возникает только один внутренний силовой фактор – продольная сила N.

Д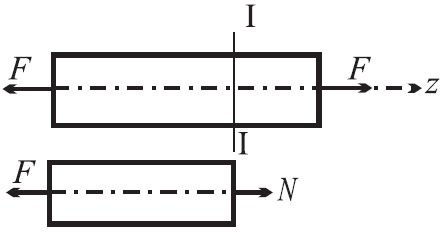 ля нахождения нормальных сил применяется метод сечений – стержень мысленно рассекается плоскостью, перпендикулярной его оси, на две части. Взаимодействие частей стержня заменяется силой N, величина которой определяется из условия равновесия какой-либо из частей (рис. 2.1).

Σ

Рисунок 2.1

Fz=0: –F+N=0

N=F

П



родольная сила N считается положительной, если она вызывает растяжение (направлена от сечения), и отрицательной, если она вызывает сжатие (направлена к сечению) (рис. 2.2).

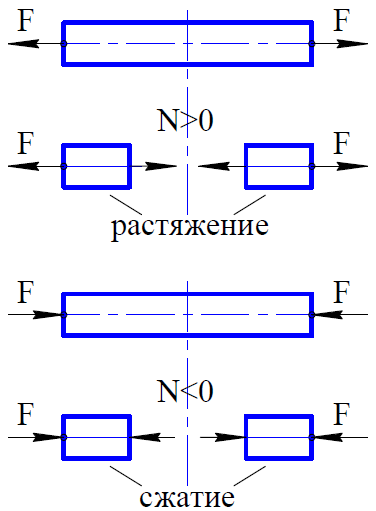
Рисунок 2.2.

В произвольном сечении продольная сила численно равняется алгебраической сумме проекций на ось стержня всех внешних сил, действующих по одну сторону от данного сечения:

.

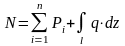Внешние силы, направленные от сечения входят в уравнение со знаком плюс, а направленные к сечению – со знаком минус, что соответствует указанному выше правилу знаков для продольной силы.

Интенсивность сил тяжести в пределах каждого участка ступенчатого стержня будет величиной постоянной и равной:

,

где  – вес единицы объема материала, A – площадь поперечного сечения.

При растяжении – сжатии интенсивность распределенной нагрузки и продольная сила связаны между собой следующей дифференциальной зависимостью:

.

Стержень – брус, работающий на растяжение или сжатие. Для определения опасного участка строят эпюры внутренних усилий и напряжений.

Эпюра – график, изображающий закон изменения внутренних усилий или напряжений по длине бруса, а также напряжений по поперечному сечению бруса.

При построении эпюры следует руководствоваться некоторыми правилами, вытекающими как из метода сечений, так и из дифференциальной зависимости между q и N:

1 Если на участке стержня отсутствует распределенная нагрузка, то продольная сила постоянна.

2



Если на участке имеется равномерно распределенная нагрузка, то продольная сила изменяется по линейному закону.

3 В сечении, где приложена внешняя сосредоточенная сила, эпюра продольных сил имеет скачок на величину этой силы.

4 В концевых сечениях стержня продольные силы равны приложенным в этих сечениях внешним сосредоточенным силам.

Пример 1. Построение эпюры продольных сил.

Стержень разбивается на силовые участки, границами которых служат сечения, где приложены сосредоточенные нагрузки, либо начинается или заканчивается действие распределенных нагрузок. В данном примере стержень имеет три участка. Для нахождения нормальной силы на каждом из участков поочередно мысленно проводится сечение, рассекающее стержень на две части. Записывая условия равновесия для показанных на рисунке отсеченных частей стержня, получаем выражения для нормальной силы на каждом из выделенных участков:

I. 0 ≤ z ≤ 2l	II. 0 ≤ z ≤ l	III. 0 ≤ z ≤ 2l
qz + N = 0; N = −qz; N(0)=0; N(2l)=-2ql;	q2l + N = 0; N = −2ql;	2ql − 3ql − 2qz+ N = 0; N = ql + 2qz; N(0)= ql; N(2l)=5ql.

На основе этих уравнений строится эпюра N(z) (рис. 2.3).

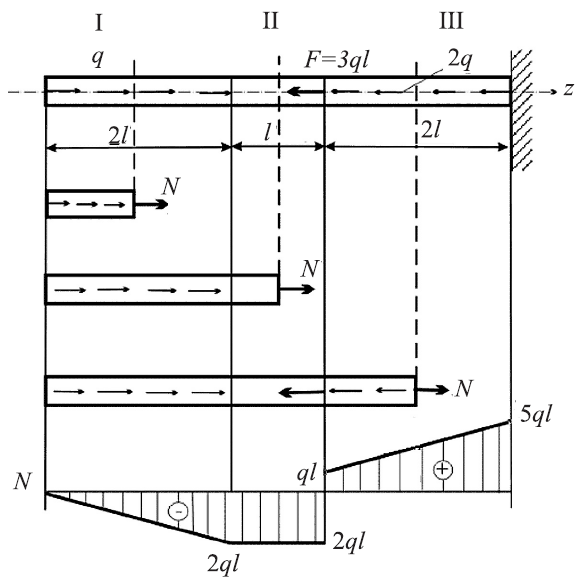
Рисунок 2.3. Эпюра продольных сил