Силовая схематизация (модель нагружения)

В нагруженном теле, находящемся в равновесии, внешние нагрузки стремятся вызвать деформацию тела, а внутренние усилия стремятся сохранить тело как единое целое.

Внешние нагрузки – силы взаимодействия между рассматриваемым элементом конструкции и другими телами, связанными с ним.

Классификация внешних нагрузок производится по трем признакам: способу приложения, продолжительности действия, характеру изменения.

По способу приложения: сосредоточенные, распределенные.

Сосредоточенными называют силы, если они приложены к площади, размеры которой малы по сравнению с площадью поверхности всего тела. например, давление обода колеса на рельс. Размерность Н, кгс (ньютон, килограмм силы).

Распределенными по площади (поверхностными) называют силы, приложенные к площадкам контакта, например, давление жидкости или газа на стенки сосуда, снеговая нагрузка на кровлю здания.

Давление выражается в единицах силы, отнесенных к единице площади, Н/м2, кгс/см2. Производная единица Паскаль: 1 Па = 1 Н/м2.

Распределенные по длине равномерно или по заданному закону (треугольному, параболическому). Размерность Н/м, кгс/м.

Объемные силы непрерывно распределены по объему, занимаемому элементом, например, сила тяжести, сила инерции. Характеризуются интенсивностью, то есть отношением единицы силы к единице объема, Н/м , гс/см.

По продолжительности действия: постоянные и временные.

Постоянные действуют в течение всего времени существования конструкции.

Временные действуют на протяжении отдельных периодов эксплуатации объекта, например, давление газа в баллоне.

По характеру изменения в процессе приложения:

Статические– постоянные (нагрузка от собственного веса), или медленно и незначительно изменяющие величину, направление и точку приложения так, что силами инерции вследствие ускорения можно пренебречь

Динамические – характеризующиеся быстрым изменением во времени величины, направления или точки приложения и вызывающие в конструкции или отдельных ее элементах большие ускорения, которыми пренебречь нельзя. Величина этой нагрузки значительно изменяется за малые промежутки времени, например, ударная.

Повторно-переменные (циклические) – периодически изменяющие величину и/или знак по некоторому закону.

1.4. Метод сечений для определения внутренних усилий

Для прочностных и деформационных расчетов необходимо определить внутренние усилия.

Внутренние усилия – силы взаимодействия между частицами тела (кристаллами, молекулами, атомами), возникающие внутри элемента конструкции, как противодействие внешним нагрузкам.

Д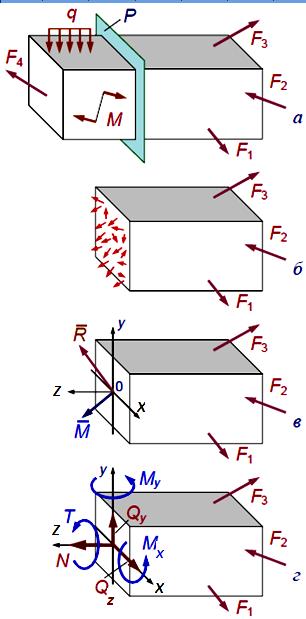 ля выявления внутренних усилий используют метод сечений.

1. Рассечь мысленно нагруженное тело плоскостью Р на две части (рис. 1.3, а).

2. Отбросить одну из частей (рис. 1.3, б). Реальное тело представляет собой конгломерат различно ориентированных зерен, от граней которых в разных направлениях действуют элементарные внутренние усилия.

3. Заменить действие отброшенной части внутренними усилиями. Систему внутренних сил можно привести к главному векторуR и главному моменту М. За точку приведения обычно принимают центр тяжести сечения 0 (рис. 1.3, в) Выбрав систему координат х, у, z (z – продольная ось по нормали к поперечному сечению, x и y – в плоскости этого сечения) и начало системы в центре тяжести, обозначим проекцию главного вектора R на координатные оси через N, Q_x, Q_y, а проекции главного момента М – М_х, М_у, М_z.

Рисунок 1.3. Определение внутренних усилий методом сечений

Эти три силы и три момента называют внутренними силовыми факторами в сечении:

N – продольная сила;

Q_x, Q_y – поперечные силы;

M_z – крутящий момент;

M_x, M_y – изгибающие моменты.

4. Уравнения равновесия позволяют определить внутренние усилия. Всего их шесть:

три силы – проекции главного вектора R:

X=0; Q_x=...;

Y=0; Q_y=...;

Z=0; N=...;

три момента – проекции главного момента М:

 M_x=0;

M_y=0;

M_z=0.

Правило определения внутренних силовых факторов: внутренние силы N, Qy, Qх численно равны алгебраической сумме проекций всех внешних сил (в том числе и реакций), приложенных к телу по одну сторону от рассматриваемого сечения. Аналогично: внутренние моменты Мх, My, Mz численно равны алгебраической сумме моментов от внешних сил, действующих по одну сторону от рассматриваемого сечения.

Краткая последовательность основных этапов метода сечения:

Р



– рассечь тело на две части плоскостью;

О – отбросить одну из частей тела;

З – заменить действие отброшенной части внутренними усилиями;

У – уравнения равновесия составить.