1. Как найти вершины многоугольника.

2. Как организовать рациональный перебор решений.

В ХТС связи между входными и выходными параметрами описываются в общем случае нелинейными зависимостями. Однако в определенных пределах изменения входных параметров возможна линеаризация этих зависимостей, а также ограничений, накладываемых на входные и управляющие переменные. Величины, влияющие на ход технологического процесса по физическому смыслу неотрицательны. Поэтому для оптимизации ХТС можно использовать методы линейного программирования.

Наиболее часто методы линейного программирования используются для решения технико-экономических задач. Суть их состоит в нахождении набора параметров технологического процесса, который удовлетворяет ограничениям на ресурсы, плановым заданиям и максимизируют при этом доход предпрития.

VII. Динамическое программирование.

Этот метод применяется при оптимизации многостадийных процессов. Если на последней стадии не будет оптимальным процесс, то не будет оптимальным весь многостадийный процесс в целом. Поэтому оптимальный режим всего процесса определяется постадийно, начиная с последней стадии, т.е. процесс разбивается на стадии во времени и пространстве.

Преимущество метода – резкое сокращение числа опытов при оптимизации.

Трудности возникают в методе подбора для каждой стадии.

П араметры управления

u_N u_i u_i-1 u₁

N

i

i - 1

1

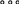
x_N+1 x_N x_i+1 x_i x_i-1 x₂ x₁

z_N z_i z_i-1 z

математическая модель каждой стадии

Даны допустимые области переменных состояний

Известен вектор начального состояния x_N+1=α и критерий оптимальности для каждой стадии процесса. Тогда задача оптимизации многостадийного процесса можно сформулировать как задачу нахождения оптимальной стратегии ( ), для которой

VIII. Симплексный метод оптимизации

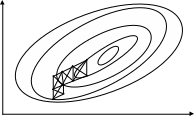
X₁

70

80 60

90

50

X₂

Аналитические методы оптимизации

Метод множителей Лагранжа.

Используется, когда на переменные наложены ограничения типа равенства.

Так, если требуется найти экстремум функции F(x₁, x₂,…, x_n) при наличии ограничений f_i(x₁, x₂,…, x_n)=0, причем i-1,2,…,m m<n, то для решения этой задачи вводится вспомогательная функция

В этом случае экстремальные точки функции F(x₁, x₂,…, x_n) определяются решением системы уравнений, получаемой приравниванием к нулю производных от функции по всем независимым переменным х_к(к=1,…,n) и по всем множителям Лагранжа . Получаемая система уравнений содержит n+m уравнений

Пример

Определить размеры открытого прямоугольного бака емкостью 1000м³ при условии min поверхности дна и стенок. Объем бака V=lbh.

h

b

l

Решение: целевая функция – минимизировать площадь, т.е. минимизировать функцию F(l,b,h)=2hb+bl+2hl

Ограничения: f_i(b,h,l)=0, т.е. f_i(b,h,l)=lbh-V=0

Вспомогательная функция имеет вид:

Берем частные производные по l, b, h, λ.

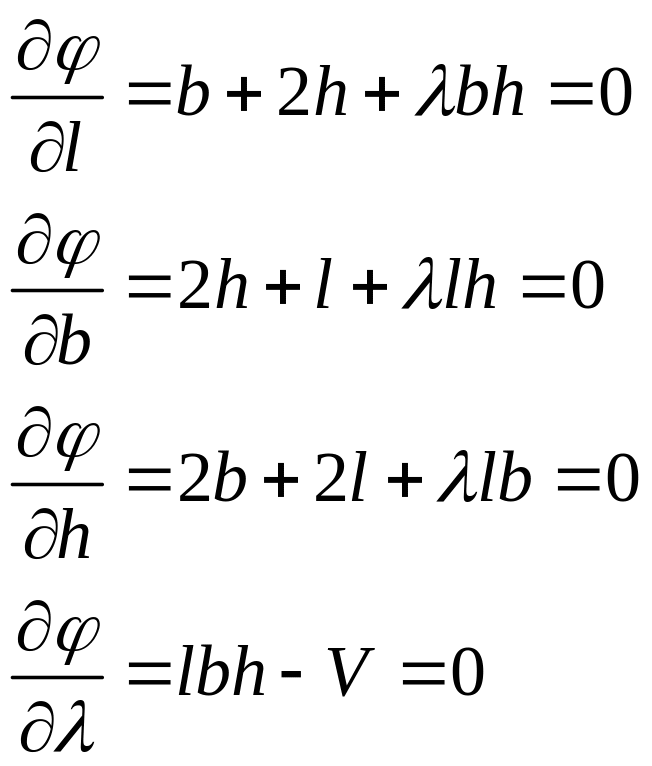
Из первого уравнения получаем ;

Из второго уравнения получаем: b=l;

Из третьего уравнения находим: .

Из первого уравнения следует: b=2h.

Следовательно , значит l=12,6м b=12,6м, h=6,3м.

Оптимизация ХТС и биотехнологических систем с помощью искусственно создаваемых колебательных режимов.

Одна из возможностей интенсификации процессов химической технологии - использование периодических изменений управляющих воздействий и переменных, характеризующих состояние процесса.

При таком нестационарном периодическом режиме в целом ряде случаев средняя производительность аппарата за цикл оказывается больше, чем в оптимальном режиме с неизменными параметрами. Следует отметить, что качество продукта при этом повышается.

В качестве примера можно взять процесс грануляции (сушки) в псевдоожиженном слое. Производительность процесса зависит от количества тепла, вносимого в слой.

V – скорость газового потока (теплоносителя)

F – площадь аппарата

T_вх – температура на входе

T_сл – температура в слое

C – теплоемкость

Обычно V и F величины постоянные в условиях промышленной эксплуатации аппарата.

T_вх – держат на уровне максимально возможной.

Единственный параметр варьирования остается T_сл и значит, что температура в слое определяет производительность аппарата и, следовательно, для увеличения производительности аппарата необходимо поддерживать температуру в слое (T_сл) на уровне минимально возможной.

Но на T_сл накладываются ограничения, связанные с качеством продукта, а именно с гранулометрической характеристикой.

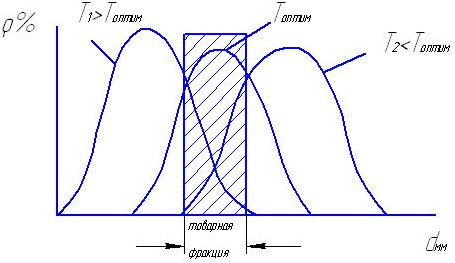
Значит Т₁<Т_оптим<Т₂ для обеспечения качества продукта.

Для увеличения производительности использован колебательный температурный режим.

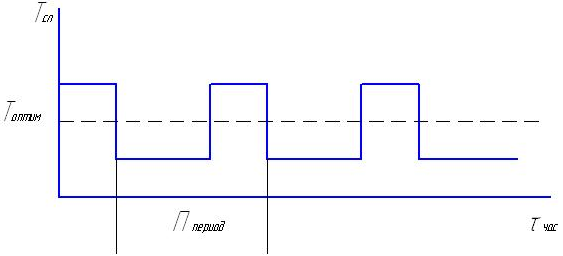
при Т₂ – 3/4П

при Т₁ – 1/4П

Производительность увеличивается по сравнению с Т_оптим. Но это возможно при большом времени релаксации процессов грануляции, т.е. когда гранулообразование не успевает следить за колебаниями температуры в слое.