Оптимизация химико-технологических процессов.

Целью моделирования является оптимизация любого ХТП и биотехнологического процесса. Оптимизация – целенаправленный поиск значений факторов (параметров), при котором достигается экстремум критерия оптимальности (с учетом ограничений, накладываемых на факторы и функции отклика).

Критерий оптимальности – величина, характеризующая уровень оптимизации, обычно это одна из выходных функций. Обычно функций отклика много, но не разработаны методы оптимизации по нескольким критериям. Поэтому одно из требований оптимизации – единственность критерия оптимизации. Оптимизация осуществляется в условиях ограничений на факторы и функции отклика, существуют ограничения типа равенства и неравенства. h_i=a_i, где h_i – контролируемый, но нерегулируемый фактор

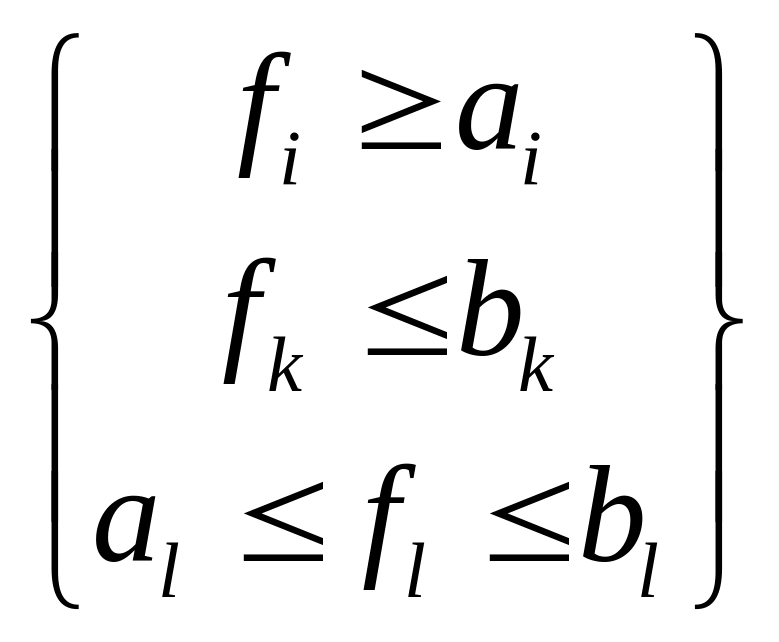- определяет пределы, в которых допустимо изменение параметров процесса f (оптимально для создания и реализации статистического решения)

Оптимизирующие факторы – факторы, которые в процессе оптимизации отсекаются к управляющим и применяются для оптимизации. Число оптимизируемых факторов зависит от стадии оптимизации. Оптимизация при проектировании – число факторов растет, т.к. оптимизация не в действительности, а при моделировании.

Оптимальное управление – оптимизация после пуска производства.

Целевая функция – это тоже самое, что и критерий оптимальности и рассматривается как функция входных факторов , тогда оптимум – это экстремум целевой функции.

Методы оптимизации можно разделить на 3 основные группы:

1. Аналитические методы – когда можно продифференцировать целевую функцию и искать экстремум из условия равенства 0 производных.

2. Численные методы – необходимо иметь алгоритм расчета целевой функции, т.Е. Можно по нему рассчитать значение критерия оптимальности при заданных значениях факторов.

3. Планирование эксперимента – когда функция не вычисляема – экспериментальная оптимизация.

Аналитические методы оптимизации.

Аналитические методы являются классическими методами поиска экстремума и применяются когда функция задана аналитически и число неизвестных параметров невелико. Осложняется применение аналитических методов наличием ограничений и поэтому применение их ограничено. Аналитический поиск целевой непрерывной функции сводится к приравниванию производных к 0: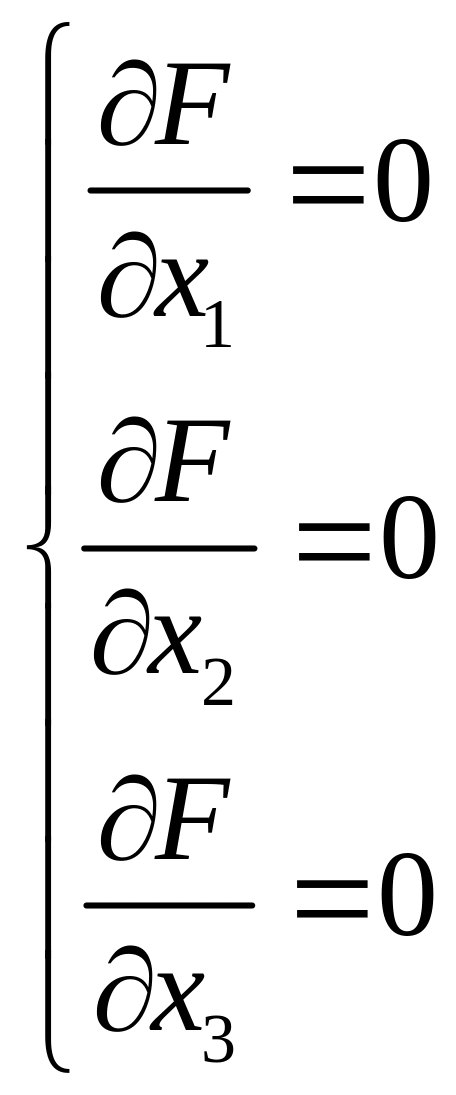

Классический метод анализа функции одной переменной F(x₁) позволяет найти координаты точек экстремума из условия F'(x₁)=0. Вид экстремума выясняется из известного правила для второй производной

Если F''(x₁)>0 – min+

Если F''(x₁)<0 -max-

Если число переменных больше 1, то поиск усложняется.

Для функции двух переменных 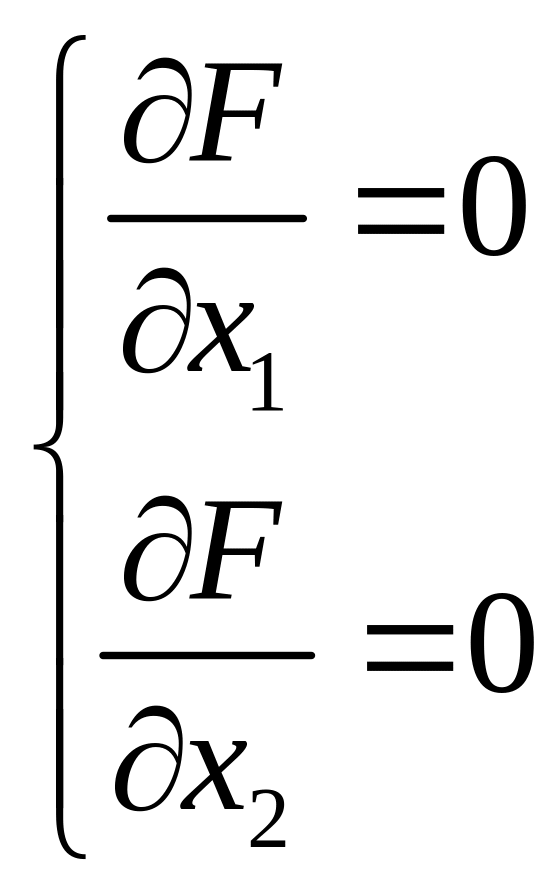и для проверки экстремума исследуется выражение

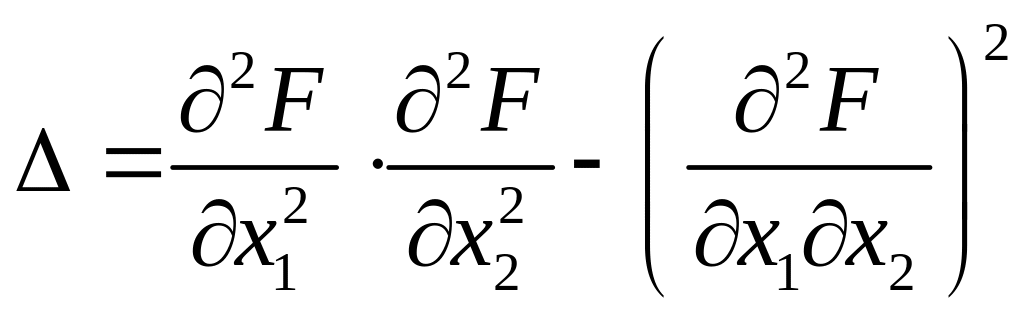
Если , то есть экстремум, при <0 имеется Max

при >0 имеется min

Если , то нет экстремума.

К аналитическим моделям относятся:

1. метод Лагранжа (он используется при наложении ограничений типа равенства).

2. метод линейного программирования.

3. метод динамического программирования.

Численные методы.

Численные методы применяются в следующих случаях:

1. когда в точке экстремума отсутствуют производные. Например, изменение целевой функции имеет дискретный характер. При непрерывной функции это возможно, если экстремум находится на краю области допустимых значений.

2. если функция в точке экстремума дифференцируема, но в общем виде продифференцировать ее трудно. Например, она задана не формулой, а алгоритмом.

3. если полученное решение громоздко.

В общем виде численные методы сводятся к тому, что вычисляется ряд значений F при различных значениях аргумента. Сравнение этих значений показывает в каком направлении надо двигаться в пространстве факторов, чтобы приблизиться к оптимуму.

I. Метод перебора

F(x)

x

Этот метод применяется если число возможных вариантов конечно. Достаточно рассчитать целевую функцию и выбрать их них наилучшее (Min,max). Например, для случая ферментации имеется ряд аппаратов (дискретный ряд) и число ярусов мешалки (точно дискретно) и перебором определяется наилучший. Этот метод легко осуществить на ЭВМ. Метод прост и эффективен. Это может быть ряд теплообменников, сушильных агрегатов и т.д.