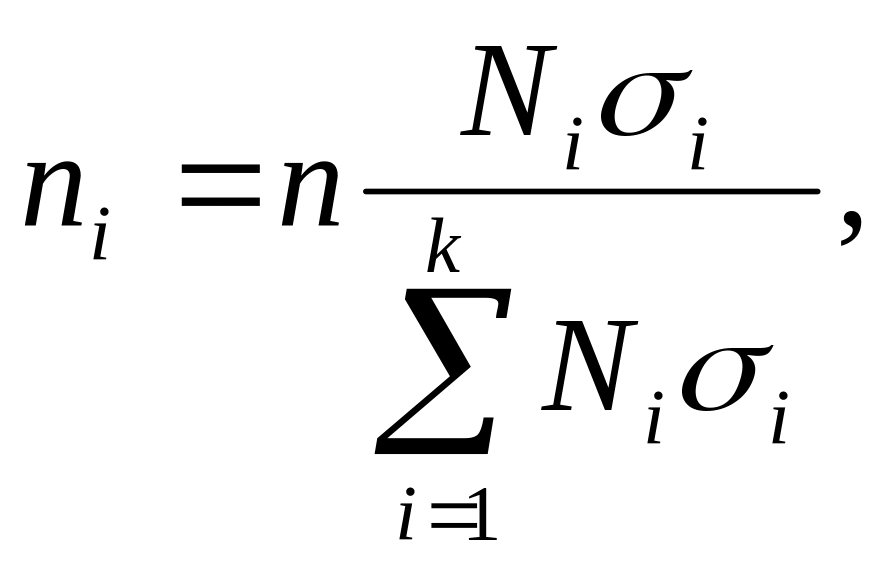- •Статистика
- •Предисловие
- •Раздел 1. Аналитическая статистика
- •Тема 1. Предмет и метод статистики
- •1.1. Предмет статистики и ее теоретическая основа.
- •Статистическая наука имеет три уровня:
- •1.2. Основные аспекты организации статистики
- •1.2.1. История статистики
- •1.2.2. Организация статистических служб в России
- •1.2.3. Международные статистические организации.
- •Тема 2. Статистическое наблюдение
- •2.1. Этапы проведения и программно-методологические вопросы статистического наблюдения.
- •2.2. Формы, виды и способы организации статистического наблюдения.
- •2.3. Точность наблюдения
- •Тема 3. Сводка и группировка статистических данных
- •3.1. Задачи и виды статистической сводки
- •3.2. Метод группировок в статистике.
- •3.3. Принцип построения группировок
- •3.4. Ряды распределения в статистике.
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Тема 4. Способы наглядного представления статистических данных
- •4.1. Табличное представление данных
- •4.1.2. Виды статистических таблиц
- •Пример решения задачи
- •4.2. Графическое изображение данных
- •Ленточная диаграмма
- •Распределение населения одного регион по полу и возрасту
- •Радиальные диаграммы
- •Сезонные колебания производства мяса в одном из регионов России в 2001 г.
- •Задачи для самостоятельного решения
- •Тема 5. Статистические показатели
- •5.1. Понятие статистических показателей.
- •5.2. Абсолютные и относительные величины в статистике.
- •5.3.Относительные величины
- •Обавить взаимосвязь!!!!!!!!!
- •5.4. Средние величины в статистике.
- •Примеры решения задач
- •Примеры решения задач
- •5.5. Структурные средние (мода, медиана).
- •Примеры решения задач
- •Примеры решения задач
- •Тема 6. Показатели вариации в статистике
- •Вариация признака в совокупности и значение ее изучения
- •3. Правило сложения дисперсий
- •Примеры решения задач
- •3. Дисперсия альтернативного признака
- •Примеры решения задач
- •5) Коэффициенты вариации Va.
- •Задачи для самостоятельного решения
- •Тема 7. Индексы в статистике
- •7.1. Понятие и классификацию индексов в статистике
- •7.2. Индексы структурных сдвигов
- •7.3. Оценка динамики цен на товары и измерение уровня инфляции
- •Пример решения задачи
- •Тема 8. Выборочное наблюдение
- •8.1. Понятие выборочного наблюдения
- •8.2. Способы формирования выборочной совокупности:
- •Отбор единиц в выборочную совокупность
- •8.3. Методы оценки результатов выборочного наблюдения
- •8.4. Оценка результатов выборочного наблюдения и распространение его данных на генеральную совокупность
- •8.5. Практика применения выборочного наблюдения в социально-экономических исследованиях
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Тема 9. Статистическое изучение связи между явлениями
- •9.1. Методы изучения связи между явлениями.
- •Корреляционно-регрессионный анализ
- •Примеры решения задач
- •Тема 10. Ряды динамики
- •10.1. Виды и методы анализа рядов динамики.
- •Правила построения динамических рядов
- •10.2. Показатели рядов динамики:
- •Пример решения задачи
- •10.3. Анализ взаимосвязанных рядов динамики.
- •10.4. Методы выравнивания рядов динамики.
- •10.5. Анализ сезонных колебаний
- •Классификация методов измерения сезонной волны
- •Примеры решения задач
- •Метод укрупнения интервалов.
- •Динамика поквартальной продажи безалкогольных напитков в одной из республик за 3 года
- •Задачи для самостоятельного решения
Отбор единиц в выборочную совокупность
Специальные этапы проведения выборочного наблюдения:
определение необходимого объема выборки и способа отбора;
проведение отбора;
обобщение данных наблюдения и расчет выборочных характеристик;
расчет ошибок выборки.
Численность выборки при собственно случайном и механическом отборе
Вид выборочного наблюдения
|
Повторный отбор
|
Бесповторный отбор |
а) при определении среднего размера признака
|
п = t22 / ∆2x
|
п = t2x2N / ( ∆x2 + t2)
|
б) при определении доли признака
|
п = t2 w(I – w / ∆2w |
п = t2 w(I – w)N / ∆2 +t2 w(l- w) |
Распределение между районами
|
||
пропорциональное |
непропорциональное |
оптимальное |
|
|
|
где ni - число наблюдений из i-й типической группы; n - общий объем выборки; Ni - объем i –й типической группы в генеральной совокупности |
где k — количество выделенных районов, число выделенных типических групп
|
где σi - среднее квадратическое отклонение изучаемого признака в i-й группе.
|
8.3. Методы оценки результатов выборочного наблюдения
Ошибки, свойственные выборочному наблюдению, называются ошибками репрезентативности или представительства
Систематические ошибки возникают в результате нарушения принципа случайности отбора единиц совокупности для наблюдения. Например, для обследования успеваемости в университете ошибочно отбирают наиболее подготовленных студентов с положительными отметками.
Случайные ошибки возникают ввиду того, что выборочная совокупность недостаточно точно воспроизводит всю совокупность из-за несплошного характера наблюдения.
Средняя величина ошибки для выборочной совокупности, отобранной в случайном порядке:
![]()
где μ — средняя ошибка выборки; σ — среднее квадратическое отклонение; n — численность выборочной совокупности.
Средняя ошибка (μ)
выборочных средней (х) и доли (w) для разных видов выборки
Вид выборки |
Отбор |
|
|
повторный |
бесповторный |
Количественный признак |
||
Собственно-случайная |
μ х = √ 2/n |
μ х = √ (2 (l-n/N) /n) |
|
|
|
Альтернативный признак |
||
Собственно-случайная |
μw =√ w(1-w)/n
|
μw = √ w(l-w)(l-n)/N)/n |
i 2 - средняя групповая выборочная дисперсия средней:
2 i - внутригрупповая; дисперсия данной (/-и) группы в выборочной совокупности;
w (1 - w) - средняя групповая выборочная дисперсия доли.
Формулы предельной ошибки позволяют решать задачи трех видов:
Определение пределов генеральных характеристик.
Определение доверительной вероятности.
Определение необходимого объема выборки.
Предельная ошибка выборки (∆) определяется по формуле
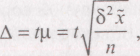
Величины генеральной средней и доли могут быть представлены интервальной оценкой в виде определения доверительного интервала по заданному уровню доверительной вероятности Р:
При значении t = 1 вероятность равна 0,683.
При значении t = 1,96 вероятность равна 0,950
При значении t = 2 вероятность равна 0,954.
При значении t = 3 вероятность равна 0,997.