Тема 6. Показатели вариации в статистике

Студент должен:

знать:

- понятие вариации и ее значение;

- абсолютные и относительные показатели вариации;

уметь:

- оценить степень вариации изучаемого признака путем расчета абсолютных и относительных показателей вариации.

Вариация признака в совокупности и значение ее изучения

Различие индивидуальных значений признака внутри изучаемой со­вокупности в статистике называется вариацией признака

Исследование вариации позволяет:

• определить уровень зависимости изучаемого яв­ления от прочих факторов, т.е. оценить степень ус­тойчивости явления к внешним воздействиям;

• определить уровень однородности изучаемого яв­ления;

• изучить явления, протекающие в обществе, характе­ризующиеся высоким уровнем их изменчивости.

	В иды вариаций:
альтернативная	систематическая	случайная
признак может принять только одно из двух, противоположных по своей сути, значений	изменение признака в определен­ном направлении, не обусловленное внутренними за­конами развития исследуемого явления	изменчивость признака не предсказуема.

Рисунок 6.1. Виды вариаций

Для того чтобы руководитель предприятия, менеджер, научный работник могли управлять вариацией и изучать ее, статистикой разработаны специальные методы исследования вариации — система показателей. С их помощью вариация измеряется, характеризуются ее свойства. К показателям вариации относятся: размах вариации, среднее линейное отклонение, дисперсия и среднее квадратичное отклонение, коэффициент вариации.

Исследование вариации позволяет:

• Определить уровень зависимости изучаемого явления от прочих факторов, т. е. оценить степень устойчивости явления к внешним воздействиям;

• Определить уровень однородности изучаемого явления;

• Изучить явления, протекающие в обществе, характеризующиеся высоким уровнем их изменчивости.

При статистическом анализе вариационных рядов используются различные показатели (меры) вариации в зависимости от поставленных перед исследователем задач. К ним относятся:

• размах вариации,

• среднее линейное отклонение,

• средний квадрат отклонений (дисперсия),

• среднее квадратическое отклонение и

• коэффициент вариации.

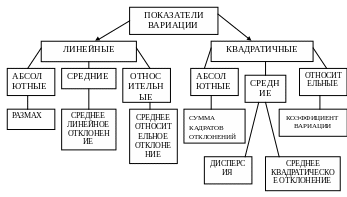
Рисунок 6.2. Показатели вариации.

Абсолютные показатели вариации:

• Размах вариации (R) является наиболее простым измерителем признака:

R = x_max - x_min

• Среднее линейное отклонение ( d ) учитывает разли­чия всех единиц исследуемой совокупности. Данная величина определяется как средняя арифметическая из абсолютных значений отклонений, взятых по модулю, от средней. Различают простое (невзвешенное и взвешенное среднее линейное отклонение:

• среднее линейное отклонение невзвешенное определяется по формуле:

d = Σ Iх_i - I / n

где х_i – величина совокупности, – средняя, n – количество признаков

• среднее линейное отклонение взвешенное определяется по формуле:

d = Σ (х_i - )f_i / Σ f_i

f - частота

Этот показатель дает более полное представление о степени колеблемости признака по сравнению с размахом вариации.

Недостаток вычисления среднего линейного отклонения заключается в том, что приходится иметь дело не только с положительными, но и с отрицательными величинами;

• Дисперсии (групповая, межгрупповая и общая) и среднее квадратическое отклонение.

Дисперсия представляет собой сумму квадратов отклонений значений показателя от средней. Различают невзешенную и взвешенную дисперсии.

Дисперсия невзвешенная определяется по формуле:

Дисперсия взвешенная определяется по формуле:

Относительные показатели вариации.

• Коэффициент осцилляции (V_R):

V_R = R/x 100%

где R — размах вариации;

х — средняя величина.

Обычно данный показатель имеет значение больше еди­ницы, поскольку размах вариации в основном больше сред­ней величины.

• Коэффициенты вариации:

• линейный коэффициент вариации (Va):

Va = d/x100%

или Va= d/Me100%

где d — среднее линейное отклонение; Me — медиана.

Данный коэффициент показывает, какую часть в разме­ре средней величины (или в объеме медианы) составляет размер среднего линейного отклонения.

• покажзатель относительной вариации - коэффициент вариации ( V₎ :

V =  /x 100%

Данный коэффициент определяет удельный вес среднего квадратического отклонения в значении средней величины и служит мерой однородности совокупности. Чем больший коэффициент вариации, тем менее однородная совокупность и тем менее типична средняя для данной совокупно­сти. По величине коэффициента вариации можно судить о степени вариации признака изучаемой совокупности. Чем больше его величина, тем больше разброс значений признака вокруг средней, и тем менее представительна средняя. Установлено, что совокупность количественно однородна, если коэффициент вариации не превышает 33%.

Характеристика видов дисперсии

вид	алгоритмы и формулы расчета
Общая дисперсия: характеризуе6т меру вариации признака по всей изучаемой совокупности, обусловленную всеми факторами, включая и фактор, положенный в основание группировки	Рассчитывается по одной из известных формул
Групповая дисперсия: выступает мерой вариации признака в соответствующей группе, обусловленной всеми прочими факторами, кроме фактора, положенного в основание группировки	Представляет собой средний квадрат отклонений индивидуальных значений признака группы от средней этой группы. Расчет осуществляется по формуле: 2 i = Σ (хi - )2fi / Σ fi
Внутригрупповая дисперсия: выступает мерой вариации признака по всей совокупности, обусловленной всеми прочими факторами, кроме положенного в основание группировки; так называемая остаточная дисперсия	Эта средняя рассчитывается из групповых дисперсий по формуле: δ2 = Σ ( i - )2fi / Σ fi
Межгрупповая дисперсия: оценивает меру вариации признака по всей совокупности, обусловленную фактором, положенным в основание группировки Межгрупповая дисперсия характе-ризует вариацию результативного признака за счет группировочного признака.	Средний квадрат отклонений групповых средних от общей средней рассчитывается по формуле:

М ежгрупповая дисперсия равна среднему квадрату отклонений групповых с редних х_ от общей средней x.