Примеры решения задач

Пример 2.

Применение средней гармонической рассмотрим на следующем примере. Допустим, что бригада токарей была занята обточкой одинаковых деталей в течении 8-часового рабочего дня. Первый токарь затратил на одну деталь 12 минут, второй – 15 минут, третий – 11, четвертый – 16 и пятый – 14 минут. Определим среднее время, необходимое на изготовление одной детали. На первый взгляд кажется, что задача легко решается по формуле средней арифметической простой:

.

Полученная средняя была бы правильно найдена, если бы каждый рабочий сделал только по одной детали. Но в течение дня отдельными рабочими было изготовлено различное число деталей. Для определения числа деталей, изготовленных каждым рабочим, воспользуемся следующим соотношением: среднее время, затраченное на одну деталь равно

, где T – все затраченное время, N – число деталей.

Число деталей, изготовленных каждым рабочим, определяется отношением всего времени работы к среднему времени, затраченному на одну деталь. Тогда среднее время, необходимое для изготовления одной детали, равно:

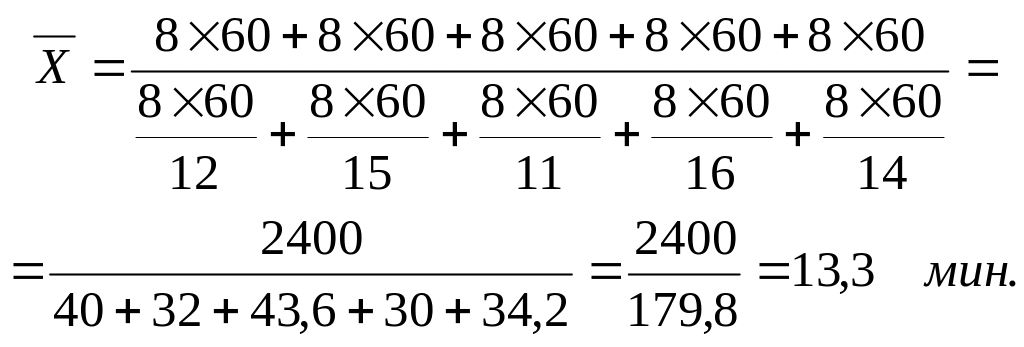
• средняя геометрическая (простая и взвешенная);

T_p = x П(Т^х_р), взвешенная

где Тр — средняя геометрическая взвешенная (средний темп прироста);

х. — количество периодов, при которых темпы роста ос­тавались неизменными.

• средняя степенная (квадратическая, кубическая);

квадратическая

5.5. Структурные средние (мода, медиана).

Модой (Мо) называют значение признака, наиболее часто встречающегося у единиц совокупности. В дискретном ряду модой будет вариант с наибольшей частотой.

Для дискретных рядов распределения модой будет значение варианты с наибольшей частотой. Например, распределение проданной обуви по размерам характеризуется следующими показателями:

Размер обуви	36	37	38	39	40	41	42	43	44	45 и выше
Число пар в % к итогу	–	1	6	8	22	30	20	11	1	1

В этом ряду распределения мода равна 41. Именно этот размер обуви пользуется наибольшим спросом покупателей.

Для интервальных рядов распределения с равными интервалами мода определяется по формуле:

M₀ = x_mo + h ((f_m-f_m-1) / [(f_m-f_m-1) +(f_m-f_m+1)]

где x₀ — нижняя граница модального интервала; h — величина модального интервала;

f_m — частота модального интервала;

f_{m_1} — частота интервала, предшествующего модальному;

f_m+1 — частота интервала, следующего за модальным.

Для определения моды сначала определяют модаль­ный интервал.

Модальный интервал представляет собой интервал, име­ющий наибольшую частоту.

Примеры решения задач

Пример 3.

Распределение предприятий по численности промышленно-производственного персонала характеризуется следующими данными

Группы предприятий по числу работающих чел.	Число предприятий	Группы предприятий по числу работающих чел.	Число предприятий
100–200	1	500–600	19
200–300	3	600–700	15
300–400	7	700–800	5
400–500	30
ИТОГО:			80

В этой таблице наибольшее число предприятий (30) имеет численность работающих от 400 до 500 чел. Следовательно, этот интервал является модальным интервалом ряда распределения. Введем следующие обозначения:

x_мо – 400; f_мо-1 – 7; f_мо – 30; i_мо– 100; f _мо+1 – 19.

Подставим эти значения в формулу моды и проведем вычисления. Получаем, что мода равна 467,8 ≈ 468 чел.

Медианой (М_е) – в статистике называется варианта расположенная в середине вариационного ряда. Если ряд распределения дискретный и имеет нечетное число, то медианой будет варианта, находящаяся в средине упорядоченного ряда (упорядоченный ряд – это расположение единиц совокупности в возрастающем или убывающем порядке). Медиана делит ряд на две равные части Например, стаж пяти рабочих составил 2, 4, 7, 8, 10 лет. В таком упорядоченном ряду медиана – 7 лет. По обе стороны от нее находится одинаковое число рабочих.

Если упорядоченный ряд состоит из четного числа членов, то медианой будет средняя арифметическая из двух вариант, расположенных в середине ряда. Пусть теперь будет не пять человек в бригаде, а шесть, имеющих стаж работы 2, 4, 6, 7, 8 и 10 лет. В этом ряду имеются две варианты, состоящие в центре ряда. Это варианты 6 и 7. Средняя арифметическая из этих значений и будет медианой ряда:

Медиана интервального вариационного ряда распределения определяется по формуле:

М_е = х₀ + h ((Σf_i/2 – S_Me-1)/N_Me)

где х_o— нижняя граница интервала; h — величина интервала; п — число членов ряда;

(m-l) — сумма накопленных членов ряда, предше­ствующих медианному;

N_Me—частота медианного интервала.