Примеры решения задач

Пример 1.

Пусть имеются следующие данные о заработной плате рабочих сдельщиков:

Заработная плата, тыс. руб.	Число рабочих	Х x 
Х1 = 110	f 1 = 2	220
Х2 = 130	f 2 = 6	780
Х3 = 160	f 3 = 16	2560
Х4 = 190	f 4 = 12	2280
Х5 = 220	f 5 = 14	3080
ИТОГО	50	8920

По данным дискретного ряда распределения видно, что одни и те же значения признака (варианты) повторяются по нескольку раз. Так варианта Х₁ встречается в совокупности 2 раза, а варианта Х₃ – 16 раз. Число одинаковых значений признака в рядах распределения называются частотой (или весом) и обозначается символом f.

Необходимо исчислить среднюю заработную плату одного рабочего ; среднюю заработанную плату одного рабочего , где А – заработная плата всех рабочих, N – число рабочих:

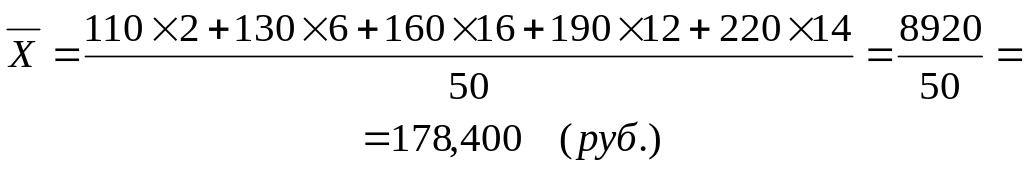
Фонд заработной платы по каждой группе рабочих равен произведению варианты на частоту, а сумма этих произведений дает общий фонд заработной платы всех рабочих.

Статистический материал в результате обработки может быть представлен не только в виде дискретных рядов распределения, но и в виде интервальных вариационных рядов с закрытыми или открытыми интервалами. Рассмотрим расчет средней арифметической для таких рядов.

Исчислим среднюю выработку продукции одним рабочим за смену. В данном ряду варианты осредняемого признака (продукции за смену) представлены не одним числом, а в виде интервала «от – до». Рабочие первой группы производят продукцию от 3 до 5 шт., рабочие второй группы от 5 до 7 шт., и т.д. Таким образом, каждая группа ряда распределения имеет нижнее и верхнее значение вариант, т.е. образовались закрытые интервалы.

Группы рабочих по количеству произведенной продукции за смену, штук	Число рабочих, 	Середина интервала, х	Хх 
3–5	10	4	40
5–7	30	6	180
7–9	40	8	320
9–11	15	10	150
11–13	2	12	60
ИТОГО	100		750

Исчисление средней по сгруппированным данным проводиться по формуле средней арифметической взвешенной.

.

Чтобы применить эту формулу, необходимо варианты признака выразить одним числом (дискретным). За такое дискретное число принимается средняя арифметическая простая из верхнего и нижнего значений интервала. Так, для первой группы дискретная величина Х будет равна:

и т.д.

Дальнейший расчет производится обычным методом определения средней арифметической взвешенной:

.

Итак, все рабочие произвели 750 штук изделий за смену, а каждый в среднем произвел по 7,5 штук.

Преобразуем рассмотренный выше ряд распределения в ряд с открытыми интервалами. Допустим, что имеются следующие данные о производстве продукции за смену.

Группы рабочих по количеству произведенной продукции за смену, штук	Число рабочих
до 5	10
5 – 7	30
7 – 9	40
9 – 11	15
свыше 11	5
ИТОГО:	100

В таких рядах условно величина интервала первой группы принимается равной величине интервала последующей, а величина интервала последней группы величине интервала предыдущей. Дальнейший расчет аналогичен изложенному выше.

Свойства средней арифметической значительно упрощает вычисления:

• если увеличить или уменьшить все варианты осредняемого признака на какое-либо одно и то же число, то объем средней величины соответственно увеличит­ся или уменьшится на это же число;

• если увеличить или уменьшить все варианты осредняемого признака в какое-либо число раз, то объем средней величины соответственно увеличится или уменьшится в это же количество раз;

• от увеличения или уменьшения веса каждого вариан­та признака в какое-либо число раз величина сред­ней не изменится. Применение данного свойства с практической точки зрения удобно, если необходимо проанализировать совокупность со значительным количеством элементов, а частота элементов выраже­на многозначными числами. Если частоты элементов равны между собой, то среднюю можно рассчитать как невзвешенную;

• как следствие предыдущего свойства можно сказать, что величина средней зависит не от абсолютных значений веса отдельных элементов, а от их доли в общей сумме весов, т.е. если не известны абсолютные выражения весов элементов, а известны пропорции между ними, то они могут использоваться для расчета средней;

• средняя арифметическая совокупности, состоящей из их постоянных величин, равна этой постоянной: х = х при х = const.

• средняя гармоническая (простая и взвешенная);

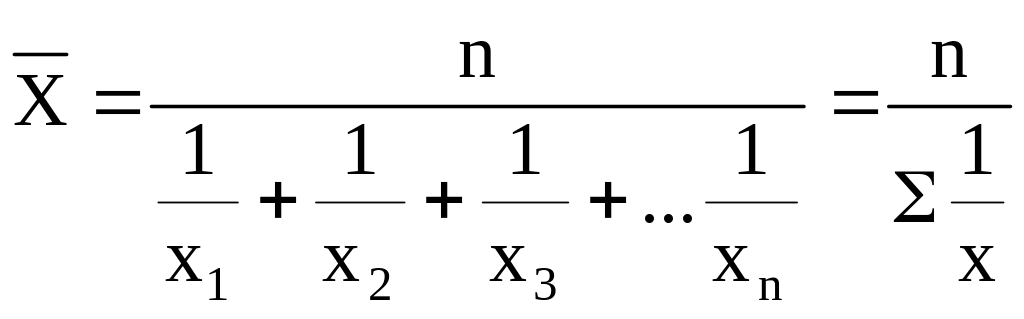простая

Взвешенная, где w — значение сводного, объемного, выступающего как признак-вес показателя:

.
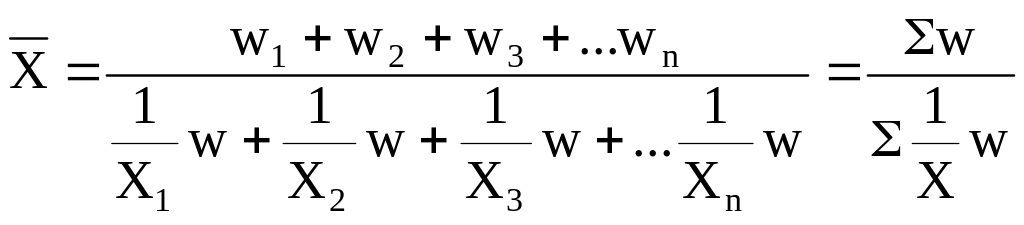