3.4. Ряды распределения в статистике.

Группировка позволяет получить такие результаты, по которым можно выявить состав типичных явлений, обнаружить закономерности и взаимосвязи. Результаты сводки могут быть представлены в виде статистических рядов распределения. Количественные ряды могут быть дискретными или интервальными.

Дискретный ряд распределения – это ряд, в котором варианты выражены целым числом. Примером может служить распределение рабочих по тарифным разрядам:

Примером может служить распределение рабочих по тарифным разрядам:

Тарифный разряд	1-й	2-й	3-й	4-й	5-й	6-й
Число рабочих, чел.	10	20	40	60	50	20

Интервальный ряд распределения – это ряд, в котором значения признака заданы в виде интервала.

Например, распределение рабочих по разрядам можно представить в виде интервального ряда:

Тарифный разряд	Число рабочих, чел.
1–2-й	30
3–4-й	100
5–6-й	70

Вариационные ряды состоят из двух элементов - вариантов и частот.

Варианта — это конкретное значение варьирующего призна­ка.

Частота — численность отдельных вариантов.

Сумма частот — это численность всей совокупности.

Частоты, выраженные в долях едини­цы или в процентах к итогу, называются частостями.

Для графического изображения дискретного вариационного ряда используют полигон распределения. Его изобража­ют в прямоугольной системе координат, где на оси абсцисс от­кладывают значение вариант х, а на оси ординат — частоты f. Полученные точки с координатами х. и f. соединяют прямыми ли­ниями. Для замыкания полигона конечные вершины соединяют с точками на оси абсцисс кото­рые отличаются на одно деление от х_mах и x_min.

Рисунок 3.4. Полигон распределения

Графическое изображение интервального вариационного ряда выполняют в виде гистограммы. Для рядов с равными интерва­лами строят гистограмму в осях «х -f». Для незакрыто­го первого интервала в качестве x_t берут среднее значение второго интервала, а для незакрытого последнего интервала – среднее значение предпоследнего х_т-1

Гистограмма для ряда с неравными интервалами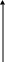

Рисунок 3.5. Гистограмма

В ряде случаев для изображения вариационных рядов использу­ется кумулянта. Для ее построения на оси абсцисс откла­дывают варианты х, а на оси ординат - накопленные частоты F. Изображение вариационного ряда в виде кумуляты удобно при сопоставлении вариационных рядов, а также в экономических ис­следованиях.

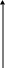F

х

Рисунок 3.6. Кумулята

Если при графическом изображении вариационного ряда в виде кумуляты оси поменять местами, то получим огиву.

Рисунок 3.7 Огива.

Графическое изображение рядов распределения позволяет на­глядно представить распределение данных статистического наблю­дения.

Группировка может быть научной лишь в том случае, если не только определены познавательные цели группировки, но и правильно выбрано основание группировки — группировочный признак. Если группировка — это распределение на однородные группы по какому-либо признаку или объ­единение отдельных единиц совокупности в группы, одно­родные по какому-либо признаку, то группировочный при­знак — это признак, по которому происходит объединение отдельных единиц совокупности в отдельные группы.

При выборе группировочного признака важным являет­ся не способ выражения признака, а его значение для изу­чаемого явления