Контрольні запитання.

1. Що таке сила поверхневого натягу і де вона спостерігається в природі?

2. Який фізичний зміст коефіцієнта поверхневого натягу?

3. Що ви зяєте про газову емболію і її лікування?

4. Де застосовується в медицині явище капілярності?

5. Задача.

Визначіть силу, що діє на барабанну перетинку пірнальника, який знаходиться на глибині 5м під водою, якщо площа барабанної перетинки становить 0,66∙ 10^-4м². (Застосуйте формули р = ρgh, F = pS ).

6. Задача.

З крапельниці накапали однакові маси води, спочатку холодної – при температурі 8⁰С, а потім гарячої – при температурі 80⁰С. Як і в скільки разів змінився коефіцієнт поверхневого натягу води, якщо в першому випадку утворилося 40, а в другому 48 крапель?

Лабораторна робота №4.

Тема: «Визначення коефіцієнта в’язкості рідин».

Мета роботи: Визначення коефіцієнта в’язкості рідин. Визначення в’язкості крові різними способами та її залежності від стану судин. Розв’язування задач.

Дотримання правил техніки безпеки, охорони праці в галузі, професійної безпеки в практичній діяльності.

Обладнання: капілярний віскозиметр, модель віскозиметра ВК – 4, слайди.

Теоретичні відомості.

1. Під час течії рідини між її сусідніми шарами виникають сили, які при­скорюють шар рідини, що рухається повільніше, й гальмують шар рідини, що рухається з більшою швидкістю. їх називають силами внутрішнього тертя. Влас­тивість рідини чинити протидію переміщенню її шарів відносно один одного називають в'язкістю рідини.

Сила внутрішнього тертя, що діє між двома шарами рідини площею S, які знаходяться на відстані Δr один від одного (мал. ЗО) і рухаються зі швидкостями визначається за формулою

д е η — коефіцієнт пропорційності, який

н ази­вають коефіцієнтом в'язкості, або

просто в'яз­кістю рідини. Вираз, узятий у

д ужки, — градієнт швидкості — являє Δr S

с обою приріст швидкості на одиницю

відстані між шарами рідини.

Таким чином, сила внутрішнього тертя

пря­мо пропорційна площі двох сусідніх

шарів рідини й градієнту швидкості між

ними. Це є закон Нью­тона для внутрішнього

тертя в рідинах. Він застосовний і для газів.

В'язкість переважної більшості рідин залежить від природи й температури рідини. З підвищенням температури коефіцієнт в'язкості рідин швидко змен­шується. В'язкість газів майже в 10⁵ разів менша, ніж рідин, і з підвищенням температури збільшується.

Виходячи з формули (2.6), установимо одиницю в'язкості в СІ:

Одиниця в'язкості в СІ не набула широкого вжитку. На практиці в'язкість рідини, як правило, вимірюють у системі СГС. Одиницею в'язкості в системі СГС є пуаз (1 П)*: 1 П = 0,1 Па∙с =» 1 Па∙с = 10 П.

У здорової людини в'язкість крові знаходиться в межах 4 — 5 сП, при анемії вона може знижуватись до 2—3 сП, але може й підвищуватися до 18—20 сП (у разі поліцитемії, інфаркту міокарда, гіпертонії тощо). У зв'язку з цим вимірюван­ня в'язкості крові має певне значення при постановці діагнозу, а також у судово-медичній експертизі.

2. У лікувальній практиці в'язкість біологічних рідин , як правило, по­рівнюють із в'язкістю води і називають відносною в'язкістю:

Відносна в'язкість показує, в скільки разів в'язкість певної рідини більша (або менша), ніж в'язкість води.

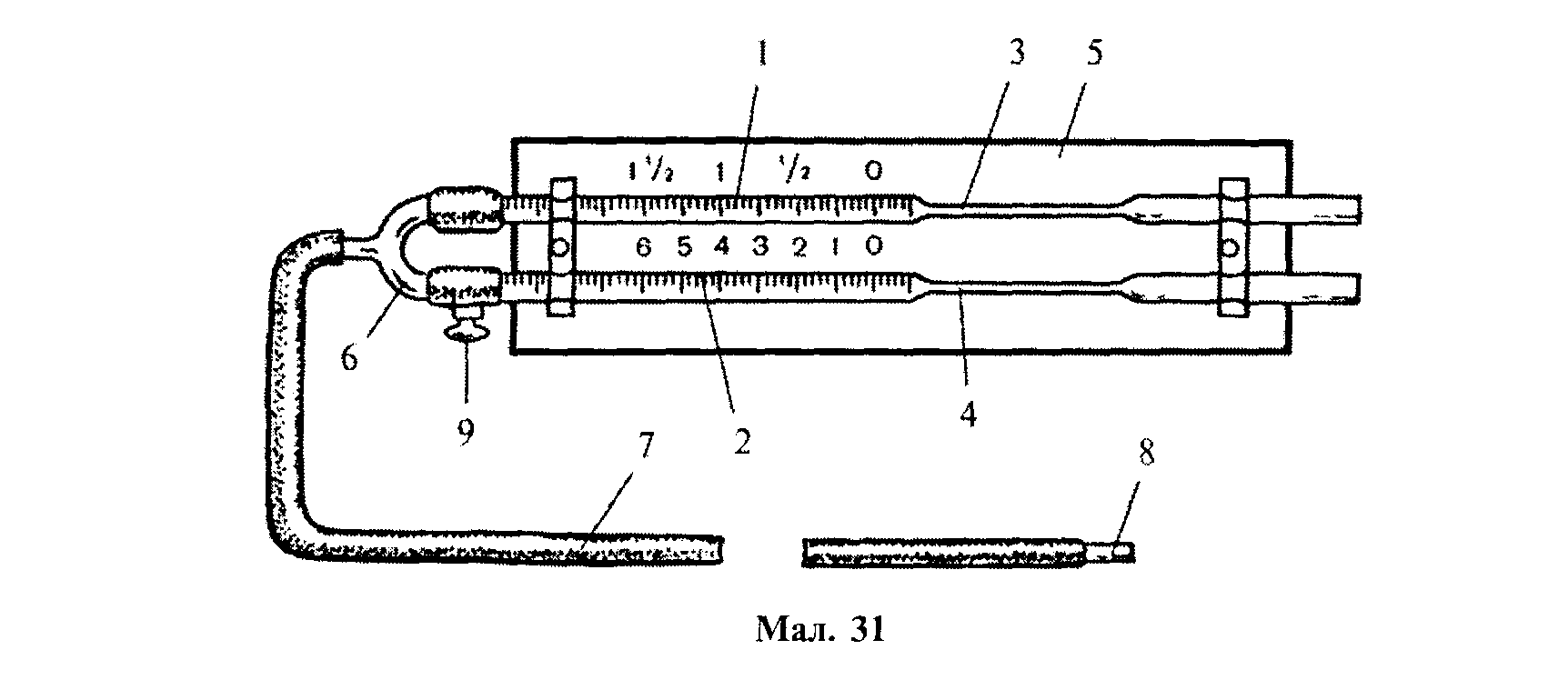
В умовах клініки відносну в'язкість крові вимірюють за допомогою капіляр­ного віскозиметра ВК – 4 (мал. 31). Він складається з двох градуйованих піпеток 1 і 2 з однаковими капілярами (тонкими скляними трубочками) З і 4. Піпетки прикріплені до спільної основи 5. Кінці піпеток з'єднуються між собою трійником 6, від якого відходить гумова трубка 7 зі скляним наконечником 8.

Вимірювання відносної в'язкості крові грунтується на тому, що об'єми води

і крові , які протікають через капіляри віскозиметра, оберненопропорційні їх в'язкостям : Оскільки капіляри віскозиметра однакові, то

і , де S — поперечний переріз капілярів віскозиметра, а і — довжини стовпчиків води і крові в них. Тоді

(4)

Таким чином, вимірювання відносної в'язкості крові зводиться до визначен­ня довжини стовпчиків води й крові в капілярах віскозиметра.

3. Рідини чинять значний опір рухові тіл у них. Сила опору, з якою рідина діє на тіло, що рухається в ній, залежить від багатьох факторів: швидкості, форми й розмірів тіла, а також від в'язкості рідини. Англійський фізик Джордж Стокс (1819—1903) дослідним шляхом визначив (1851) силу опору рідини для найпрос­тішого випадку, коли тіло має форму кулі невеликих розмірів і рухається в рідині з невеликою швидкістю (мал. 32). Згідно із законом Стокса, сила опору, який рідина чинить рухові кулі радіусом R, пропорційна в'язкості рідини η, радіусу кулі R і швидкості її руху :

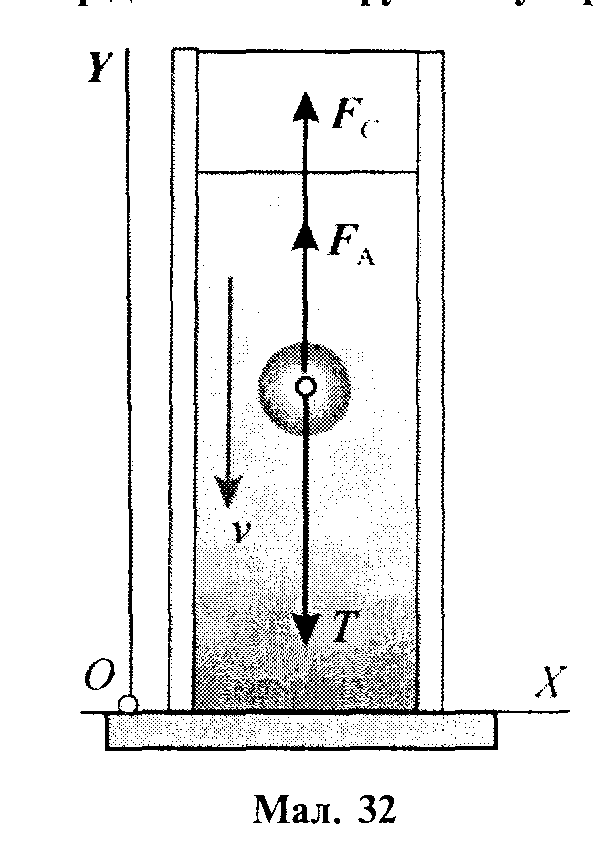
Закон Стокса використовується для визначення швидкості осідання колоїдних частинок у розчинах, крапельок туману в повітрі, еритроцитів у плазмі крові і т. ін. Математичний розрахунок показує, що швидкість падіння кульки радіусом R у рідині (або в газі) в'язкіс­тю л і густиною р. визначається за формулою

де — густина речовини, з якої виготовлена кулька. Якщо на досліді ви значити швидкість падіння кульки в рідині, тоді з формули (2.8) можна знайти в'язкість рідини:

Цим способом визначають в'язкість машинного й трансформаторного масел, мастил, клеїв, лаків та інших високов'язких рідин.

Співвідношення (2.8) використовують в одному з методів діагностики — ре­акції осідання еритроцитів (РОЕ)*. Еритроцити — це без'ядерні клітини діамет­ром 7,5 мкм, що мають форму двоввігнутого диска. Якщо набрати невелику кількість крові в пробірку, то еритроцити почнуть повільно осідати донизу зі швидкістю, що визначається за формулою (2.8). Оскільки радіуси й густина всіх еритроцитів однакові, то швидкість їх осідання залежить від густини й в'язкості крові. При запальних процесах в'язкість крові змінюється, відповідно до цього змінюється й швидкість осідання еритроцитів у плазмі крові. Тому за швидкістю осідання еритроцитів можна судити про наявність запальних процесів в організмі людини. У здорових жінок швидкість осідання еритроцитів коливається в межах 7—12 мм/год, а в чоловіків — 3—9 мм/год.

Законом Стокса користуються і в гігієні для визначення швидкості осідання пилу, частинок диму та інших газотопних відходів виробництва. Розрахунки, ви­конані за формулою (2.8), показують, що пилинки розміром 5—0,2 мкм осідають у повітрі зі швидкістю 0,2—0,0003 см/с. У кімнаті зі стелею заввишки 3 м такий пил повністю осідає приблизно за 12 діб (за умови, що повітря нерухоме).

Розглянемо принцип вимірювання в’язкості за допомогою капілярного віскозиметра.

Капілярний метод базується на використанні формули Гагена – Пуазейля, згідно з якою об’єм рідини V, що протікає за час t через капіляр довжиною l та радіусом R при наявності перепаду тиску Δр на кінцях капіляра. Дорівнює:

V=𝜋R⁴ Δрt/8ηl.

Для вертикального капіляра перепад тиску зумовлений гідростатичним тиском стовпа рідини висотою h, тобто:

Δр=ρgh, де ρ – густина рідини.

За цими формулами знаходять в'язкість рідини:

η= 𝜋R⁴ ρght/8lV.

Враховуючи, що величини V, l, R, h є сталими для даного капіляра, та вводячи сталу віскозиметра

с = 𝜋R⁴gh/ 8lV,

можна визначити значення в’язкості:

η = сρt.

Час протікання досліджуваної рідини через даний капіляр залежить від його параметрів, густини та в’язкості рідини. Вимірюючи цей час для протікання однакових об’ємів досліджуваної (t_х) та еталонної (t_ет) рідин, отримаємо формули, які дозволяють визначити значення відносного η_від. Та абсолютного η_абс. коефіцієнтів в’язкості досліджуваної рідини:

1. η_від.= η_х/ η_абс. = ρ_х t_х/ρ_ет t_ет, (2) η_{х =} η_абс.= η_ет. η_від.

Замість еталонної рідини, як правило, використовують дистильовану воду, в'язкість якої (η_ет.) залежно від температури наведена в таблиці.

Залежність в'язкості дистильованої води від температури.

t0С	ηет.	t0С	ηет.	t0С	ηет.
0	0,00179	21	0,00098	30	0,00080
5	0,00151	22	0,00096	40	0,00065
10	0,00131	23	0,00093	50	0,00055
15	0,00114	24	0,00091	60	0,00047
16	0,00111	25	0,00089	70	0,00041
17	0,00108	26	0,00087	80	0,00036
18	0,00106	27	0,00086	90	0,00032
19	0,00103	28	0,00084	100	0,00028
20	0,00100	29	0,00082	110	0,00026

Практичні завдання.

1.Ознайомтесь з будовою капілярного віскозиметра.

Капілярні віскозиметри Оствальда і Уббелоде:

1. кульовий сосуд для вимірювання об’єму рідини, що протікає через капіляр;

2. капіляр;

3. кульовий сосуд для збирання рідини.

Загальними умовами в методиці роботи з віскозиметрами є суворо горизонтальне або вертикальне встановлення приладу, заповнення сухого і чистого приладу продуктом і його термостатування при вибраній температурі, вимірювання часу витікання певного об’єму, що зумовлений в'язкістю та різницею висот між мітками на капілярі. Перед робочими вимірюваннями прилад тарирують за еталонною рідиною, тобто визначають час її витікання t_ет (дистильована вода, цукровий розчин або касторове масло).

У абсолютних приладів, що не потребують тарировки, константу визначають за розмірами робочих органів у відповідності з рівнянням Пуазейля.

2.Визначіть час протікання через капіляр фіксованого об’єму спочатку дистильованої води

t_ет , а потім досліджуваної рідини t_х

3.Розрахуйте відносну в'язкість за формулою (1), взявши густину дистильованої води

ρ_ет =(1000 ⁺_-1)кг/м³ ,а густину досліджуваної рідини взяти рівною ρ_х = (1120 -⁺ 5) кг/м³.

4.Розрахуйтеабсолютне значення коефіцієнта η_{х =} η_абс за формулою (2), визначивши за наведеною вище таблицею коефіцієнт в'язкості дистильованої води для температури досліду.

5.Знайдіть відносну ε та абсолютну Δη похибки за формулами:

ε = Δη_х/ η_х = Δt_x/t_x + Δt_ет./t_ет + Δ ρ_х/ ρ_х + Δ ρ_ет/ ρ_ет;

Δ η_абс. = ε η_абс.; Δ η_від. = ε η_від.

Кінцевий результат подати у вигляді:

η_х = (η_{абс._}⁺ Δ η_абс.)Па ∙ с; η_від. = (η_{від._}⁺ Δ η_від.).

6.Ознайомтесь з будовою і дією віскозиметра ВК – 4.

Будова його описана вище.

Робота з віскозиметром:

1).Промити капіляри спиртом і просушити за допомогою груші.

2).Відкрити кран 9 і, витягуючи повітря через наконечник 8 за допомогою шприця, набрати дистильовану воду в бюретку 2 до позначки «О».

3).Закрити кран 9 і втягувати через наконечник 8 досліджувану рідину в бюретку 1 до позначки «О».

4).Відкрити кран 9, втягувати повітря через наконечник 8, поки рівень досліджуваної рідини в бюретці 1 не дійде до позначки «1» (L = 1). Вода при цьому досягає в бюретці 2 другої позначки L_ет..

Як видно із формули (4), відносний коефіцієнт в'язкості досліджуваної рідини за цих умов чисельно дорівнює L_ет.

Контрольні запитання.

1.Чим обумовлена в'язкість рідини та від яких параметрів вона залежить?

2.Що таке ньютонівська та не ньютонівська рідини?

3.Дайте визначення коефіцієнта в'язкості та вкажіть одиниці його виміру.

4.В чому полягає різниця між ламінарним та турбулентним плином рідин?

5.Від яких умов залежить в'язкість крові?

6.Задача №1.

Визначіть об’ємну та лінійну швидкості плину рідини, якщо діаметр судини 3 см, відносна в'язкість дорівнює 2, густина 1000кг/м³, число Рейнольдса дорівнює 3000.

7.Задача №2.

У рицинову олію занурили сталеву кульку діаметром d = 1мм і визначили, що відстань 5см вона пройшла за 14,2с. Вважаючи рух кульки рівномірним, визначіть в'язкість рицинової олії. Густина олії 960кг/м³, а густина сталі 7860кг/м³.(1,07 10^-4 Пуаз).

8.Задача №3.

В артеріолі діаметром 2,5∙10^-5м рухається потік крові із швидкістю 2,8∙10^-3м∙с^-1. Чому дорівнює різниця тисків Δр на кінцях артеріоли, якщо її довжина становить 5∙10^-3м? В’язкість крові 4,5∙10^-3Па∙с (застосуйте закон Гагена – Пуазейля Δр = 8∙V∙η∙l/𝜋∙R⁴). (3200 Па)

Практична робота № 1.

Тема: «Визначення реологічних властивостей крові».

Мета роботи: вивчити реологічні властивості крові, визначення швидкості кровоплину, використання різних методів вимірювання тиску крові, визначення швидкості поширення пульсової хвилі, визначення видів течій рідин; розглянути правила дотримання протиепідемічного режиму в практичній діяльності, правил техніки безпеки, питання охорони праці в галузі.

Потрібне приладдя: тонометри, відеофільм, таблиці.

Теоретичні відомості.

Кров являє собою суспензію форменних елементів ( еритроцитів, лейкоцитів) в плазмі. Концентрація еритроцитів в крові складає (4 – 6 )10⁶мм^-2,лейкоцитів – (4 – 10)10³мм^-3, тромбоцитів – (1,5 – 3)10⁵мм^-3.

Озн. Гематокрит – це частина об’єма крові, що приходиться надолю еритроцитів. Внаслідок малої концентрації лейкоцитів і тромбоцитів (сумарний об’єм складає приблизно 1 %),вони несуттєво впливають на механічні властивості крові, порівняно з еритроцитами. Кров теоретично розглядається як суспензія еритроцитів в плазмі.

Вплазмі 900 – 910г/л води, 65 – 80г/л білків ( альбумін, глобулін, фібриноген) і 20г/л низькомолекулярних з’єднань. Вцілому плазма – ньютонівська рідина, хоча є незначні відхилення через вміст білків. В’язкість 1,9 – 2,3 сПз.

Плин крові , в основному, ламінарний і тільки в деяких випадках переходить в турбулентний: в проксимальних відділах аорти та легеневого стовбура під час систоли, в крупних артеріях при зростанні швидкості провоплину під час інтенсивної м’язової роботи або при зниженні в’язкості при анемії.

Тиск і швидкість кровотока.

Згідно теореми про нерозривність струменя, швидкість обернено пропорційна площі поперечного перерізу. Аорта розділяється на артерії, артерії – на артеріоли, потім на капіляри. Кожне розгалуження супроводжується зменшенням діаметра окремих судин і збільшенням сумарної площі поперечного перерізу всіх судин даного класу.

Самим вузьким відділом судинного русла є аорта, тому швидкість крові в ній максимальна і знижується у напряму до капілярів. Сумарна площа перерізу капілярів в 500 – 600 разів більше площі аорти. Значне зниження швидкості кровотоку в капілярах сприяє покращенню обміну речовин між кров’ю і тканинами. В венах швидкість знову зростає.

Основною рушійною силою кровотока є кров’яний тиск, зумовлений перевищенням тиску, обумовленного роботою серця, над атмосферним тиском.

Розподіл тиску крові в судинній системі з деяким наближенням описується формулою Пуазейля:

Q = 𝜋R⁴ Δp/8ηl = Δp/Х,

де Х = 8ηl/ 𝜋R⁴ – гідравлічний опір.

Враховуючи, що радіуси просвітів аорти R_аор, артерій R_арт, артеріол R_арл та капілярів R_кап відносяться, як:

R_аор: R_арт: R_арл: R_кап= 3000 : 500 : 7 : 1,

то мінімальний гідравлічний опір – у аорти, а максимальний – у капіляра. Але всі судини даної частини кровообігу ввімкнені в ток крові паралельно, тому їх сумарний опір:

= + + …, де Х₁, Х₂ , …- гідравлічні опори кожної судини даного відділу системи кровообігу. Тому чим більше судин даного типу в організмі, тим в більшій степені сумарний опір менше опору однієї судини. Завдяки великій кількості капілярів сумарний опір капілярної мережі менше сумарного опору артеріол, а тим паче аорти.

Найбільший гідравлічний опір серед всіх ділянок судинної системи має сукупність артеріол. Зміна їх перерізу відіграє головну роль в регуляції тиску крові. За формулою Пуазейля чим більше гідравлічний опір, тим більше спадає тиск на ділянці, тобто тим більшу силу треба прикласти для проштовхування крові по судинам. Згідно експериментальних даних падіння тиску в крупних і середніх артеріях складає 10%, в артеріолах і капілярах – 85%, тобто 85% енергії, що надається крові при скороченні шлуночка, іде на просування крові по артеріолах і капілярах.

Т. я. зі збільшенням радіуса судини опір зменшується, то навіть незначна зміна радіуса впливає на величину кров’яного тиску. Тому природні механізми нервової і гуморальної регуляції тиску крові, а також дія лікарських препаратів, що нормалізують тиск, зв’язані зі зміною просвіту судин.

Насправді, через еластичність судин, відхилення від ламінарності течії крові та інші причини, гідравлічний опір більший за теоретично розрахований.

Пульсова хвиля.

Озн. Ударний об'єм крові – це об'єм, який виштовхується в уже заповнену аорту або легеневий стовбур при скороченні лівого та правого шлуночків:

V = 60 – 70 мл.

Озн. Фаза скорочення м’яза серця – систола, розслаблення – діастола. В систолу кров вштовхується в аорту, в діастолу – аорта, скорочуючись, проштовхує кров далі.

Озн. Систолічний тиск – це максимальний тиск в аорті після подання в неї ударного об’єму крові:

СТ = 120 мм рт. ст.

Діастолічний тиск – тиск в аорті, перед вштовхуванням ударного об’єму:

ДТ = 80 мм рт. ст.

120/80 – артеріальний тиск.

Під час систоли кров викидається із лівого шлуночка в аорту і артерії. При цьому частина кінетичної енергії крові витрачається на розтягування еластичних стінок судин і запасається у виді потенціальної енергії пружніх деформацій. Під час діастоли шлуночків аортальний клапан закривається і перехід крові від серця до судин припиняється. Розтягнуті стінки артерії при цьому скорочуються, забезпечуючи рух крові до капілярів.

Вперше ідея про такий засіб руху крові висунута сільським священником Хейлсом у 1733 році. В 1899р. Франк створив гідродинамічну модель кровотока. Розтягнені стінки судини стискаються і повертаються в стан рівноваги, проштовхуючи при цьому кров далі вздовж русла і викликаючи розтягнення слідуючої ділянки судини. Цей процес продовжується, поступово затухаючи, до кінцевих розгалуджень артерій і артеріол, де пульсуючий кровоток змінюється неперервним. Таким чином , по судинам розповсюджуються коливання тиску.

Озн. Пульсова хвиля – це розповсюдження вздовж артерій коливань тиску, які виникають в аорті після викидання в неї ударного об’єму крові.

Швидкість розповсюдження пульсової хвилі знаходиться за формулою:

υ = , h – товща стінок сосудів,

d – їх внутрішній діаметр,

ρ – густина крові,

Е – модуль пружності.

З віком Е зростає, тому швидкість зменшується, за швидкістю можна встановити Е.

Швидкість пульсової хвилі 6-12 м/с, в 20-40 разів більше швидкості кровоплину (0,3 - 0,5 м/с). Так, пульсова хвиля досягає стопи за 0,2 с., а частинки крові за цей час дойдуть до кінця аорти.

Вимірювання тиску за методом Короткова.

На плече надівають манжетку, нагнітають повітря до стискання аорти. Плин крові припиняється. Краном повільно випускають повітря з манжети. Коли тиск досягає систолічного – кров починає пробиватись через аорту і виникає складне явище – флаттер (сумісні автоколивання стінок і потоку крові), що викликає звук, який фіксується фонендоскопом. При досягненні діастолічного тиску автоколивання припиняються.

Сфігмотонометр – з мембранним манометром;

сфігмоманометр – з ртутним манометром.

Практичні завдання.

1.За допомогою тонометра виміряйте тиск один у одного. Запишіть отримані результати.

2.Розв’яжіть задачі:

1). Середня швидкість кровотока в аорті складає 0,45м/с, а в капілярах – 0,5мм/с. В скільки разів площа поперечного перерізу аорти менше суми поперечних перерізів капілярів?

2). Визначіть гідравлічний опір Х аорти, якщо її діаметр складає 2,4см, довжина 40см, в’язкість крові 5сПз.

3). Швидкість розповсюдження пульсової хвилі по артерії складає 10м/с. Визначіть модуль пружності артерії, якщо товща її стінки 0,7мм, внутрішній діаметр 8мм, густина крові 1050кг/м³.

4). Внаслідок розвитку атеросклерозу коефіцієнт пружності аорти зріс в 1,8 разів, при цьому , за рахунок відкладання холестерину в аорті пацієнта, товща її стінки збільшилась в 1,5 разів, а внутрішній діаметр зменшився на 25%. Яку зміну швидкості пульсової хвилі зафіксує сфігмометр?

Контрольні запитання.

1. Охарактеризуйте склад крові.

2. Якою є течія крові?

3. Охарактеризуйте в’язкість крові в різних ділянках судинної системи.

4. Охарактеризуйте гідравлічний опір різних ділянок судинної системи.

5. Поясніть фізичні основи вимірювання тиску за методом короткова.

6. Що таке пульсова хвиля?

7. Як зв’язана швидкість розповсюдження пульсової хвилі зі станом судинної системи?

Самостійна робота №4.

Тема: «Загальні поняття термодинаміки».

Марц. р.3 ст.142-150.

Питання.

1.Означення термодинаміки.

2.Означення термодинамічної системи, 3 види систем.

3.2 розділи термодинаміки.

4.Означення термодинамічної рівноваги.

5.Два закони класичної термодинаміки.

6.Поняття ентропії.

7.Означення стаціонарного стану системи, приклад.

8.Чи виконуються І і ІІ закони термодинаміки для живих організмів?

9.Означення спряження і спряжених процесів, приклади, теорема Пригожина.

10.Поняття сінергетики.

Теоретичний матеріал до роботи.

Основні положення рівноважної термодинаміки .

Озн. Термодинаміка - розділ фізики, в якому розглядаються процеси (теплові явища) з самих загальних позицій, тобто без врахування мікроскопічної будови тіл.

Озн. Тіло, або група тіл, які взаємодіють з середовищем шляхом обміну речовиною або енергією через роботу та теплоту, називається термодинамічною системою.

Середовище - це всі тіла, які оточують систему і не входять до її складу.

Термодинамічні системи діляться на три види:

Ізольовані - ті, що не обмінюються з навколишнім середовищем ні речовиною, ні енергією.

Закриті – обмінюються з середовищем енергією, але не речовиною.

Відкриті - обмінюються і речовиною, і енергією.

Ізольованих систем не існує.

Термодинаміку ділять на 2 розділи:

класичну (рівноважну) і 2) термодинаміку необоротних процесів (нерівноважну). Остання застосовується для біологічних процесів.

Озн. Термодинамічна рівновага - це такий стан системи, при якому термодинамічні параметри не змінюються з часом. Якщо параметри змінюються, то це процес ( параметри –це величини, які характеризують стан системи - P, T, V, …).

Класична термодинаміка.

I закон термодинаміки:

теплота, передана системі, витрачається на приріст внутрішньої енергії системи і на виконання системою роботи:

Q = ∆U + A^ﺍ

Озн. Процес називається оборотним, якщо він може бути проведений у зворотньому напрямку через ті ж стани, що і при прямому процесі, без витрат енергії зовні.

II закон: любий реальний процес є необоротним.

I закон виконується завжди, а II має ймовірнісний характер (ймовірність переходу тепла від холодного тіла до гарячого 1:10³⁰⁰).

Поняття ентропії.

Ентропія – це функція стану системи, яка вказує, як далеко перебуває система від свого стану рівноваги( від грецького „повертаюся всередину”).

Нехай при деякій температурі Т тіло отримало (або віддало) кількість теплоти Q, тоді називається зведеною теплотою.

Клаузіус показав, що зміна ентропії тіла дорівнює:

∆S = S₂ - S₁=

Якщо тіло отримує енергію, то Q>0 і ∆S>0 – ентропія зростає і навпаки.

Приклад:

Підрахувати зміну ентропії при плавленні 18 кг льоду (λ=3,35 · 10⁵Дж/кг):

∆S = S₂ - S₁= = = 2,2 · 10⁴Дж/К .

Якщо температура змінюється, то розіб’ємо процес на велику кількість елементарних процесів, щоб на кожній з них температура була приблизно сталою, тоді:

∆S= ∑ .

Доведено , що при оборотних процесах ентропія не змінюється (∆S = 0), а при необоротних - зростає (∆S>0). Таким чином в замкненій системі ентропія не може зменшуватись: ∆S≥0 - це також II закон термодинаміки.

І ще: ентропія – це міра безладдя в системі . Згідно II закону у замкненій системі безладдя може тільки зростати. Найбільшою буде ентропія у стані теплової рівноваги.

( Принцип Больцмана- ст.145-146).

В термодинаміці розглядається поняття теплового двигуна. Теплові двигуни грають велику роль в житті людини і забруднюють навколишнє середовище. Тому проблема полягає в відшуканні меньш «брудних» джерел енергії.

Положення нерівноважної термодинаміки.

Кожна клітина і організм вцілому є відкритими системами і тільки в окремих частинах клітини є умови для закритих і ізольованих систем. Процеси, що протікають в біосистемах, необоротні.

Якщо для класичної термодинаміки фундаментальним поняттям є поняття рівноважного стану, то для живого організму такий стан неприпустимий, так як тоді неможливі ніякі процеси. І основним поняттям є стаціонарний стан.

Озн. Стаціонарний стан – це такий стан системи, в якому параметри не змінюються з часом, але в різних частинах системи можуть відрізнятися, тобто в таких системах існують і постійно підтримуються градієнти параметрів. Це можливо тільки за рахунок потоку енергії або речовини з оточуючого середовища.

Приклад: стаціонарний стан різної концентрації іонів Na⁺ і К⁺ по обидві боки від клітинної мембрани у стані спокої, яка підтримується за рахунок Na – К насосів, що працюють на енергії молекул АТФ.

Звичайно, живі організми постійно розвиваються і тому вцілому не є стаціонарними системами, але протягом невеликого часу стан їх частин є стаціонарним.

I і II закони виконуються для цієї термодинаміки. Існування живих організмів в нерівноважному стані потребує притоку енергії. Тварини в якості джерела енергії застосовують їжу, точніше, хімічну енергію їжі. У 1780р. Антуан Лавуазьє и П’єр Лаплас довели справедливість I закону термодинаміки для біологічних об’єктів. Вони виміряли кількість теплоти і вуглекислого газу, що виділяються морською свинкою у процесі життєдіяльності, і порівняли ці величини з тепловим ефектом реакції спалення споживаних продуктів до СО₂. Отримані результати показали рівність внутрішньої енергії продуктів споживання і виділеної енергії.

Що стосується II закону, то можливі 3 ситуації:

рівень організації системи зменьшується;

не змінюється (стаціонарний стан);

зростає.

У 2 і 3 ситуації ентропія не змінюється, або зменшується, але насправді

загальний енергообмін живих організмів відбувається так: сонячне світло, поглинене рослинами, енергетично забезпечує синтез вуглеводів з Н₂О і СО₂ (фотосинтез). Окислення вуглеводів у процесі дихання супроводжується виділенням енергії, яку використовують для своєї життєдіяльності рослини і тварини. Поглинання світла викликає зниження ентропії в живому організмі, але одночасно іде підвищення ентропії на Сонці в процесі ядерних реакцій на більшу величину. Вцілому в системі Земля-Сонце ентропія зростає.

Таким чином розвиток живих організмів відбувається за рахунок зменшення упорядкованості оточуючого середовища.

Спряжені процеси.

В процесі функціонування біологічних систем відбуваються як процеси з виділенням енергії (Q<0), так і з поглинанням (Q>0).

Озн. Явище, при якому один процес енергетично забезпечує протікання другого, називається спряженням, а процеси – спряженими.

Приклад.

Найбільш розповсюдженою спрягаючою (енергія виділяється) реакцією в живих організмах є реакція гідролізу АТФ:

АТФ + Н₂О → АДФ + Ф + Q ( 30,5кДж/моль).

^фосфат

АТФ-аденозинтрифорфорна кислота.

Ця енергія іде, наприклад, на реакцію гліколізу:

глюкоза + Ф = глюкоза – 6 фосфат + Н₂О, для якої потрібно 13,4кДж/моль.

Явища спряження знижують витрати енергії у виді тепла.

Лінійна нерівноважна термодинаміка вивчає процеси, що протікають поблизу термодинамічної рівноваги. Можна показати, що в цих умовах між швидкістю процесу J (загальним потоком) та рухаючою силою Х (причиною процесу), що його викликає, існує лінійна залежність:

J = L · Х, L – коефіцієнт пропорційності.

Приклад: закон Ома: J = · U

Рухаюча сила – напруга U;

поток – електричний струм J;

коефіцієнт пропорційності – -провідність.

При спряжених процесах не вся енергія, що виділяється, передається спряженому процесу: частина переходить в тепло.

Вводиться поняття ефективності спряження: для біологічних процесів вона 80-90%.

Теорема Пригожина:

В стаціонарному стані швидкість зростання ентропії, обумовленого протіканням необоротних процесів, має позитивне і мінімальне з можливих значень.

У живих організмів є механізм аутостабілізації, наприклад, підвищення t^о тіла людини веде до збільшення тепловіддачі і зменшення теплопродукції.

Сінергетика.

Творець - німецький професор Герман Хакен. Термін переводиться, як «разом дія».

Озн. Момент якісної зміни системи називається біфуркацією.

Сінергетика пояснює процес еволюції: любий об’єкт є системою, тобто сукупністю елементів і зв’язків між ними.

Елементи системи завжди мають деяку самостійність поведінки, рух елементів на мікрорівні – це так звані флуктуації (тобто малі, незначні процеси). Між елементами системи є колективні взаємодії. Найчастіше ці колективні взаємодії подавляють мікрорухи елементів- тоді кажуть про негативні зворотні зв’язки. Таке об’єднання елементів буде стійке, стабільне.

Але при певних зовнішніх умовах характер колективної взаємодії може радикально змінитися: головну роль починають грати такі колективні взаємодії, які підсилюють індивідуальні рухи елементів. Флуктуації підсилюються і це може привести до нової організації в системі. Момент якісних змін називається біфуркацією. Біфуркації описуються відповідними розділами математики – теорією катастроф.

Тема №3.

«Електричні властивості клітин, тканин і органів та деякі методи реєстрації медичної і біологічної інформації».

Лекція №3.

Тема: «Електричні властивості клітин, тканин і органів та деякі методи реєстрації медичної і біологічної інформації».

Література: М. гл.4.3, 5.1 – 5.3.

Ш. розділ 10, 11, 17, 22.

Біопотенціали.