Задачі до олімпіади разом 11 02 2014

Кут висоти полярної зірки – широта місцевості.

Задача

Полярну зірку видно під кутом 50° 30' , довгота 30° 30' сх.д. Координати точки 50° 30' пн. ш. 30° 30' сх.д. ( Київ ).

Задача

Полярна зірка на рівні горизонту : екватор – широта 0. Полярна зірка в зеніті – точка – Північний полюс.

Задача № 5. Місто розташоване на 39 сх.д., а полярну зірку видно на відстані 81⁰ від точки зеніту.

90° - 81° = 9° пн. ш. Координати точки 9° пн ш 39° сх д Адіс – Абеба

Точки – антиподи

І варіант – по діаметру паралелі А Біла Церква 50° пн. ш 30° сх. д А₁ - протилежна по діаметру паралелі.

30° сх. д - 180° д = 150° зх. д

А Львів 49° 50' пн. ш. 24° сх. д антипод = А₁ 49 °50' пн ш ( 24° сх д – 180° = 156 °з д)

ІІ варіант – антипод діаметрально протилежна точка земної кулі( по діаметру Землі)

Точка А Біла Церква = 50° пн ш 30° сх д Точка А₁ 50° ПД Ш (30° сд – 180° д = 150° зх д ) ==== 50° ПД Ш 150° зх д

9. Тільки широта … у полюсів – 90° пн ш ; 90° пд.ш 10. Тінь на північ – Південний полюс.

11.Будь який напрямок на: Південному полюсі – тільки на північ та навпаки.

Задача № 16 Які меридіани слугують продовженням 30 сх. д, 80 сх. д; 160 зх. д. Літаки летять над цими меридіанами на північ і перетинають Північний поюс, продовжуючи політ вздовж меридіана . ( див. задачі по антиподах).

30 °сх д – 180°д = 150° зх. д 80°сх д – 180° = 100° зх д 160° зх д – 180° = 20 °сх д

Задача № 17 Якщо проткнути глобус шпицею у місті Києві через центр Землі, яка точка вийде ( антиподи

ІІ варіант). Київ 50° 30' пн ш 30°

30' сх д = антипод 50° 30 ' пд ш ( 30° 30 ' сх д – 180°) = 149 °30' зх д = 50° 30' пд ш 149° 30' зх д

Форма та розміри Землі

Земля сплющена біля полюсів . Довжина дуги 1^о меридіана найменша на екваторі 110,6 км, збільшується до полюсів . 0°- 14° = довжина дуги 1° меридіана – 110, 6 км, 15° – 22° – 110. 7 км …. 78° – 89° – 111, 7 км

Задача № 20 Визначте довжину дуги 1° екватора === екватор – 40 075. 75 км, а це 360 °, отже

40 075. 75 км : 360° = 111,3 км.

Задача № 21 Визначте довжину дуги 1° меридіана == Коло меридіана 40 008,5 : 360° = 111,1 км.

Довжина дуги паралелі зменшується від екватора до полюсів.

0 °– 111,3 км, 30 °– 96,4 км, 60° – 55, 8 км, 90° - 0 км ( полюс)

Задача Літак здійснює кругосвітню подорож : а) по екватору; б) по 40° паралелі; в) по північному тропіку.

а) по екватору = 1° дуги паралелі – 111, 3 км Х 360 = 40 076 км.

б) по тропіку = 102, 8 км Х 360 = 37 008 км

в)по 40° = 85, 4 км Х 360 = 30 742 км

Задача Санкт – Петербург та Київ на одному меридіані . 21 березня сонце в С- П на висоті 30 , в Києві на 39 30 . Знайти відстань між містами в км, градусах.

39 °30' - 30' = 9° 30 , довжина 1° меридіана 111,1 км === 9° 30' Х 111,1 = 1055 км.

Дальність видимого горизонту

Кулястість Землі приводить до горизонту, з збільшенням висоти дальність видимості горизонту збільшується. L( дальність видимого горизонту) = 3,83 Х √h( висота спостерігача); 3,83 – дальність видимого горизонту з висоти 1 м.

Задача Ви піднялися на найвищу вершину Кримських гір. Як далеко ви бачите навколо себе?

Розв'язання: найвища, точка Кримських гір, вершина Роман - Кош, має висоту 1545 м. Використовуючи формулу для визначення

дальності видимого горизонту L = 3,83 -Jh , робимо розрахунки:

L = 3,83 х √1545 = 3,83 х 39,3 = 150,5 км.

Відповідь: дальність видимого горизонту з найвищої точки Кримських гір становить 150,5 км.

Обчислення відстаней за градусною сіткою

Меридіани вказують на довготу, паралелі – на широту.

Існують Північна та Південна півкулі, Західна та Східна півкулі.

Довжина дуги в 1° будь-якого меридіана (бо всі меридіани мають однакову довжину) дорівнює 111,1км ≈ 111 км

Обчислення відстаней у градусах і кілометрах за градусною сіткою

Задача 33. Визначте координати крайніх точок Африки та протяжність материка із заходу на схід по 10° пн. ш. та з півночі на південь (у градусах і кілометрах).

Розв'язання:

1) Визначаємо на 10-й паралелі крайні точки материка. Вони лежать на таких довготах: західна (місто Конакрі) - 13° зх. д., східна (мис Рас-Гафун) - 52° сх. д.;

2)знаходимо протяжність території в градусах: (оскільки точки розташовані по обидві сторони від нульового меридіана, то значення знайдених координат потрібно додати):

13° зх. д. -+ 52° сх.д. = 65°;

3)за табл. 2 або за атласом, визначаємо, що на 10" пн. ш. довжина дуги 1° паралелі становить 109,6 км, і знаходимо протяжність території у кілометрах:

65° х 109,6 км = 7124 км;

4) далі визначаємо протяжність материка з півночі на південь у градусах. Для цього необхідно визначити географічну широту крайніх північної і південної точок материка. Північна точка - мис Рас-Енгела - 37° нгі. ш., а південна - мис Агульяс (Голковий)- 35° пд. ш. Оскільки точки розташовані по обидва боки від екватора, то значення знайдених точок потрібно додавати: 37° + 35° = 72° (протяжність материка у градусах);

знаючи, що значення дуги 1° меридіана дорівнює 111,1 км, визначаємо протяжність материка у кілометрах: 72°х111,1 км = 7992 км.

Відповідь: протяжність материка із заходу на схід по 10° пн. ці, становить 65°, або 7124 км, а з півночі на південь 72°, або 7992 км.

Задача 34. Визначте відстань у градусах і кілометрах від Києва до: а) екватора; б) Південного полюса; в) Північного тропіка.

Розв'язання: а) географічна широта Києва приблизно 51° пн. ш., а екватора - 0°. Отже, відстань від Києва до екватора у градусах становитиме 51° (51° - 0° = 51°), а у кілометрах - 5666 км (51°х 111,1 км = 5666 км);

географічна широта Південного полюса - 90° пд. ш. Відстань від Києва до Південного полюса у градусах становитиме 141° (51° + 90° = 141°). Дані значення потрібно додавати, оскільки об'єкти знаходяться по різні сторони екватора. Далі визначаємо відстань у кілометрах:

141° х 111,1 км = 15665 км;

в) географічна широта Північного тропіка - 23°27' пн. ш. Відстань між ними у градусах буде становити приблизно 27,5°, а у кілометрах - 27,5° х 111,1 км = 3 055 км.

Відповідь: відстань від Києва до екватора 51°, або 5666 км; до Південного полюса - 141°, або 15665 км; а до Північного тропіка - 27,5°, або 3055 км.

** Приклад

Визначте приблизну площу країни, якщо відомо, що вона лежить на 60º пн.ш. і витягнута по широті на 3°, а по довготі - на 4°.  Витягнутість по широті означає вздовж меридіана. Довжина дуги в 1° меридіана дорівнює 111 км. Витягнутість по довготі означає вздовж паралелі. Довжина дуги 1° паралелі на широті 60° дорівнює 111: 2 = 55,5 км. Розв’язання:

S= a*b (111 км*3º) * (55,5 * 4°) = 333 км*222 км = 73 926 км2.

** Приклад

На карті відстань між паралеллю 54° і паралеллю 56° складає 8,9 см. Визначте масштаб карти. Масштаб карти можна визначити, узявши відношення довжини відрізка заміряного на карті, до відповідної відстані на земній поверхні. Відстань за меридіаном у 2градуси (56 - 54) на земній поверхні складає:.

111,2*2 = 222,4км = 22 240 000 см.  М= Lк / Lз = 8.9см / 22 240 000 см.  У чисельному масштабі: 22 240 000 / 8.9=2 498 876.4 або 2 500 000 Відповідь: масштаб карти 1: 2500000.

Добовий рух Землі 3.1. Кутова й лінійна швидкості

Обертання Землі навколо своєї осі відбувається із заходу на схід і, як будь-який обертальний рух, характеризується кутовою і лінійною швидкостями. Кутова швидкість (ω) однакова для всіх широт і становить 15°/год, або 15 "/сек., це можна визначити за формулою:

Ω =360° : 24год = 15 /год., або ω = (360x60x60 ): ( 24x60x60) = 15 /сек.

Лінійна швидкість (V) - це величина, яка показує, з якою швидкістю рухається та чи інша точка земної кулі на тій чи іншій паралелі. Якщо відома довжина паралелі обертання, то лінійну швидкість визначають за формулою:

V = L /t,

де L - довжина паралелі обертання; t - час повного оберту Землі навколо своєї осі (24 год).

Наприклад, нам потрібно визначити лінійну швидкість обертання Землі навколо осі на екваторі, тобто з якою швидкістю рухаються точки, що розта­шовані на екваторі. Оскільки лінійну швидкість визначають в м/сек, то для цього необхідно довжину екватора, виражену в метрах, поділити на час (24 год), виражений у секундах.

V₀ = 40086x1000 : 24x60x60 = 464, м / сек

Отже, лінійна швидкість точок, що розташовані на екваторі, становить 464 м/сек.

Лінійна швидкість - величина змінна. У міру збільшення географічної широти вона зменшується. Цю залежність можна прослідкувати за формулою:

V„ = V₀ х cos ф,

де V_n - лінійна швидкість на певній паралелі; V₀ - лінійна швидкість на екваторі; ф - географічна широта. Наприклад, нам потрібно визначити лінійну, швидкість обертання Землі навколо осі на 60-й паралелі. Відомі нам дані підставляємо в формулу, пам'ятаючи, що косинус будь-якої паралелі можна визначити за чотиризначними математичними таблицями В.М. Брадіса, або за допомогою спеціальних калькуляторів, у яких є функція визначення даного значення.

Vn= 464 х cos 60° = 464 х 0,5 = 232 м/сек.

Отже, на 60-й паралелі лінійна швидкість обертання Землі навколо своєї осі дорівнює половині лінійної швидкості обертання на екваторі.

Визначають лінійну швидкість через кутову:

V= ω R„,

де ω - кутова швидкість; Rn - радіус паралелі обертання, лінійну швидкість якої необхідно визначити.

Радіус паралелі обертання на кожній паралелі буде різним, тому його визначають за формулою:

Rn = R₀ х соs ф.

де R - екваторіальний радіус (6378,24 км); ф - географічна широта.

3.2. Приклади розв'язування задач на визначення кутової та лінійної швидкостей

Задача 35. Визначте лінійну швидкість обертання Землі навколо осі на паралелі 23° 30'; 40°; 66°30\ 90°.

Розв'язання: використовуючи формулу Vn = V0 х cos ф, визначаємо лінійну швидкість обертання Землі навколо осі на заданих паралелях.

На паралелі 23° 30': Vn = 464 x cos 23° 30' - 464 * 0,9170 = 425,5 м/сек;

на паралелі 40°: Vn = 464 x cos 40° = 464 x 0,7660 = 355,4 м/сек;

на паралелі 66°30': V„ = 464 x cos 66° 30' = 464 x 0.3987 = 185 м/сек;

на паралелі 90°: Vn = 464 x cos 90° = 464 x 0 = 0 м/сек.

Відповідь: лінійна швидкість обертання Землі навколо осі на 23° 30' становить 425,5 м/сек; на 40° - 355,4 м/сек; на 66°30'- 185 м/сек; а на 90° - 0 м/сек.

Задача 36. Визначте, з якою лінійною швидкістю рухається точка земної поверхні, на якій розташований Київ, під час добового обертання Землі.

Розв'язання: за допомогою географічної карти визначаємо паралель, на якій розташоване місто Київ. Це буде 50° 30' пн. ш. Отримані дані підставляємо в формулу:

V,, = V_n х cos ф , звідси Vn = 464 х cos 50° 30' = 464 х 0,6361 = 295 м/сек.

Відповідь: точка земної поверхні, на якій розташований Київ, під час добового обертання Землі рухається з лінійною швидкістю 295 м/сек.

Місцевий, поясний і літній час

Обертаючись навколо своєї осі у напрямі із заходу на схід, Земля за добу робить один оберт. Сонце послідовно освітлює всю поверхню земної кулі. Тому, коли на Гринвіцькому меридіані полудень, то на довготі 180° - північ, на довготі 90° сх. д. - вечір, а на довготі 90° зх. д. - ранок.

Місцевий час - це час меридіана даного місця. Що визначається положенням Сонця. Земля робить повний оберт навколо своєї осі за 24 години, тобто будь-яка точка, що розташована на її поверхні, проходить коло довжиною 360°. Отже, за годину Земля повертається на 15°:

360°: 24 год = 15°/год. На 1° Земля повертається за 4 хв (60 хв : 15° = 4 хв або 24 год : 360° = 4хв).

Поясний час - це місцевий сонячний час середнього основного географічного меридіана даного часового поясу, тобто того меридіана, що проходить посередині певного поясу і відрізняється від сусідніх меридіанів на 15°. За міжнародною угодою поверхню Землі умовно поділили на 24 часових пояси (від нульового до 23-го). У межах поясу відлік часу ведуть за тим меридіаном, який проходить посередині. Наприклад, меридіан 15° сх. д. є середнім для першого часового поясу (15 : 15 = 1); 30° сх. д. - для другого (ЗО : 15 = 2); 120° сх. д. - для восьмого (120 : 15 = 8) і т. д.

Відлік часових поясів ведеться від нульового (Гринвіцького) меридіана, а початок нової доби - на 180-му меридіані. Його ще називають лінією зміни дат.

Саме від цієї лінії починається відлік нової доби, яка ніби рухається із сходу на захід. Якщо рухатися у цьому напрямку і перетнути лінію зміни дат, то одна доба додається. Наприклад, після 1 квітня настає 2 квітня. А якщо рухатися у зворотному напрямку, то одну і ту саму добу ми відлічуємо двічі. Наприклад, після 1 квітня знову буде 1 квітня.

Для повнішого і раціонального використання світлової частини доби та економії електроенергії у літній період (з кінця березня по кінець жовтня) стрілки годинників переводять на одну годину вперед. Це так званий літній час. Він діє й на території України.

Задачі на визначення місцевого часу

Задача . За місцевим часом у Миколаєві 12 год 06 хв. Котра година в даний момент за місцевим часом у Києві?

Розв'язання: Визначаємо географічну довготу міст: Миколаїв - 32° сх. д.; Київ - 30° ЗО' сх. д.;

1) визначаємо різницю довготи:

32° сх. д. - 30° 30'сх. д. = 1° 30'; визначаємо різницю в часі: 1° ЗО' х 4 хв = 6 хв;

визначаємо місцевий час у Києві. Київ розташований на за­хід від Миколаєва, тому час буде меншим:

12 год 6 хв - 6 хв = 12 год.

Відповідь: місцевим час у Києві - 12 год.

Задача 47. Місцевий час у м. Біла Церква (30° сх. д.) - 12 год. Визначте, на якому меридіані буде:

а) 15 год; б) 14 год 15 хв; в) 5 год 30 хв.

Розв 'язання:

а) 1) 15 год - 12 год = 3 год; 3 год х 15°/год = 45°; 30° сх. д. + 45° - 75° сх. д.

б) 1) 14 год 15 хв - 12 год = 2 год 15 хв або 135 хв;

2) 135 хв : 4 хв = 33,75° = 33°45', або 2 год * 15°/год = 30°; 15 хв : 4 хв = 3,75° = 3° 45', а) 30° + 3° 45' = 33° 45'; 4) 30° сх. д. + 33° 45' = 66°45' сх. д. в) 1) 12 год - 5 год 30 хв = 6 год 30 хв;

6 год х 15°/год = 90°;

30 хв : 4 хв = 7,5° = 7° 30', а 90° + 7° 30' = 97° 30';

30° сх. д. - 97° 30' = 67° 30' зх. д.

Відповідь: якщо у м. Біла Церква 12 год, то місцевий час 15 год буде на меридіані 75° сх. д.; 14 год 15 хв - на 66° 45' сх. д.; 5 год 30хв - на 67° 30' зх. д.

Методичні вказівки. Для виконання завдання слід скористатися картою годинних поясів у географічному

атласі. Слід пам’ятати, що нумерація годинних поясів ведеться від 0 до 23 номера (всього 24) у напрямку із заходу на схід, починаючи від нульового меридіана. Нумерація годинних поясів є наскрізною для Східної і Західної півкуль (на відміну від географічної довготи).

Якщо пункти знаходяться в різних півкулях (східній та західній), слід врахувати лінію зміни дат.

Задача

Визначте різницю в часі між Кременчуком (33°25΄ сх. д.) та Москвою (37°35΄ сх. д.) 12.05.2012 р. з урахуванням декретного часу.

Методичні рекомендації. У Росії діє декретний час: у кожному годинному поясі час переведено на

одну годину вперед та скасовано перехід на зимовий час.

Приклад

Визначте час сходу, заходу сонця та тривалість дня, якщо горизонтальний кут сходу сонця становив 120°.  Кутова швидкість осьового обертання Землі дорівнює 15° за годину, така ж швидкість видимого руху сонця на небосхилі. Горизонтальний кут (тобто, азимут) сходу сонця дорівнює 120°. Азимут – це кут між напрямом на північ (там сонце перебуває під горизонтом у полуніч) та напрямом на світило. Відтак, сонце від полуночі пройшло під горизонтом 120°; тобто, цей шлях воно подолало за 8 годин (120°:15°). Точка заходу лежить симетрично щодо точки сходу, тобто, горизонтальний кут заходу сонця становить 240° (360° – 120°). У часі це буде: 240° : 15° = 16 годин. Залишається вирахувати тривалість дня: 16 год. – 8 год. = 8 год. Або ж можна розмірковувати так: якщо від полуночі до сходу сонця пройшло 8 годин, то й від заходу до полуночі також буде 8 годин. Тобто, сонце зайшло за горизонт о 16 годині (24 год. – 8 год.). Відповідь: сонце зійшло о 8 годині ранку, зайшло щ 16 годині, день тривав 8 годин.

Способи визначення масштабу топографічної карти

За кілометровою сіткою. На всіх топографічних картах друкується кілометрова сітка. Сторони квадратів сітки відпо­відають певній кількості кілометрів. Це можна легко визначити за підписами на вихідних лініях біля рамки карти. Припустимо, що відстань між двома сусідніми лініями дорівнює 1 км. Вимі­рюємо цю відстань лінійкою і у нас виходить 2 см. Це значить, що масштаб даної карти: в 1 см 500 м (1000 : 2) або 1 : 50 000.

За довжиною дуги меридіана. Пам'ятаємо, що одна мінута по меридіану на місцевості дорівнює 1,85 км.

Визначення масштабу глобуса і карти

Якщо потрібно визначити масштаб глобуса чи карти, то це можна зробити в тому випадку, коли відома відстань між двома об'єктами на місцевості. Знаючи відстань між ними на глобусі чи карті, складаємо відношення:

М - масштаб; L - відстань на місцевості і відстань на глобусі чи карті.

М = L (глобуса) : L ( місцевості )

Задача Визначте масштаб карти, якщо відстань на місцевості між Києвом і Тернополем становить 480 км, а на карті вона дорівнює 48 см.

Розв'язання: для того щоб визначити масштаб карти, потрібно скласти відношення відстані на карті до відстані на місцевості:

М = L (к) : L (м ) = 48 см : 480 км = 1см / 10 км

Ми отримати іменований масштаб в 1 см 10 км, який переведемо у числовий, тобто кілометри переводимо в сантиметри: 1 : 1 000 000.

Відповідь: масштаб карти 1 : 1 000 000.

Задача 60. Визначте масштаб глобуса, якщо відстань на ньому між екватором і 10-ю паралеллю становить 2,2 см.

Розв'язання: для того щоб визначити масштаб глобуса, потрібно скласти відношення, де чисельник - це відстань на глобусі між двома об'єктами, а знаменник - відстань між цими об'єктами на місцевості.

Визначаємо відстань між двома точками на місцевості. Потрібно 10° (10° - 0° = 10°) помножити на довжину дуги 1° меридіана, яка, як відомо, становить 111,1 км:

10° х 111,1 км = 1111 км;

складаємо відношення, оскільки відстань між двома точками на глобусі нам відома - 2,2 см:

М = L (г) : L (м ) = 2,2 см : 1111 км = 1см/500 км

Отриманий іменований масштаб глобуса переводимо у числовий: 1 : 50 000 000.

Відповідь: масштаб глобуса 1 : 50 000 000\

Задача На карті якого масштабу парк займає площу 1см', якщо на карті масштабу 1:10 000 він має площу 25 см²?

Розв'язання: якщо площа парку на одній карті у 25 разів більша, ніж на іншій, то масштаб другої карти є дрібнішим у 5 разів, тобто 1 : 50 000.

Відповідь: парк займає площу 1см" на карті масштабу 1: 50 000.

Задача 64. Яку площу займає Україна на карті півкуль, що має масштаб 1 : 22 000 000?

Розв'язання: в 1см цієї карти 220 км, в 1 см2 - 48 400 км2 (220x220); площа України 603 700 км2;

603 700 км² : 48 400 км²= 12,47 см².

Відповідь: на карті масштабу 1: 22 000 000 Україна займає площу 12.47 см2.

МАСШТАБ

Масштаб записують як частку, діленим якої є одиниця, а дільником — число, що вказує, у скільки разів реальні розміри більші, ніж розміри на карті чи плані.

Наприклад, якщо на плані задано масштаб 1 : 1000, то це означає, що 1 см на плані відповідає 1000 см на місцевості, що становить 10 м.

Швидке переведення з числового в іменований масштаб: відкидаємо 2 нулі – отримуємо метри (1:600=в 1см 6м), відкидаємо 5 нулів – отримуємо кілометри (1:2000000 = в 1с 20км).

Приклад

Маємо карту з масштабом 1 : 10 000 000, відстань між містами Київ і Харків дорівнює 4,5 см на карті. Яка відстань між містами Київ і Харків на місцевості?

Зрозуміло, що масштаб показує, що реальна відстань між містами більша від відповідної відстані на карті у 10 000 000 разів. Тому шукана відстань дорівнює 4,5 · 10 000 000 = 45 000 000 см = 450 км. Отже, відстань між Києвом і Харковом 450 км.

Таким чином, щоб знайти відстань між двома містами, якщо відома відстань між їх зображеннями на карті масштабом 1 : п, треба:

1) виміряти відстань між цими містами на карті;

2) помножити отриману відповідь на число.

Приклад

Який масштаб має карта, якщо відомо, що сад квадратної форми на ній займає площу в 4 рази меншу, ніж на карті масштабу 1:100 000. В 1 см 1 км. По суті, якщо площа менша в 4 рази, то лінія - у 2 рази. Можливо, тоді в 1 см 2 км, отже 1:200 000

Приклад

Площадь леса на плане с масштабом 1:100 000 имеет форму прямоугольника со сторонами 42 мм и 57 мм. Определите площадь леса в га.

Выразим стороны прямоугольника в масштабе плана:

1) а = 4,2 см * 100 000 = 420 000 см, т.е. 4200 м 2) b = 5,7 см * 100 000 = 570 000 см, т.е. 5700 м

В масштабе плана а = 4200 м, b = 5700 м.

3) S ABCD = 4200 м * 5700 м = 23 940 000 кв. м 1 га = 10 000 кв. м

4) 23 940 000 кв. м : 10 000 кв. м = 2394 га.

Ответ: Площадь леса равна 2394 га.

Приклад

Розрахуйте площу саду (у га), якщо на карті масштабу 1:50 000 він займає площу 2,4см². 2.4*500м*500м=60 га

Приклад

Визначте масштаб плану, якщо ліс площею 20 га охоплює на ньому 20 см кв.

На карті 20см²=20га 1см²=1га=10000м² Тобто 1 см = 100м

Масштаб в числовому вигляді 1:10000

Приклад

Визначте кількість дерев у лісі, який на плані масштабу 1:100 000 зображено прямокутником із сторонами 3 і 6 см і має такі буквенно-цифрові характеристики: сосна 12/0,2*3 Буквенно-цифрові характеристики лісів на топографічних картах сосна 12/0,2*3 означають: сосна – назва порід дерев, - позначення хвойних порід дерев, 12 – висота дерев у метрах, 0,20 – середня товщина дерев в метрах на відстані 1,3 метра від землі, 3 – відстань між деревами в метрах. Одному сантиметру на карті масштабу 1: 100 000 відповідає відрізок 1 км на місцевості. Розміри прямокутника на місцевості будуть становити 3 км і 6 км. Визначимо кількість дерев у кожній стороні прямокутника, знаючи середню відстань між ними:  3000 м : 3 = 1000 штук і 6000 м : 3 = 2000 штук Обчислимо кількість дерев за формулою: S = a*b=1000*2000 = 2 000 000 дерев

Приклад

Плодовый сад на плане 1 : 10 000 имеет форму прямоугольника со сторонами 97 мм и 63,5 мм. Определите площадь сада на местности. Решение: Масштаб – 1 : 10 000. В 1 см – 100м. 1) 9,7см х 6,35см = 61,595см² 2) 100м х 100м = 10 000 м² 1см2 = 10 000м²

3) 61,595см² х 10 000 = 615 950 м² 4) 1га = 10 000м² 5) 615 950м² : 10 000м²= 61,595 га Ответ: 61,595 га Приклад

Визначте, яку площу займає Україна на карті півкуль, яка не спотворює площу і має масштаб 1 : 22 000 000 А. 6,24 см. кв. Б. 25 см. кв. В. 12,47 см. кв. Г. 10,25 см. кв.

В настоящих цифрах площадь Украины равна 603700 км². У нас же масштаб в 1 см 220 км. Значит, 1 см² на карте - это 48400 км². А сколько же см² будет занимать Украина в 603700 км²? х = 603700/48400 = 12,47 см см². Ответ: В.

Приклад

Визначте масштаб глобуса, якщо Україна на ньому займає площу 6,7 см квадратних. Пояснення 1.Насправді площа України 603700 км2. На карті ж вона 6,7 см2. Тому маємо співвідношення 6,7 см2 = 603700 км² 1 см² = 90104,48 км² 1 см = корінь з 90104,48 км2= 300 км Тобто в 1см 300км = 1: 30 000 000 Відповідь: 1: 30 000 000

Пояснення 2.

1. Спочатку визначаємо, скільком км на місцевості відповідає 1 см на глобусі, масштаб якого нам потрібно визначити. для цього необхідно площу України (603 700 км) поділити на площу, яку вона займає на глобусі (6,7) 603 700 км : 6,7 = 90 104,5 км 2. Далі визначаємо іменований масштаб глобуса, тобто скільком кілометрам на місцевості відповідає 1 см на цьому глобусі. Якщо  1 см=90 104,5 км. отже, іменований масштаб глобуса в 1см 300 км. 3. далі переводимо іменований масштаб у числовий. масштаб глобуса 1 : 30 000 000. Відповідь: масштаб глобуса 1 : 30 000 000.

Визначення площ ділянок на планах місцевості й топографічних картах

Вимірювання площ за картою вимагає використання допоміжних прийомів. Одним з таких способів є геометричний. Суть цього способу полягає в тому, що території, площі яких потрібно визначити, розбивають на допоміжні фігури - трикут­ники, квадрати, трапеції, паралелограми і т. ін. Площу кожної фігури вираховують за відомими геометричними формулами. А сума окремих фігур дає загальну площу певної території.

Пропонуємо приклади задач, де використовуються геомет­ричні формули для визначення площ ділянок на плані чи карті.

Задача Визначте площу фруктового саду, якщо на плані масштабу 1 : 5 000 він має форму квадрата, діагональ якого на цьому плані дорівнює 12 см.

Розв'язання: площа квадрата (S) визначається за формулою:

S = а² = ½ d², де а - сторони квадрата, d - діагональ.

Визначаємо площу саду на плані: S= 1|2 х 12² = 72 см²; числовий масштаб карти: 1 см = 50 м;

визначаємо, чому дорівнює 1 см² на місцевості: см² = 50м х 50 м = 2 500 м²;

визначаємо площу саду на місцевості: 500 м² х 72 = 180 000 м²;

переводимо м² у га (1 га = 10 000 м²) 180 000 м²: 10 000 м² = 18га. Відповідь: площа саду 18 га.

Задача Визначте площу ріллі, якщо на плані масштабу 1 : 5 000 вона має форму прямокутного трикутника, один з катетів якого дорівнює 50 мм, а другий - 48 мм.

Розв'язання: площа прямокутного трикутника (S) визначається за формулою:

S =1|2 ab, де а,Ь - катети. Визначаємо площу ріллі на плані: S = 1|2 х 5см х 4,8 см = 12 см²; числовий масштаб карти: в 1 см - 50 м; визначаємо, чому дорівнює 1 см² на місцевості:

см² = 50 м х 50 м = 2 500 м²; визначаємо площу саду на місцевості: 500 м² х 12 = 30 000 м²;

переводимо м у га (1 га = 10 000 м²): 30 000 м2: 10 000 м2 = 3 га. Відповідь: площа ріллі 3 га.

Кілометрова сітка

На аркушах топографічних карт, як зазначалося раніше, нанесено кілометрову (прямокутну) сітку. Біля кожної лінії записані її координати. Так, надпис на першій горизонтальній лінії 6015 означає, що всі точки, які розташовані на цій лінії (лінії Y), знаходяться від екватора на відстані 6015 км.

А надпис 3435 біля вертикальної лінії (лінії X) означає: 3 - номер зони, а 435 - ординату лінії у кілометрах, розташовану на захід від осьового меридіана зони на 65 км (500км - 435 км = 65 км).

Якби дана вертикальна лінія позначалась тризначною цифрою, більшою за 500, то це означало б, що лінія знаходиться на схід від осьового меридіана.

Усі наступні лінії кілометрової сітки, за винятком останньої горизонтальної і останньої вертикальної, позначені лише двозначними числами. Це зроблено з метою, щоб не було повторень і перевантаження інформацією топографічної карти.

Визначення прямокутних координат точок за топографічною картою

Щоб визначити наближено місцеположення будь-якого географічного об'єкта або точки на карті, потрібно назвати утворений кілометровими лініями квадрат, у якому вони знаходяться. Для цього слід прочитати за рамкою двозначні числа, що позначені великими цифрами біля горизонтальної і вертикальної ліній, які утворюють нижній лівий (південно- західний) кут потрібного квадрата. Наприклад. 15-35. Першими пишуть цифри, що позначають горизонтальні лінії.

Для того щоб визначити прямокутні координати заданої точки, потрібно виміряти за перпендикулярами відстань від цієї точки до нижньої горизонтальної і лівої вертикальної ліній й отримані значення скласти з координатами ліній. Після вимірювання відстаней від ліній кілометрової сітки до певної точки записують їх координати. Наприклад, X = 15 560; Y = 35 450.

Записані в такому вигляді координати точки називаються неповними (скороченими). Вони показують, у якому кілометро­вому квадраті знаходиться дана точка і її відстань у метрах від кілометрових ліній. Так можна показати положення точки лише в межах однієї зони, адже аналогічні координати можуть мати й інші точки, що розташовані у різних зонах. Тому потрібно викорис­товувати повні координати. Для всіх точок, що розташовані в межах України, прямокутні координати записуються у вигляді семизначного числа. Для цього до зазначених вище значень координат X та Y попереду дописують ще по дві цифри. Ці цифри вказані малим шрифтом біля північної і південної горизонтальних та західної і східної вертикальних ліній кілометрової сітки. Наприклад, X = 6515 560; Y = 4335 450. У даному випадку перше число означає, що точка віддалена від екватора на 6515 км 560 м, а друге показує, що точка розташована у 4-й зоні і має координату в ній 335 км 450 м, тобто вона віддалена від осьового меридіана 4-ї зони у західному напрямку на 164 км 550 м (500 км - 335 км 450 м= 164 км 550 м).

Задача 94. Визначте масштаб топографічної карти, на якій відстань між точками А і В, які мають такі плоскі прямокутні координати: А (X = 6066325; Y = 4311500);

В (X = 6065825; Y = 4311500), становить 2 см.

(Відповідь: 1 : 25 000)

При встановленні компаса по лінії координатної (кіломет­рової, прямокутної) сітки враховують поправку напрямку як сумарну величину, яка включає в себе магнітне схилення і зближення меридіанів, а при встановленні компаса по боковій стороні рамки карти враховують тільки магнітне схилення.

Визначення напрямів за топографічною картою

Орієнтування на місцевості, а також вирішення багатьох спеціальних задач здійснюється через визначення азимутів, румбів і дирекційних кутів напрямків.

Орієнтувальні кути позначаються: дійсний азимут Ад, маг­нітний азимут Ам, дійсний румб Rд, магнітний румб RM. дирекційний кут а, дирекційний румб Rx.

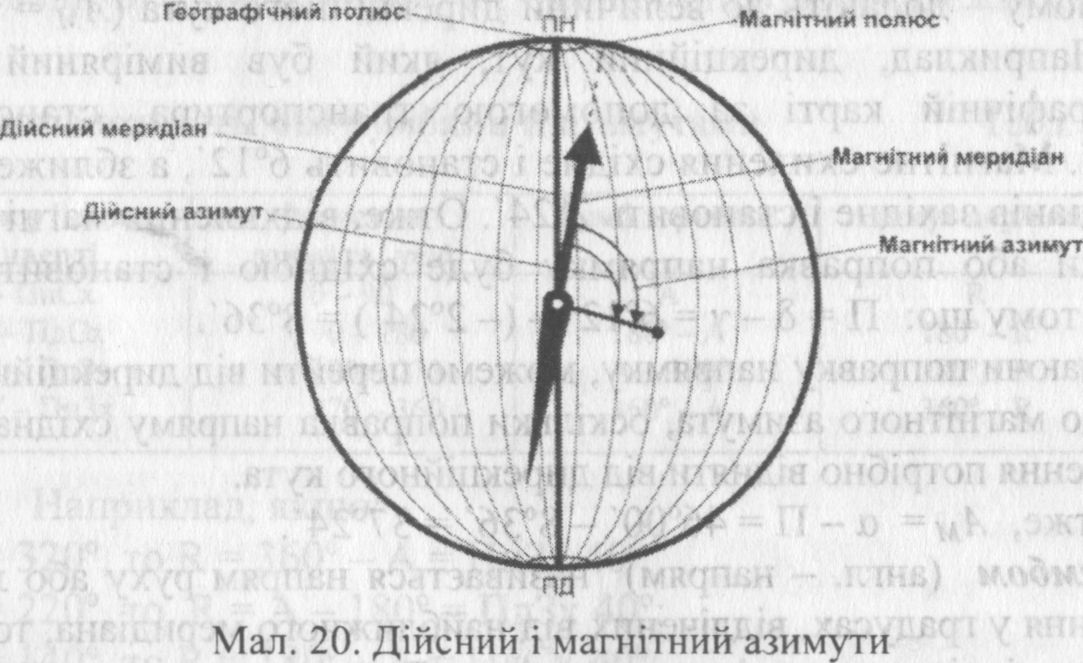
Азимут - це кут (напрям руху) у градусах між північним кінцем меридіана за ходом годинникової стрілки і заданою лінією. Азимути вимірюються від 0 до 360°. Вони називаються магнітними або дійсними залежно від того, який з меридіанів є початковим напрямом.

Розрізняють два види азимутів: дійсний (істинний) (Ад) і магнітний (Ам). '

Дійсним (істинним) азимутом (Ад) називається кут від 0" до 360°, що відрахований за ходом годинникової стрілки від північного напрямку географічного (істинного) меридіана до напрямку на місцевий предмет.

Магнітний азимут (Ам) - це кут від 0° до 360°, виміряний за ходом годинникової стрілки від північного напрямку магнітного меридіана до напрямку на місцевий предмет. Магнітний азимут визначається за допомогою магнітної стрілки .

Для того щоб перейти від дійсного азимута до магнітного, потрібно відняти величину східного схилення від величини дійсного азимута, або, якщо схилення західне, додати його до дійсного азимута/

Для переходу від дійсного азимута до азимута магнітного використовують формулу:

Ам= Ад± δ.

Задача 100. За допомогою транспортира на топографічній карті був виміряний дійсний азимут, він становив 56° ЗО' (Ад = 56° ЗО'), а магнітне схилення східне і дорівнює 6° 12' (5 = 6° 12'). Визначте магнітний азимут (Ам).

Розв'язання: Ам= Ад- 8 = 56° ЗО' - 6° 12' = 50° 18:

Відповідь: магнітний азимут становить 50° 18'.

Задача 101. Визначте магнітний азимут (Ам) на точку В, якщо дійсний азимут (Ад) становить 32° 18', а магнітне схилення (8), яке вказане на топографічній карті є східним і дорівнює 1° 48'. (Відповідь: 30° 30')

Дирекційний кут (ά) - це кут між північним напрямком вертикальної лінії координатної (кілометрової, прямокутної) сітки і заданим напрямком на місцевий предмет від 0° до 360°, виміряний за ходом годинникової стрілки. Дирекційний кут на території зони дорівнює алгебраїчній різниці дійсного азимута й кута зближення меридіанів: = Ад - (±у).

Для переходу від дирекційного кута до магнітного азимута потрібно враховувати поправку напрямку. Азимут магнітний визначають за формулою: Ам = ά ± П.

Звідси ά = Ам ± П.

Якщо північний напрям магнітної стрілки відхиляється на схід від вертикальної координатної (кілометрової) лінії, то відхилення вважається східним, а якщо стрілка відхиляється на захід, то західним. При східному відхиленні поправку напрямку віднімають від величини дирекційного кута (Ам = а - П), а при західному - додають до величини дирекційного кута (Ам = а + П). Наприклад, дирекційний кут, який був виміряний на топографічній карті за допомогою транспортира, становив 46°00'. Магнітне схилення східне і становить 6°12', а зближення меридіанів західне і становить 2°24'. Отже, відхилення магнітної стрілки або поправка напрямку буде східною і становитиме 8°36', тому що: П = 8 - у = 6°12' - (- 2°24 ) = 8°36'.

Знаючи поправку напрямку, можемо перейти від дирекційного кута до магнітного азимута, оскільки поправка напряму східна, то її значення потрібно відняти від дирекційного кута.

Отже, Ам= а - П = 46°00' - 8°36' = 37°24'.

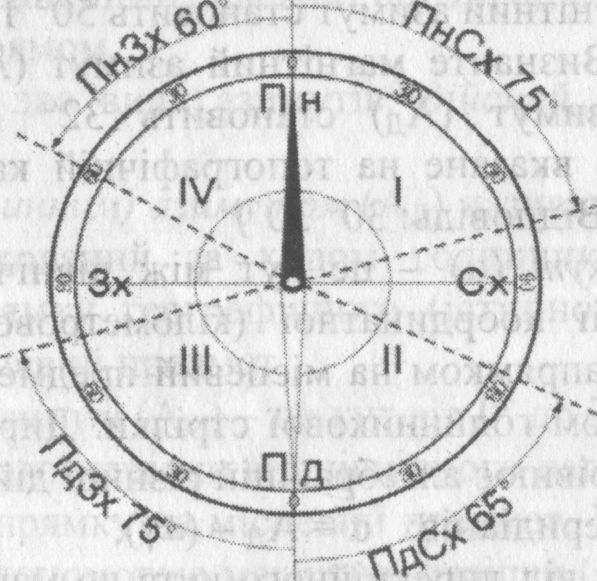
Румбом (англ. - напрям) називається напрям руху або лінії візування у градусах, відлічених від найближчого меридіана, тобто від його північного чи південного кінця. Для визначення румбів ви­діляють чотири чверті - по 90° у кожній (мал. 21) - і відлічують їх за годинниковою стрілкою від північного кінця меридіана. Вони називаються: перша (І) - Пн Сх (північно-східна); друга (II) - ПдСх (південно-східна); третя (III) - ПдЗх (південно-західна) і четверта (IV) - ПнЗх (північно-західна).

Мал. 21. Визначення румбів Градусна величина румбів напрямів може бути однаковою, тому перед нею ставлять назву чверті, наприклад: ПнСх 40°, ПдЗх 40°.

Залежно від того, який меридіан є початковим напрямом, румби бувають дійсними або магнітними, а якщо їх відлічують від осьового меридіана зони, то вони називаються дирекційними або осьовими. Румби й азимути - величини взаємозалежні (табл.

9).

Взаємозалежність між румбами й азимутами Табл. 9

Номер і назва чверті	Значення азимута, град	Румб дорівнює	Азимут дорівнює
І - ПнСх	0-90	А	R
II - ПдСх	90-180	180°-А	180° -R
III-ПдЗх	180-270	А - 180°	180"+ R
IV - ПнЗх	270 - 360	360° - А	360° - R

Наприклад, якщо:

А = 320°, то R = 360° - А = ПнЗх 40°;

А = 220°, то R = А - 180° = ПдЗх 40°;

А = 140°, то R = 180° - А = ПдСх 40°;

А = 40°, то R = А = ПнСх 40°.

А = 40°, то R = ПнСх 40°;

А = 140°, то R = ПдСх 40°;

А = 220°, то R = ПдЗх 40°;

А = 320°, то R = ПнЗх 40°.

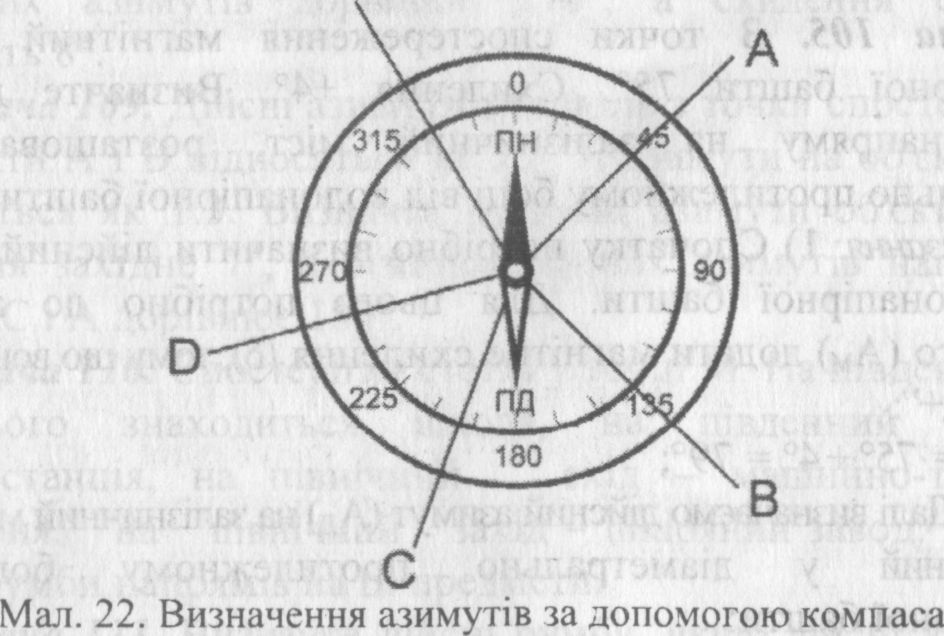
Задача 102. Використовуючи мал. 22, визначте азимути на предмети, що позначені буквами А, В, С, D, Б. Дані азимути переведіть у румби.

Задача 105. З точки спостереження магнітний азимут водонапірної башти 75°. Схилення +4°. Визначте дійсний азимут напряму на залізничний міст, розташований у діаметрально протилежному боці від водонапірної башти.

Розв'язання: 1) Спочатку потрібно визначити дійсний азимут (Ад) водонапірної башти. Для цього потрібно до азимута магнітного (Ам) додати магнітне схилення (8), тому що воно східне із знаком „+":

Ад= 75°+ 4° = 79°;

2) Далі визначаємо дійсний азимут (Ад) на залізничний міст, який розташований у діаметрально протилежному боці від водонапірної башти:

Ад=79°+180° = 259о.

Відповідь: дійсний азимут на залізничний міст становить 259°.

Задача 106. Дійсний азимут напряму з точки спостереження на вітряний двигун, що качає воду, дорівнює 30°. Схилення західне, 5°. Визначте магнітний азимут напряму на склади з пальним, що розміщені на відстані 25° на південь від вітряного двигуна.

Розв язання: 1. Визначаємо магнітний азимут (Ам) на вітряний двигун. Оскільки тут магнітне схилення західне, то воно береться із знаком „-".

Ад = Ам - 5, звідси Ам = Ад + 6 = 30° + 5° = 35°;

2. Далі визначаємо азимут магнітний (Ам) на склади з пальним. З умови задачі відомо, що вони розташовані на відстані 25° на південь від вітряного двигуна, тому:

Ам - 35° + 25° = 60°.

Відповідь: магнітний азимут на вітряний двигун становить 60°.

Висота Сонця над горизонтом

залежить від географічної широти місцевості. Із збільшенням географічної широти місцевості полуденна (максимальна) висота Сонця зменшується. Висота Сонця над горизонтом залежить і від пори року та часу доби. Наприклад, у залежності від пори року на екваторі вона може змінюватися від 90° до 66° 30'; на 45° пн. ш. від 68° 30' до 21° 30', а на Північному полюсі від 23° 30' до 0°.

У дні весняного й осіннього рівнодення (21 березня і 23 вересня), коли Сонце знаходиться в зеніті над екватором, полуденну висоту Сонця вираховують за формулою: h = 90° - φ,

де h - кут, під яким знаходиться Сонце над горизонтом опівдні, а φ- географічна широта місця спостереження. У Києві вона буде становити: 90° - 50°30' = 39°30'; на екваторі: 90°- 0° = 90°; на полюсах: 90°- 90° = 0°

У інші дні полуденна висота визначається за формулою: h = 90° - φ ± 5, де δ - схилення Сонця.

Влітку (22 червня), коли Сонце знаходиться в зеніті над Північним тропіком (тропіком Рака), полуденна висота його для північної півкулі збільшується на 23° 27', оскільки географічна широта Північного тропіка становить 23° 27'пн. ш., тобто = + 23° 27', звідси h = 90° - φ + δ, і для Києва вона становитиме:

h = 90° - 50° ЗО'+ 23° 27';

h = 62° 57' (це максимальна висота Сонця над горизонтом для м.Києва).

А взимку (22 трудня), коли Сонце знаходиться в зеніті над Південним тропіком, 23° 27' пд. ш., (тропіком Козерога), полу­денна висота його для північної півкулі зменшується на 23° 27', тобто δ = - 23° 27', і для Києва вона становитиме:

h = 90° - 50° 30'- 23° 27';

h = 16° 03' (це мінімальна висота Сонця над горизонтом для м.Києва).

В усі інші дні потрібно знати, на скільки і в бік якої півкулі схилилось Сонце, тобто над якою широтою воно в зеніті опівдні.

Задача Київ і Одеса розташовані майже на одному меридіані. 22 червня опівдні висота Сонця над горизонтом у Києві становить 63°, а в цей момент в Одесі - 67°. Визначте географічну широту цих міст і відстань між ними в градусах і кілометрах.

Розв'язання: 1) Використовуючи формулу визначення полу­денної висоти Сонця над горизонтом для літнього періоду h = 90° - φ ± δ, визначаємо географічну широту Києва, де φ = 90° - h ± δ, звідси:

φ = 90° - 63° + 23°27';

φ = 50°27' пн. ш.;

За таким же принципом визначаємо географічну широту Одеси:

φ = 90° - 67° + 23° 27';

φ = 46°27' пн. ш.;

Далі визначаємо відстань між цими містами у градусах:

50°27' - 46°27' = 4°;

Знаючи, що довжина дуги 1° меридіана становить приблизно 111,1 км, визначаємо відстань між даними містами:

4° х 111,1 км = 444,4 км.

Відповідь: географічна широта Києва 50°27' пн. ш., Одеси - 46°27' пн. ш„ відстань між ними 4°, або 444,4 км.

Задача 117. Висота полуденного Сонця над горизонтом у населеному пункті дорівнює 51° 20'. У цей же день опівдні Сонце в зеніті буває на 10° 30' пн. ш. Визначте географічну широту населеного пункту.

Розв'язання: 1) За формулою φ= 90° - h ± δ визначаємо географічну широту населеного пункту:

51° 20'- 90 0 - ф + 10° 30';

φ = 90°-51° 20' + 10° 30 ';

φ= 49° 10' пн. ш.

Відповідь: географічна широта населеного пункту становить 49° 10' пн. ш.

Задача 118. Полуденна висота Сонця над горизонтом у пункті А, який розташований у північній півкулі, 1 січня становить 36° 53'. Чи може Сонце в цьому пункті знаходитись в зеніті, якщо 1 січня δ = -23° 07'?

Розв 'язання: 1) За формулою φ = 90° - h ± δ визначаємо географічну широту населеного пункту:

36° 53'= 90° - φ - 23° 07';

звідси φ = 90° - 36° 53'- 23° 07';

φ = 30° пн. ш.

Відповідь: Сонце не може знаходитися в цьому пункті у зеніті, бо пункт А розташований на 30° пн. ш., тобто за межами тропіків.

Задача 119. Визначте, чи може Сонце знаходитись у зеніті в пункті, якщо в день весняного рівнодення полуденна висота його дорівнює тут 70°?

Розв'язання: 1) Оскільки в день весняного рівнодення (21 бе­резня) Сонце знаходиться в зеніті над екватором, то δ = 0°.

Звідси: h = 90°-φ;

70° = 90° - φ;

φ = 90° - 70°;

φ =0°.

Відповідь: Сонце може знаходитися в цьому пункті в зеніті, бо даний пункт розташований на 20-ій паралелі.

Задача 120. На екваторі опівдні 23 вересня вертикально поставлена рейка не відкидає тіні. У цей самий час тінь від рейки, вертикально поставленої в пункті А, що знаходиться в південній півкулі, дорівнює довжині рейки. На якій широті знаходиться пункт?

Розв язання.1) Якщо довжина тіні від рейки і самої рейки однакові, то кут становитиме 45°, а оскільки це день осіннього рівнодення, то Сонце опівдні знаходиться в зеніті над екватором, звідси 8 = 0°. За формулою h = 90° - φ визначаємо географічну широту точки А. Вона становитиме:

φ = 90° - 45°;

φ = 45°.

Пункт знаходиться у південній півкулі, тому широта буде південна.

Відповідь: пункт знаходиться на широті - 45° пд. ш.

Задача 121. Визначте максимальну висоту Сонця над горизонтом на Південному полярному колі опівдні 21 березня, 23 вересня, 22 червня, 22 грудня.

Розв'язання: 1) Використовуючи формулу h = 90° - φ ± δ, визначаємо максимальну висоту Сонця над горизонтом на Південному полярному колі опівдні 21 березня і 23 вересня. Оскільки це дні весняного й осіннього рівнодення, то δ = 0°, а географічна широта Південного полярного кола становить 66° 30' пд. ш. Звідси: h = 90°- 66° 30'; h = 23° 30'.

2) Далі визначаємо висоту Сонця над горизонтом на Південному полярному колі опівдні 22 червня та 22 грудня. 22 червня для південної півкулі δ = - 23° 30'. Звідси: h = 90° - 66° 30' - 23° ЗО': h = 0° 22 грудня для південної півкулі δ= + 23° 30'. Звідси: h = 90° - 66° 30' + 23° 30 і h = 47°.

Відповідь: максимальна висота Сонця над горизонтом на Південному полярному колі опівдні 21 березня і 23 вересня становить 23° 30', 22 червня - 0°, а 22 грудня - 47°.

Задача 123. Визначте географічну широту та відстань між двома населеними пунктами, якщо вони знаходяться в північній півкулі на одному меридіані, а висота полуденного Сонця 21 бе­резня у пункті А становить 39° 30', а в пункті В - 66° 30'.

Розв 'язання: 1) Оскільки в день весняного рівнодення (21 березня) Сонце знаходиться в зеніті над екватором, то 5 = 0°; використовуючи формулу h = 90° - ф ± б, визначаємо географічну широту пункту А:

φ = 90° - h ± δ;

φ = 90° - 39° 30';

φ = 50° 30' пн.ш. (широта міста Києва).

Аналогічно визначаємо географічну широту пункту В: φ = 90° -66° 30';

φ = 23° ЗО' пн.ш.(широта Північного тропіка).

Визначаємо відстань між цими пунктами у градусах і кілометрах:

50° 30'-23° 30'= 27°; 27° х 111,1 =2999,7 км.

Відповідь: географічна широта пунктів 50° 30' пн. ш. і 23° 30' пн. ш., а відстань між ними - 2999,7 км.

СОНЦЕ