Определитель n-го порядка и его свойства

Пусть дана прямоугольная таблица размером , которая называется матрицей.

– элемент матрицы, расположенный в -й строке и -м столбце.

Определение 3.7: Определителем матрицы называется алгебраическая сумма слагаемых, составленная следующим образом: слагаемыми являются всевозможные произведения из элементов матрицы , взятых по одному из каждой строки и из каждого столбца матрицы, причем слагаемое берется со знаком плюс, если его индексы составляют четную подстановку, и со знаком минус – в противном случае.

Подстановка получается следующим образом: всякое слагаемое определителя имеет вид: и определяет подстановку , о четности которой и говорится в определении.

Определитель матрицы обозначается одним из следующих способов: .

В частности: ,

Определение 3.8: Матрица 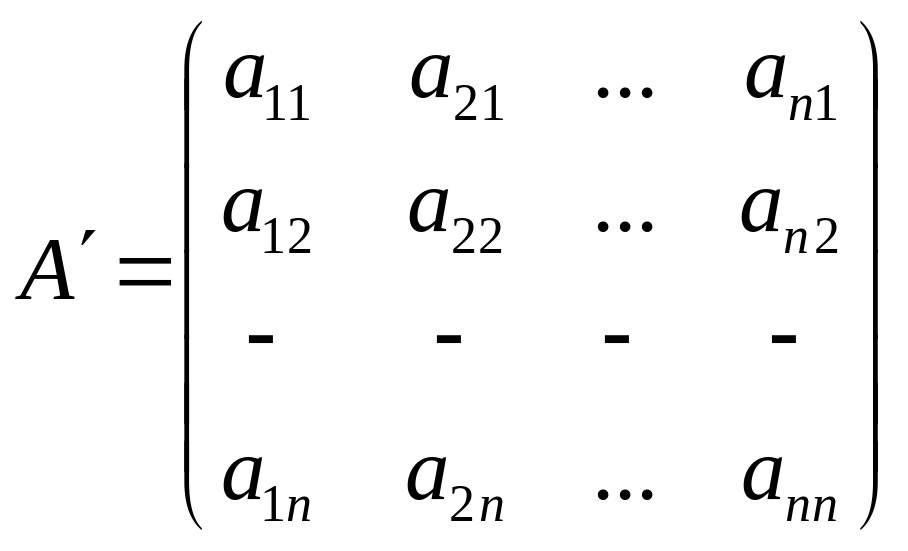называется транспонированной матрицей по отношению к матрице .

У матрицы столбцами являются строки матрицы , а строками – столбцы матрицы .

Если , то .

Свойства определителя

1. .

Замечание: Строки и столбцы матрицы определителя будем называть строками и столбцами определителя.

2. Строки и столбцы определителя равноправны, то есть если доказано какое-либо утверждение относительно строк определителя, то оно будет выполняться и для столбцов определителя.

3. Если некоторая строка определителя состоит только из нулей, то определитель равен нулю.

4. От перестановки двух строк определитель меняет знак.

5. Определитель, содержащий две одинаковые строки, равен нулю.

6. Если все элементы некоторой строки определителя умножить на некоторое число , то сам определитель умножится на .

7. Определитель, содержащий две пропорциональные строки, равен нулю.

8. , где .

Пусть даны две строки: , .

Введем операции над строками: , и если – число, то .

Определение 3.9: Строка является линейной комбинацией строк , если существуют числа такие, что .

9. Если одна из строк определителя есть линейная комбинация его других строк, то определитель равен нулю.

10. Определитель не изменится, если к элементам одной из его строк прибавляются соответственные элементы другой строки, умноженные на некоторое число.

11. Если к элементам некоторой строки определителя прибавить линейную комбинацию других строк определителя, то определитель не изменится.

Миноры и их алгебраические дополнения

Определение 3.10: Пусть дан определитель матрицы -го порядка. Выделим в нем строк ( ) и столбцов. Элементы матрицы , расположенные на пересечении выделенных строк и столбцов, образуют определитель -го порядка, который называется минором данного определителя и обозначается .

Замечание: Элементы матрицы являются минором 1-го порядка.

Обозначим номера выделенных строк через , а столбцов – .

Определение 3.11: После вычеркивания выделенных строк и столбцов из матрицы остается определитель порядка , который называется дополнительным минором к минору .

Определение 3.12: Обозначим называется алгебраическим дополнением к минору .

В частности, обозначим через дополнительный минор к минору , а алгебраическое дополнение – .

Теорема 3.5: Произведение любого минора на его алгебраическое дополнение в определителе является алгебраической суммой, слагаемые которой будут слагаемыми данного определителя, причем они взяты с теми же знаками, с которыми они входят в .