Линейная алгебра и аналитическая геометрия
1.1. Матрицы и действия с ними.
1.2. Определители n-го порядка и их свойства. Разложение определителя по строке (столбцу). Решение систем n линейных алгебраических уравнений с n неизвестными по правилу Кремера.
1.3. Обратная матрица. Решение матричных уравнений с помощью обратной матрицы.
1.4. Системы линейных уравнений. Совместимость систем линейных алгебраических уравнений. Однородная и неоднородная системы. Решение системы линейных алгебраических уравнений методом Гаусса.
1.5. Ранг матрицы. Теорема Кронекера-Капелли. Вычисление ранга матрицы
1.6. Векторы на плоскости и в пространстве. Линейные операции над векторами. Линейно независимая система векторов. Размерность и базис векторного пространства. Проекция вектора на ось. Направляющие косинусы и длина вектора. Ортонормированный базис. Разложение вектора по базису.
1.7. Декартова система координат. Координаты точки. Расстояние между точками. Деление отрезка в заданном отношении.
1.8. Скалярное произведение векторов и его свойства. Координатное выражение скалярного произведения. Угол между векторами. Векторное и смешанное произведение векторов, их основные свойства и геометрический смысл. Координатное выражение векторного и смешанного произведения.
1.9. Уравнения прямой на плоскости. Различные формы уравнений прямой на плоскости. Угол между прямыми. Расстояние от точки до прямой.
1.10. Прямая и плоскость в пространстве. Уравнение плоскости и прямой в пространстве. Угол между плоскостями. Угол между прямыми. Угол между прямой и плоскостью.
1.11. Кривые второго порядка: эллипс, гипербола, парабола. Их геометрические свойства и уравнения. Полярные координаты на плоскости.
1.12. Уравнения поверхности в пространстве.
1.13. Линейные пространства. Линейная зависимость и независимость системы векторов. Размерность и базис линейного пространства. Координаты вектора. Преобразование координат при переходе к новому базису.
1.14. Собственные значения и собственные векторы линейного оператора. Характеристический многочлен.
1.15. Билинейные и квадратичные формы. Матрица квадратичной формы. Приведение квадратичной формы к каноническому виду. Формулировка закона инерции. Критерий Сильвестра положительной определенности квадратичной формы.
Контрольная работа №1
СЕМЕСТР 2
Вариант 1
1.
Перемножить матрицы:
.
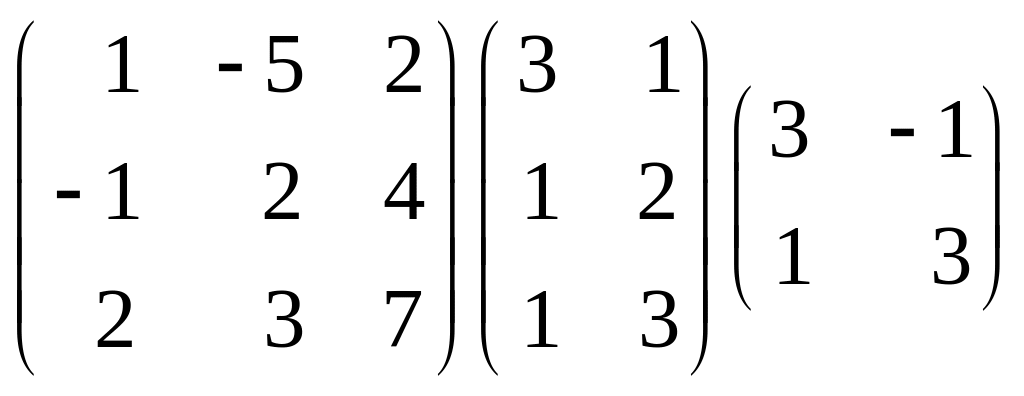2.
Вычислить определители: а)
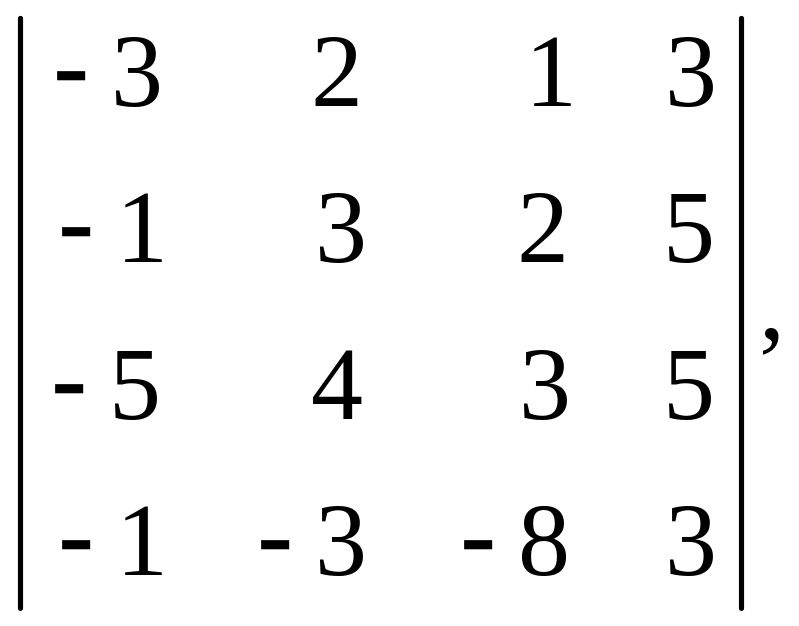б)
.
3. Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.
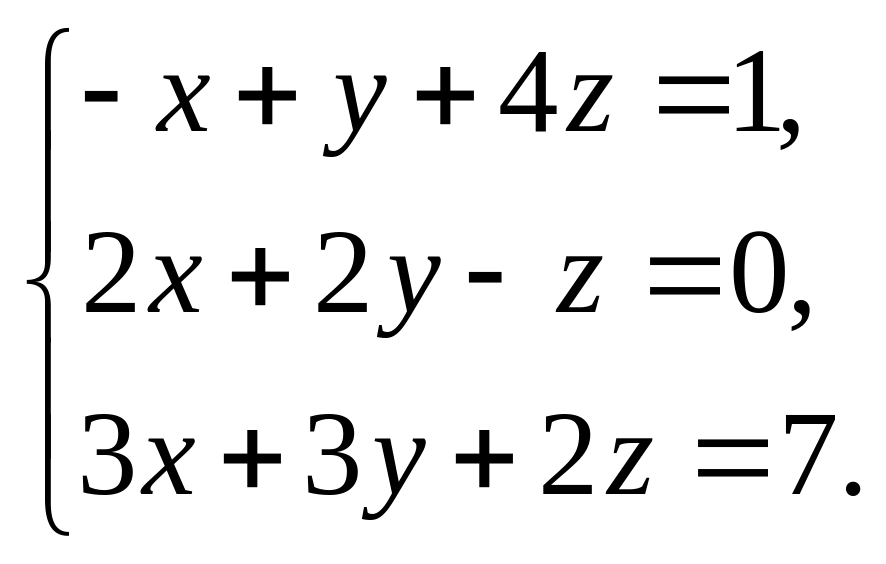
4. Найти общее решение методом Гаусса
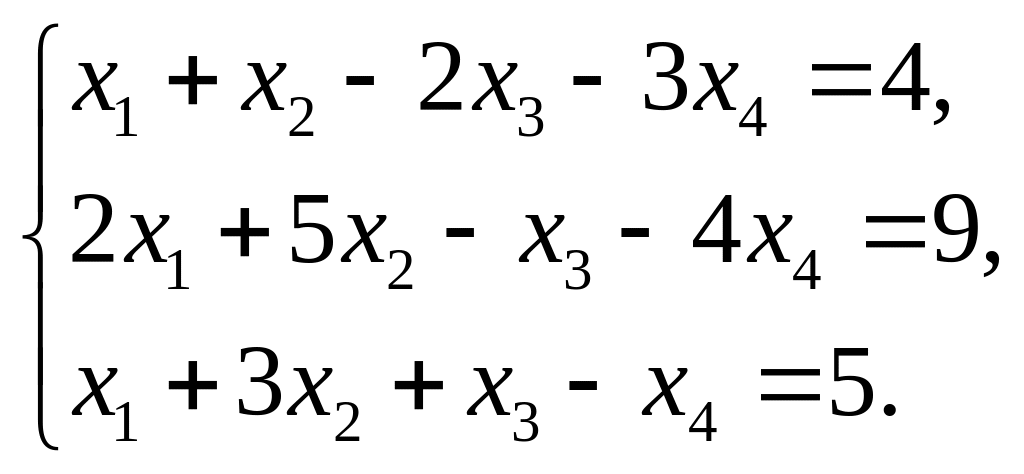
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:
.
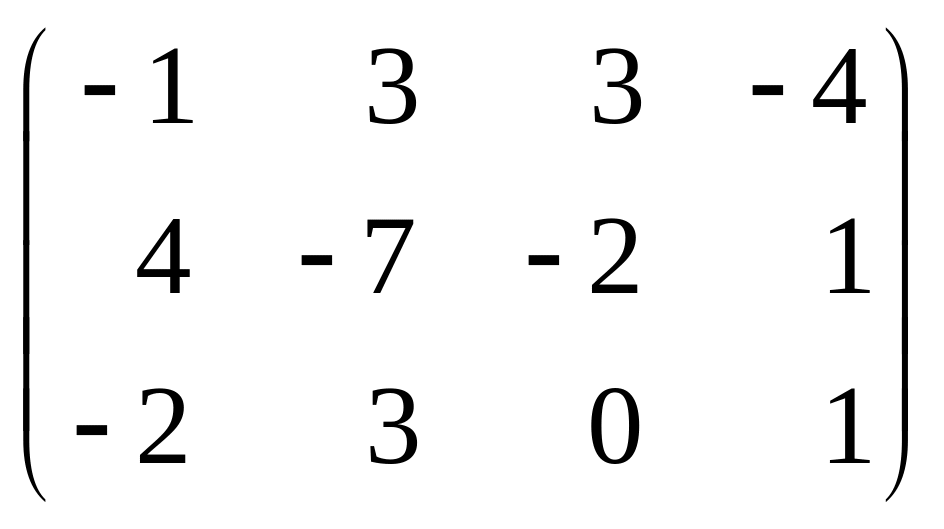6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (2;–1;1), b = (–1;2;1), c = (1;3;1), d = (–1;–2;3).
7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:
а) (2a–b)(3a+4b), б) |(2a–b)(3a+4b)|,
где |a|=2, |b|=3, a^b=/6.
8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(1;3;3), B(–1;2;–2), C(0;–1;3), D(2;1;0).
9. Составить уравнение плоскости, проходящей через две параллельные прямые:
и
.
10. Построить кривую = 2sin(2), заданную в полярных координатах.
11. Вывести уравнение кривой, если сумма расстояний от каждой ее точки до точек F1(–5;0) и F2(3;0) есть величина постоянная и равна p=10. Сделать чертеж.
12. Привести уравнение 16x2–9y2–64x–54y–161=0 к каноническому виду, определить тип кривой и сделать чертеж.
Вариант 2
1.
Перемножить матрицы:
.
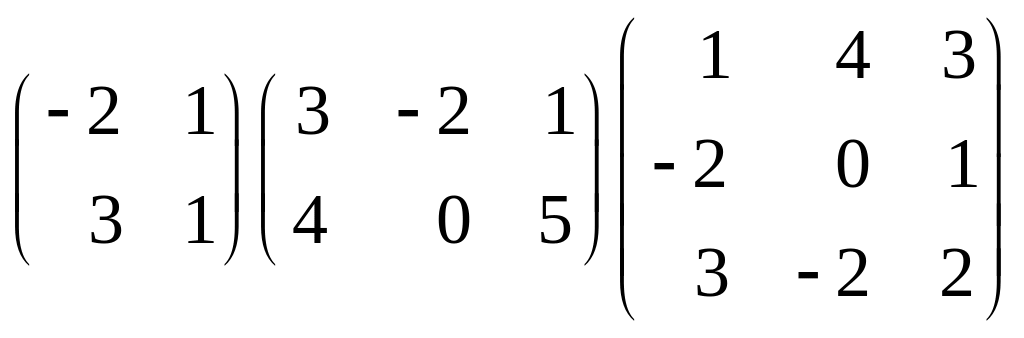2.
Вычислить определители: а)
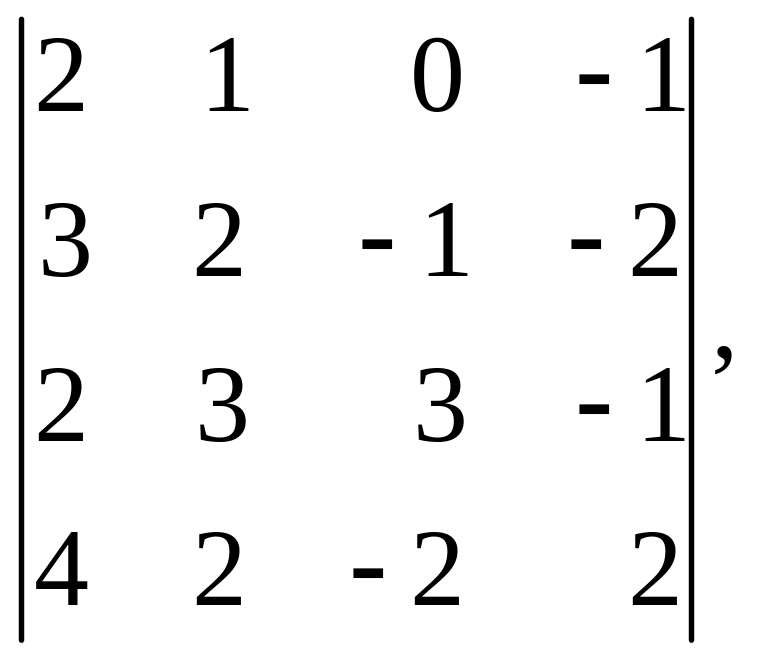б)
.
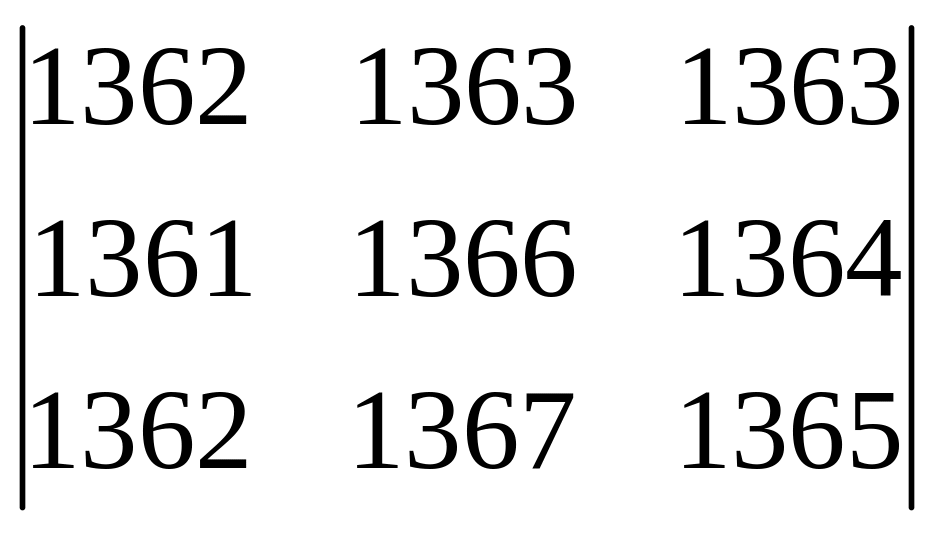3. Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.
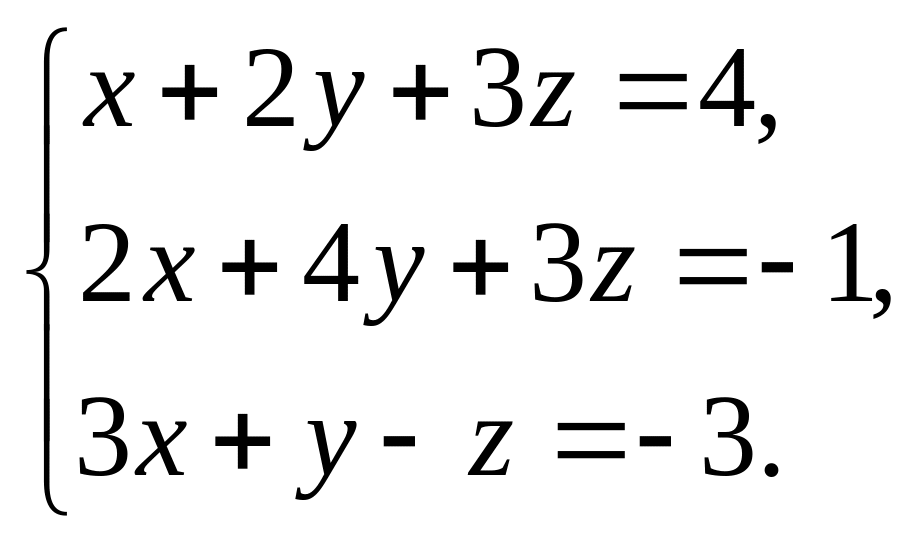
4. Найти общее решение методом Гаусса
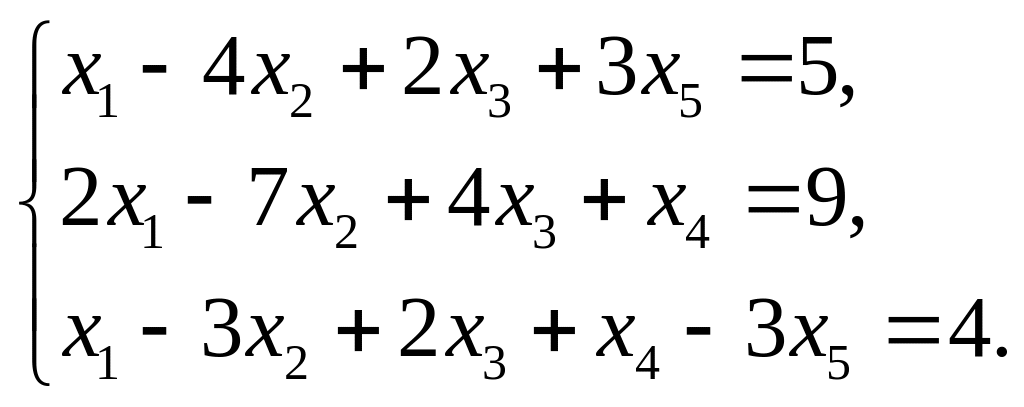
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:
.
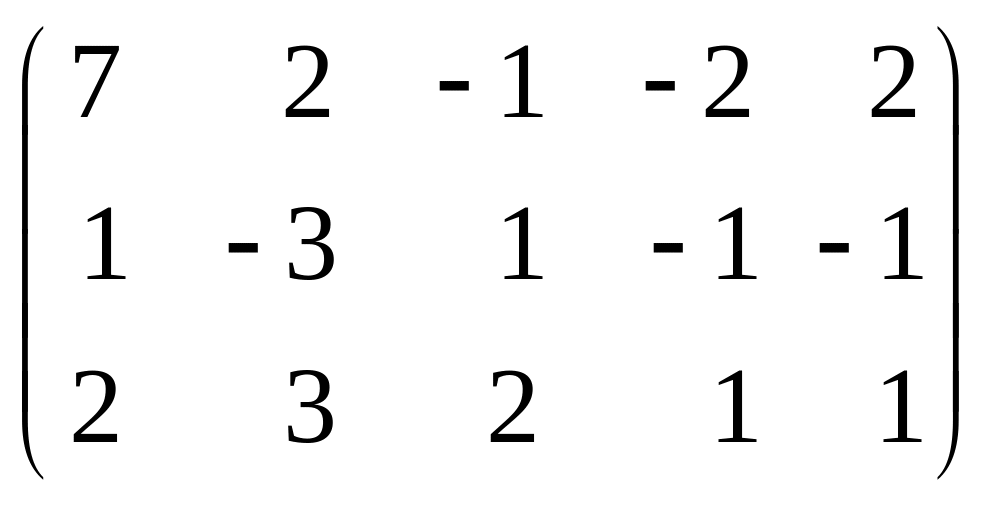6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (2;4;2), b = (–1;–2;–2), c = (3;5;1), d = (3;5;–1).
7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:
а) (a–3b)(2a+b), б) |(a–3b)(2a+b)|,
где |a|=4, |b|=2, a^b=2/3.
8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(3;2;1), B(1;–2;3), C(0;–1;4), D(2;1;0).
9. Составить каноническое уравнение прямой:
10. Построить кривую = 2(1+sin), заданную в полярных координатах.
11. Вывести уравнение кривой, если абсолютная величина разности расстояний от каждой ее точки до точек F1(–3;0) и F2(7;0) есть величина постоянная и равна p=6. Сделать чертеж.
12. Привести уравнение 4x2+5y2+24x+30y+61=0 к каноническому виду, определить тип кривой и сделать чертеж.
Вариант 3
1.
Перемножить матрицы:
.
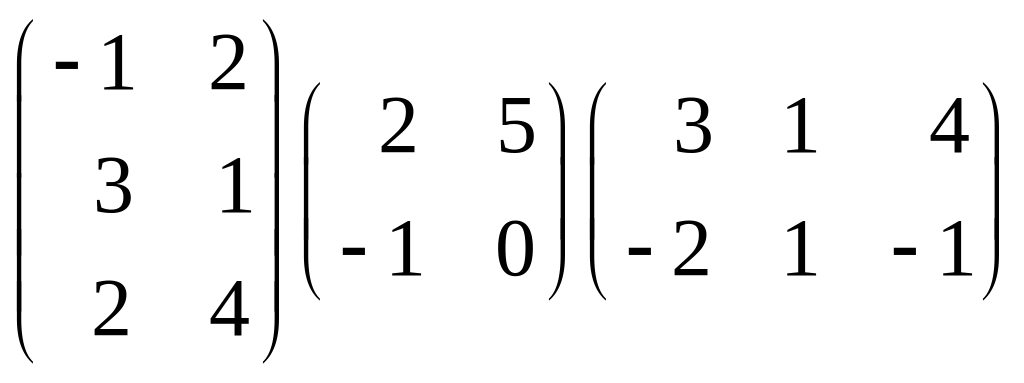2.
Вычислить определители: а)
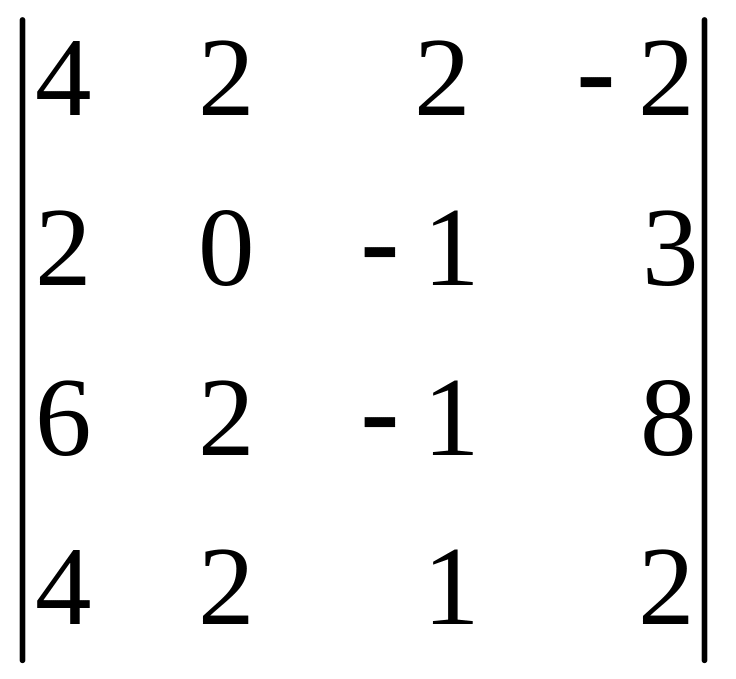б)
.
3. Решить систему линейных уравнений: а) методом Крамера, б) при помощи обратной матрицы, в) методом Гаусса.
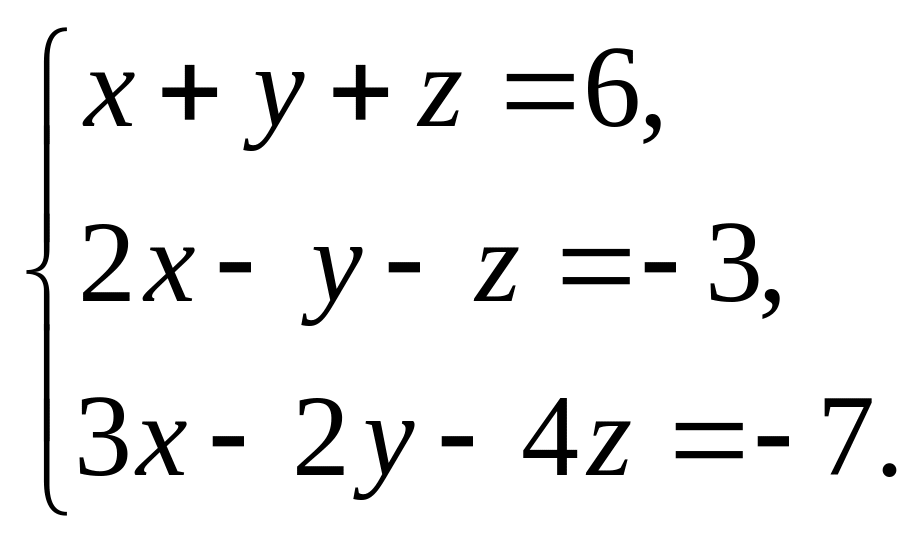
4. Найти общее решение методом Гаусса
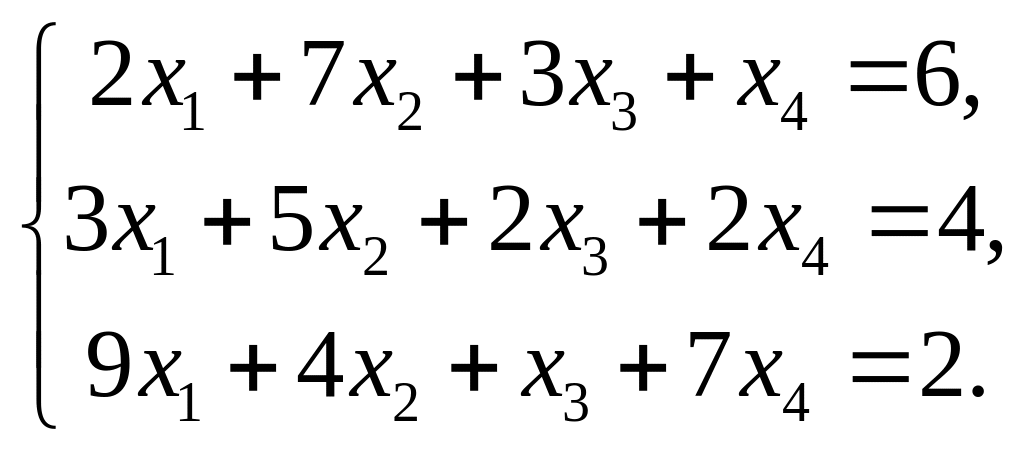
5. Вычислить ранг матрицы: а) методом окаймляющих миноров; б) методом элементарных преобразований:
.
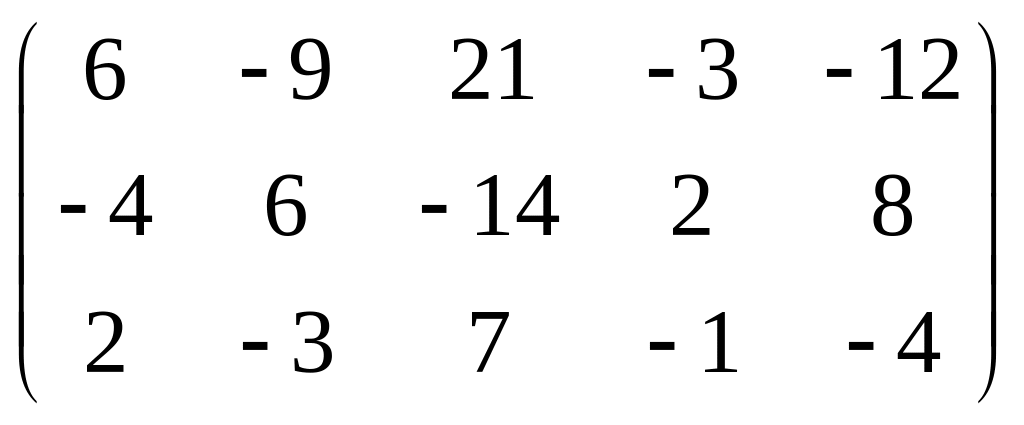6. Показать, что векторы a, b, c, образуют базис. Найти разложение вектора d по этому базису, если a = (2;2;3), b = (5;1;2), c = (–1;–3;–2), d = (8;0;1).
7. Вычислить выражения, используя определения и свойства скалярного и векторного произведений:
а) (a+2b)(b–3a), б) |(a+2b)(b–3a)|,
где |a|=2, |b|=3, a^b=/4.
8. Даны координаты вершин пирамиды ABCD. Найти: а) объем пирамиды, б) площадь грани ABC, в) косинус угла между ребрами AB и AC, г) уравнение прямой АВ, д) уравнение плоскости АВС, если A(2;–1;1), B(5;5;4), C(3;2;–1), D(4;1;3).
9. Составить уравнение плоскости, проходящей через две параллельные прямые:
и
.
10. Построить кривую = 2(1+sin), заданную в полярных координатах.
11. Вывести уравнение кривой, если сумма расстояний от каждой ее точки до точек F1(–4;0) и F2(2;0) есть величина постоянная и равна p=10. Сделать чертеж.
12. Привести уравнение 5x2–3y2–10x–18y–37=0 к каноническому виду, определить тип кривой и сделать чертеж.