
- •1. Линейная алгебра
- •1.1. Определения
- •1.2. Действия над матрицами
- •1.3. Определители
- •1.4. Обратная матрица
- •1.5. Системы линейных алгебраических уравнений
- •1.6. Системы (n) линейных уравнений с (n) неизвестными. Формулы Крамера
- •Матричный способ решения систем
- •1.8. Метод Гаусса
- •Задачи для контрольных заданий
- •Вариант 23
- •Список литературы
Задачи для контрольных заданий
Задачи 1–10. Показать, что система линейных уравнений имеет единственное решение, и найти его двумя способами: а) по правилу Крамера; б) матричным способом.
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
Задачи 11–20. Пользуясь методом Гаусса, найти общее решение системы линейных уравнений, а также два частных ее решения, одно из которых базисное.
11.
![]() 12.
12.
![]()
13.
![]() 14.
14.
![]()
15.
![]() 16.
16.
![]()
17.
![]() 18.
18.
![]()
19.
![]() 20.
20.
![]()
Задание 1
Решить матричное уравнение относительно неизвестной матрицы Х, если матрицы А, В, С, D, Е имеют вид:
 ,
,
![]() ,
,
 ,
,
![]() ,
,
 .
.
(символом Т обозначена транспонированная матрица)
АВ+2С=ЕХ, 6. СВТ=2А-Х,
D2-3ВА=2Х, 7. (АВ)Т+С=3Х,
(ВА)2=2DТ-Х, 8. 3DАТ=В+2Х,
СА-3ВТ=2Х, 9. АDТ+3ВТ=2Х,
DТВ=2АТ+2Х, 10. (АВ)2+Х=СВ-Е.
Задание 2.
Доказать совместность системы трех линейных уравнений с тремя неизвестными. Решить систему двумя способами: а) по формулам Крамера, б) методом последовательного исключения неизвестных (Гаусса).
1.
 2.
2.
 3.
3.

4.
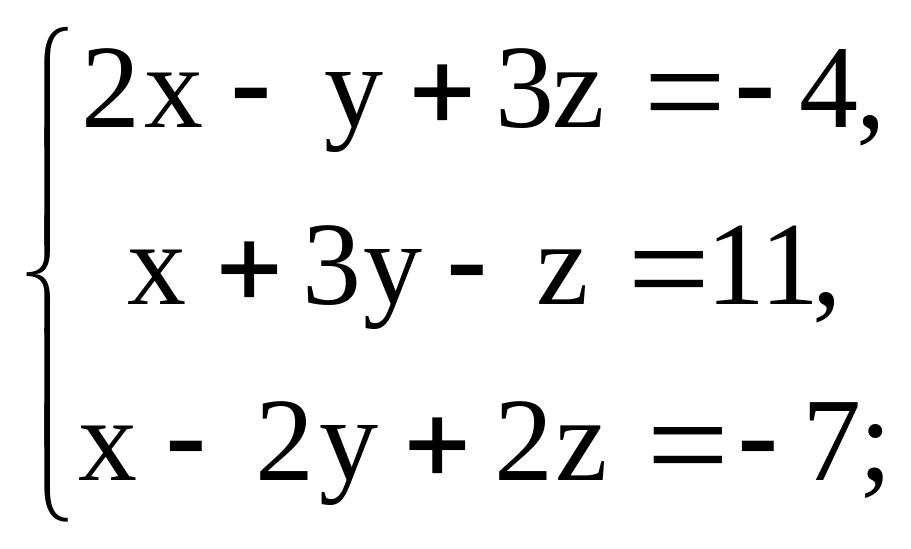 5.
6.
5.
6.
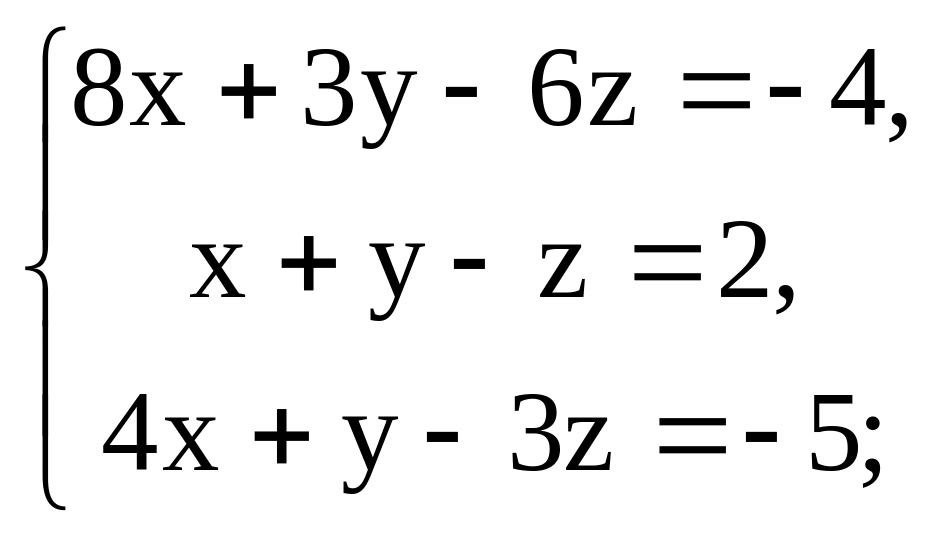
7.
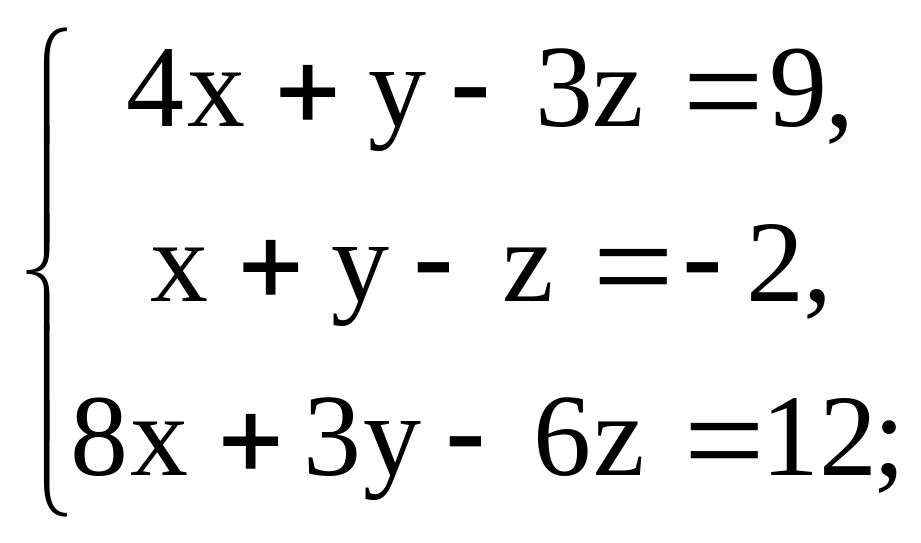 8.
8.
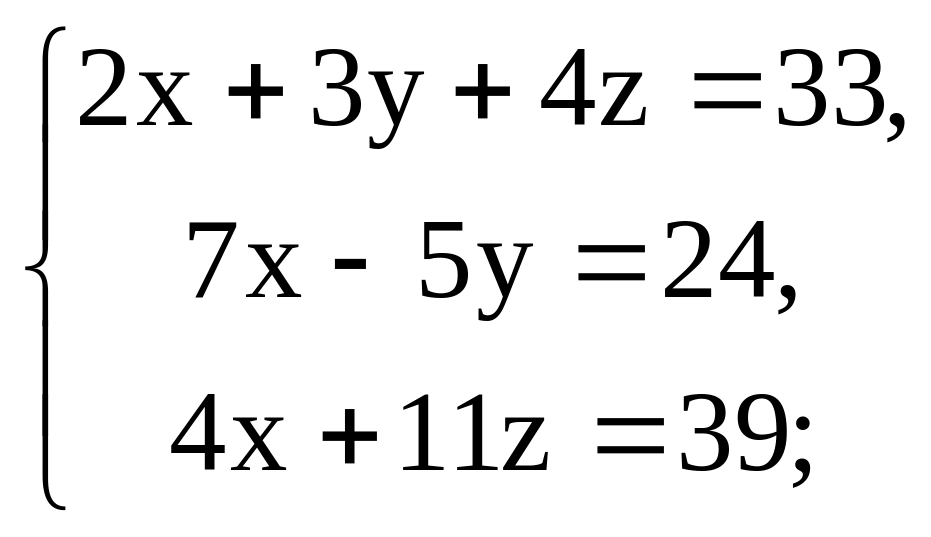 9.
9.
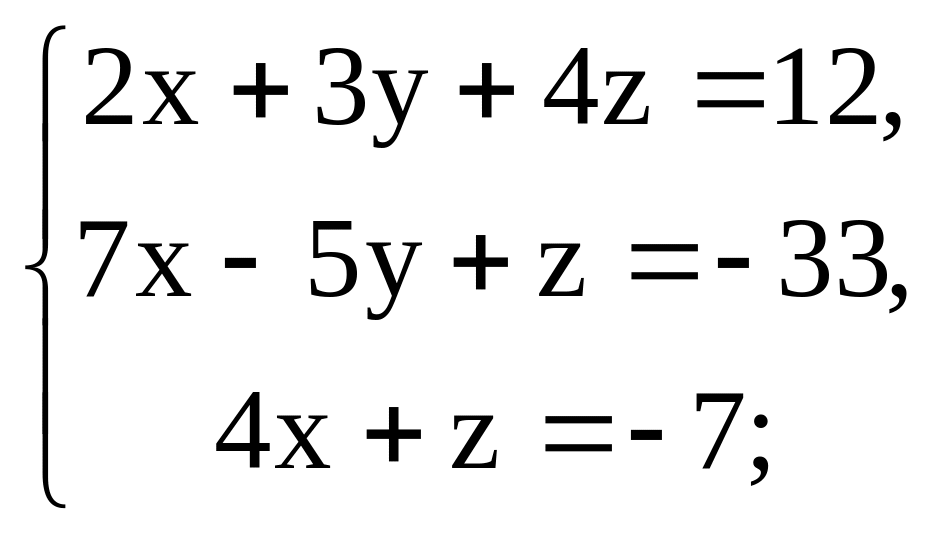
10.
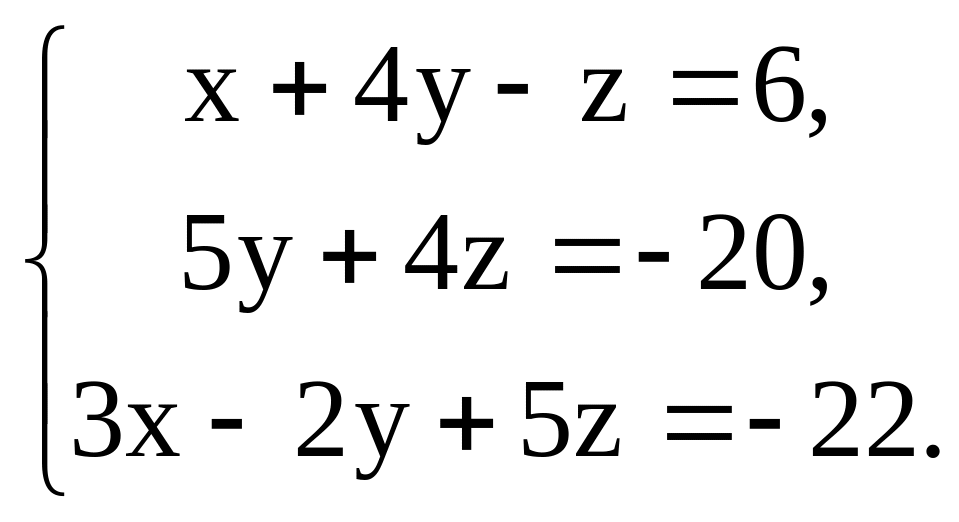
Задание 3.
Даны координаты пирамиды А1, А2, А3, А4.
Найти:
длину ребра А1, А2;
угол между ребрами А1, А2 и А1, А4;
площадь грани А1, А2, А3;
объем пирамиды;
уравнение прямой А1, А2;
уравнение плоскости А1, А2, А3.
Задание 4
Задача 4.
Задача на применение матриц в экономике
Найти
общую стоимость сырья, планируемую для
производства продукции двух видов
![]() и
и
![]() ,
если план выпуска продукции задан
матрицей
,
если план выпуска продукции задан
матрицей
![]() ;
нормы расхода сырья трех типов
;
нормы расхода сырья трех типов
![]() ,
,
![]() ,
,
![]() на единицу продукции
на единицу продукции
![]() заданы
матрицей
заданы
матрицей
![]() и известна стоимость сырья каждого вида
– матрица
и известна стоимость сырья каждого вида
– матрица
![]() .
.
4.1.
![]() ,
,
![]() ,
,
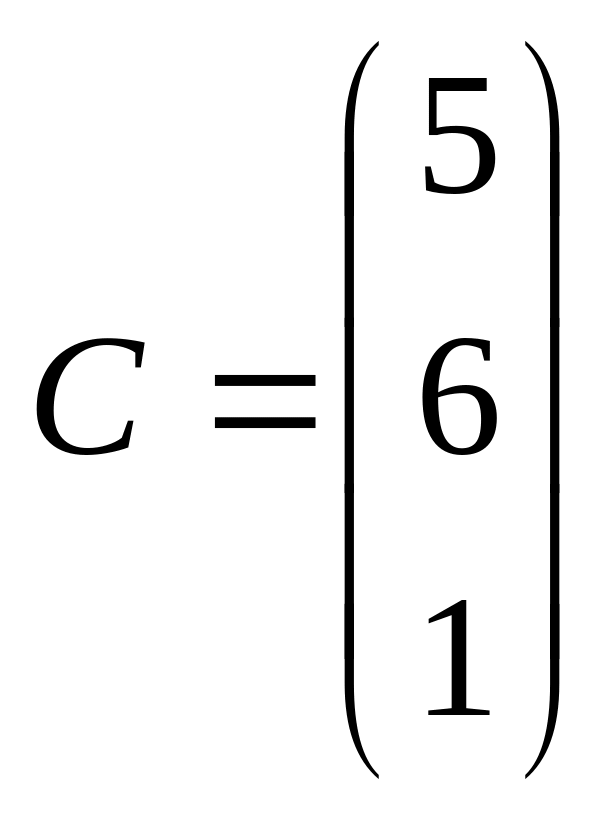
4.2.
![]() ,
,
![]() ,
,
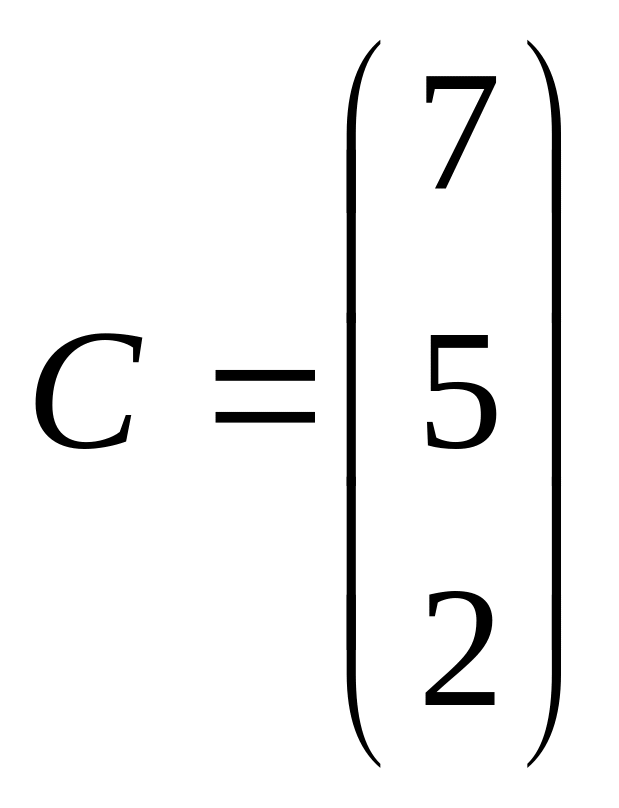
4.3.
![]() ,
,
![]() ,
,

4.4.
![]() ,
,
,
,

4.5.
![]() ,
,
![]() ,
,
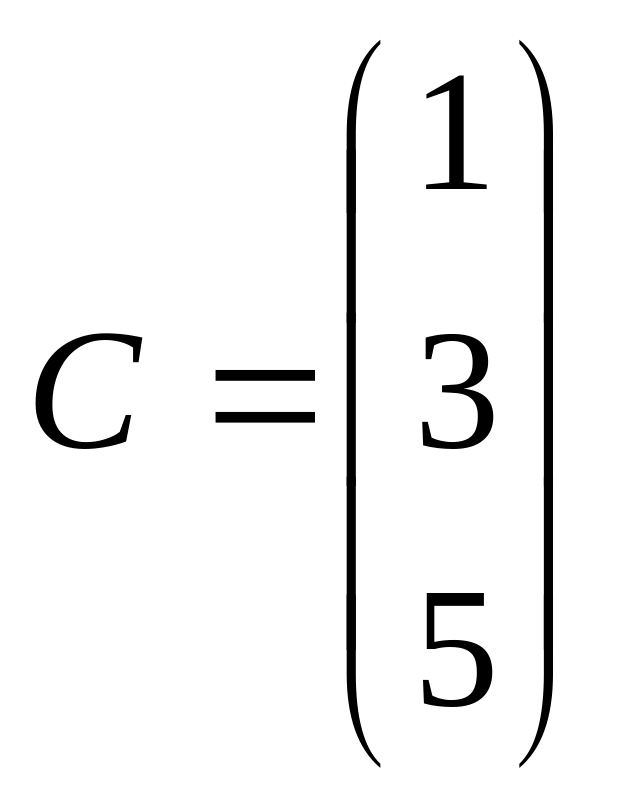
4.6.
![]() ,
,
![]() ,
,
4.7.
![]() ,
,
![]() ,
,
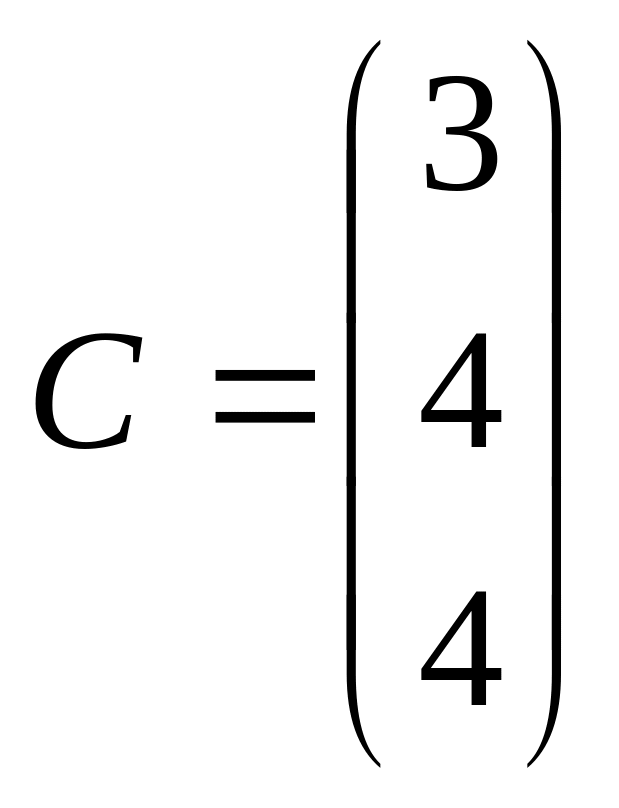
4.8.
![]() ,
,
![]() ,
,
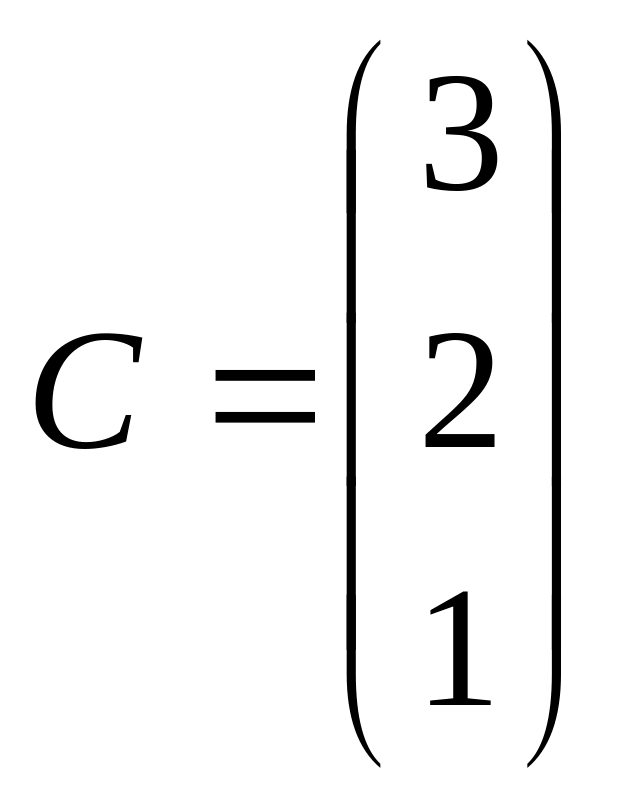
4.9.
,
![]() ,
,
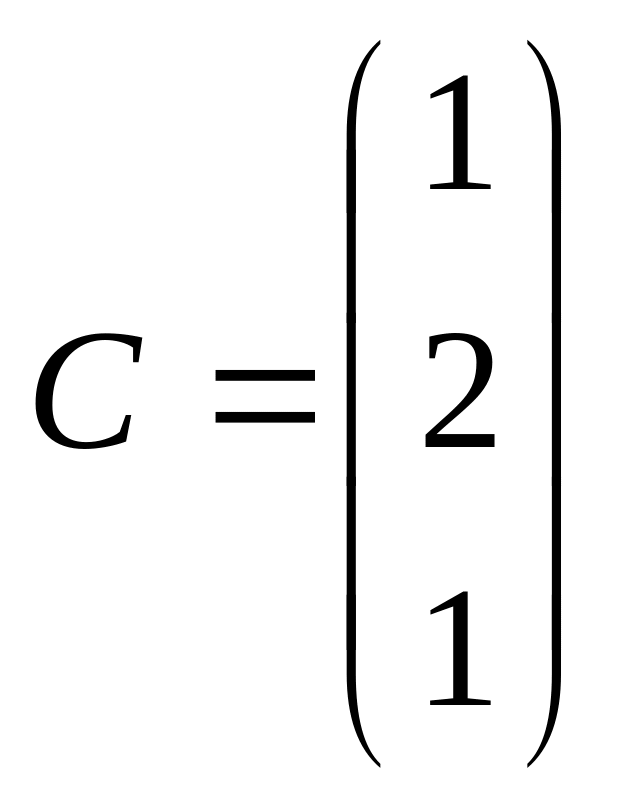
4.10. , ,
4.11.
![]() ,
,
,
,

4.12.
,
![]() ,
,

4.13.
,
![]() ,
,

4.14.
,
![]() ,
,

4.15.
![]() ,
,
![]() ,
,

4.16.
![]() ,
,
![]() ,
,
4.17.
![]() ,
,
![]() ,
,
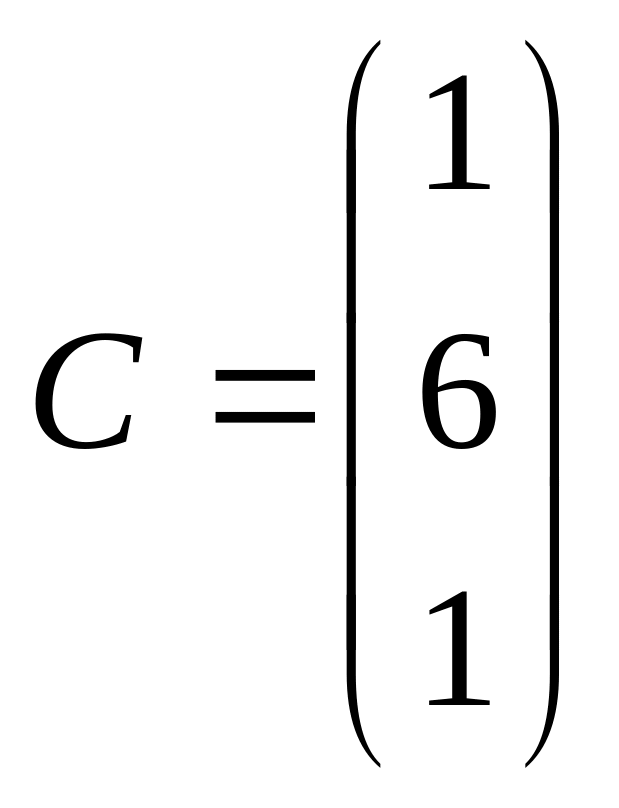
4.18.
![]() ,
,
![]() ,
,

4.19.
,
![]() ,
,

4.20. , ,
Задача 5.
Даны
точки А, В, С, D.
Найти координаты и длину вектора ![]() .
Построить вектор
.
.
Построить вектор
.
5.1.
А(-1,0 ,2 ), В( 1,2 ,1 ), С(3 , 7,-1 ), D(4
,6 ,5 ),
![]()
5.2.
А(2,0,-1), В(-1,2,1), С(-1,3,7), D(5,6,4),
![]()
5.3.
А(2,2,0), В(1,-2,1), С(3,-2,5), D(0,4,-2),
![]()
5.4.
А(0,-1,2), В(3,1,0), С(-3,0,0), D(4,5,-6),
![]()
5.5.
А(1,2,3), В(2,-1,0), С(3,0,3), D(7,-2,5),
![]()
5.6.
А(2,-3,1), В(0,2,2), С(-1,-1,0), D(0,6,0),
![]()
5.7.
А(0,1,4), В(3,-2,7), С(2,5,-3), D(4,4,0),
![]()
5.8.
А(3,4,3), В(0,0,1), С(2,7,6), D(5,-1,-2),
![]()
5.9.
А(4,0,1), В(6,-2,5), С(-3,0,-3), D(7,1,2),
![]()
5.10.
А(0,2,-3), В(1,-4,-6), С(7,2,2), D(0,5,0),
![]()
5.11. А(-1,0 ,2 ), В( 1,2 ,1 ), С(3 , 7,-1 ), D(4 ,6 ,5 ),
5.12. А(2,0,-1), В(-1,2,1), С(-1,3,7), D(5,6,4),
5.13. А(2,2,0), В(1,-2,1), С(3,-2,5), D(0,4,-2),
5.14. А(0,-1,2), В(3,1,0), С(-3,0,0), D(4,5,-6),
5.15. А(1,2,3), В(2,-1,0), С(3,0,3), D(7,-2,5),
5.16. А(2,-3,1), В(0,2,2), С(-1,-1,0), D(0,6,0),
5.17. А(0,1,4), В(3,-2,7), С(2,5,-3), D(4,4,0),
5.18. А(3,4,3), В(0,0,1), С(2,7,6), D(5,-1,-2),
5.19. А(4,0,1), В(6,-2,5), С(-3,0,-3), D(7,1,2),
5.20. А(0,2,-3), В(1,-4,-6), С(7,2,2), D(0,5,0),
Задача 1.
Решить матричное уравнение относительно неизвестной матрицы Х , если А, В, С, D, E - заданные матрицы:
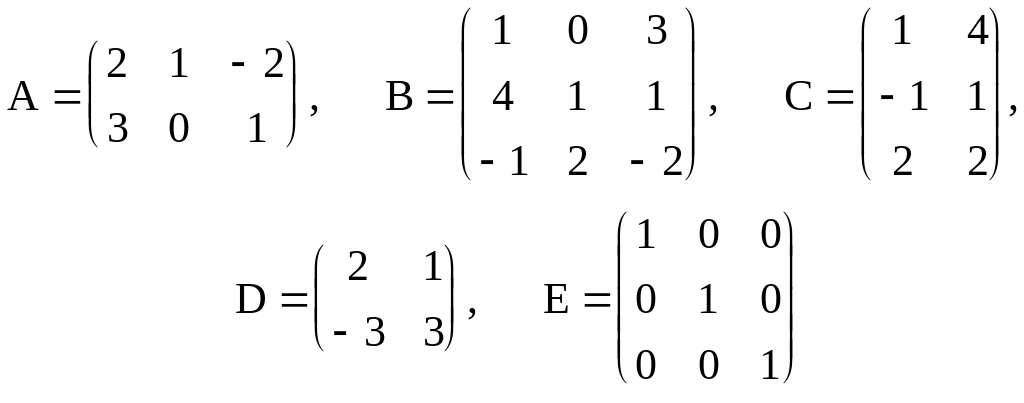
1.9. (A·B)T - 3·C = X
![]()



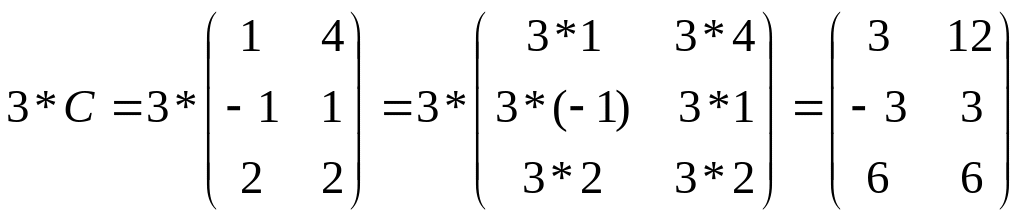
(A·B)T - 3·C = X

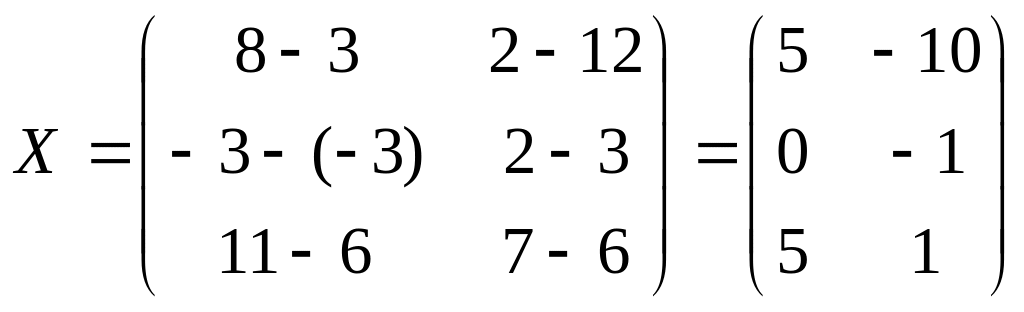
Задача 2.
Доказать, что данная система линейных уравнений имеет единственное решение. Найти по формулам Крамера. Сделать проверку.
2.9.
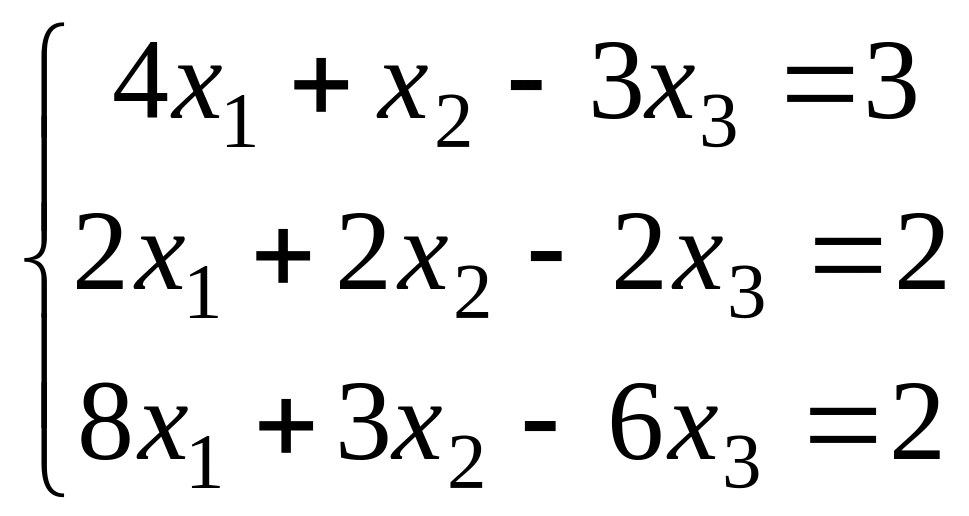
Запишем основную и расширенную матрицы для данной системы линейных уравнений, а также столбец свободных членов
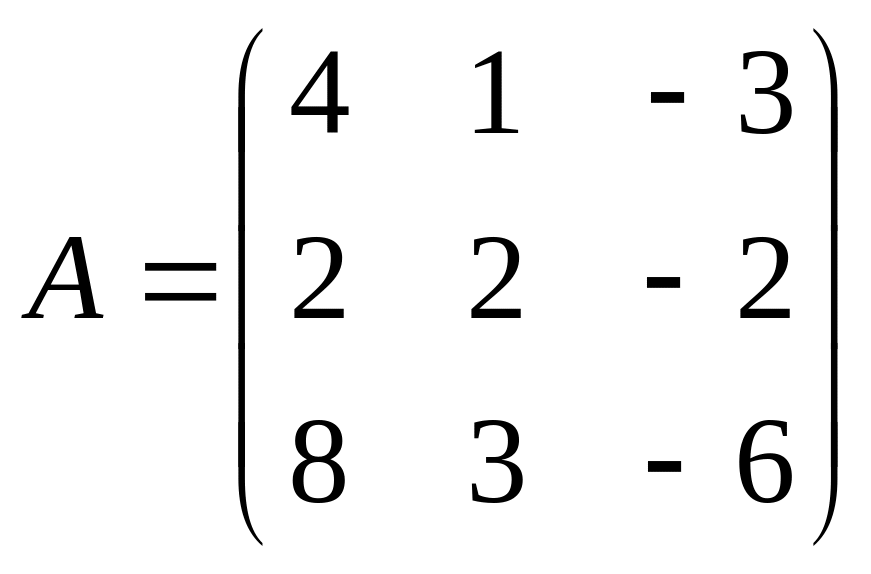

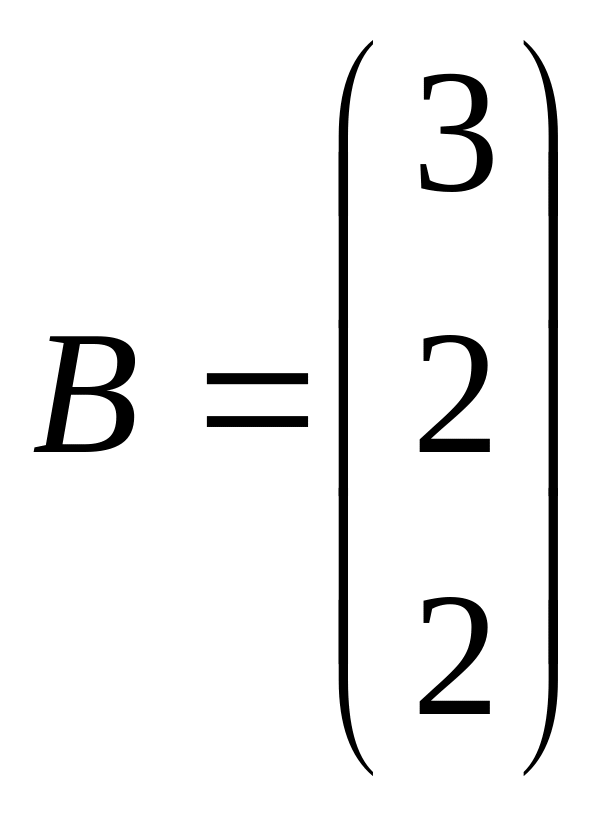
Найдем определитель основной матрицы
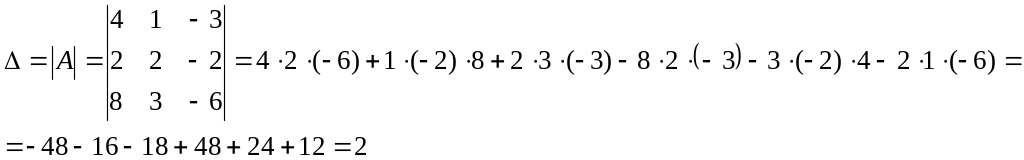
Так как найденный определитель отличен от нуля, то ранг матрицы А=3
Данный
определитель является минором матрицы
![]() , rang
A=rang
=3,
система совместна и имеет единственное
решение.
, rang
A=rang
=3,
система совместна и имеет единственное
решение.
Найдем решение системы методом Крамера:
|

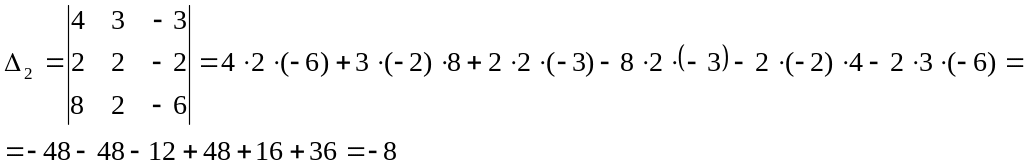
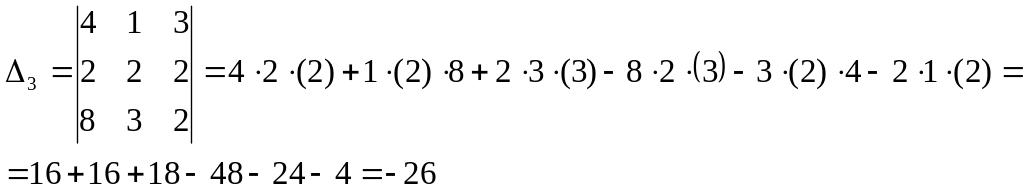
![]()
Проверка
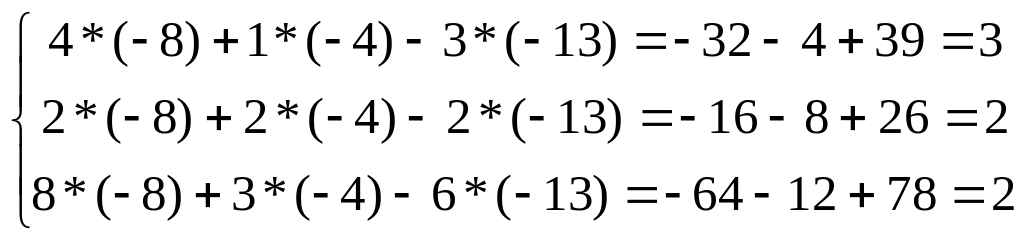
Задача 3.
Методом исключения ( методом Гаусса) исследовать совместность системы линейных уравнений и найти все ее решения.
3.9.
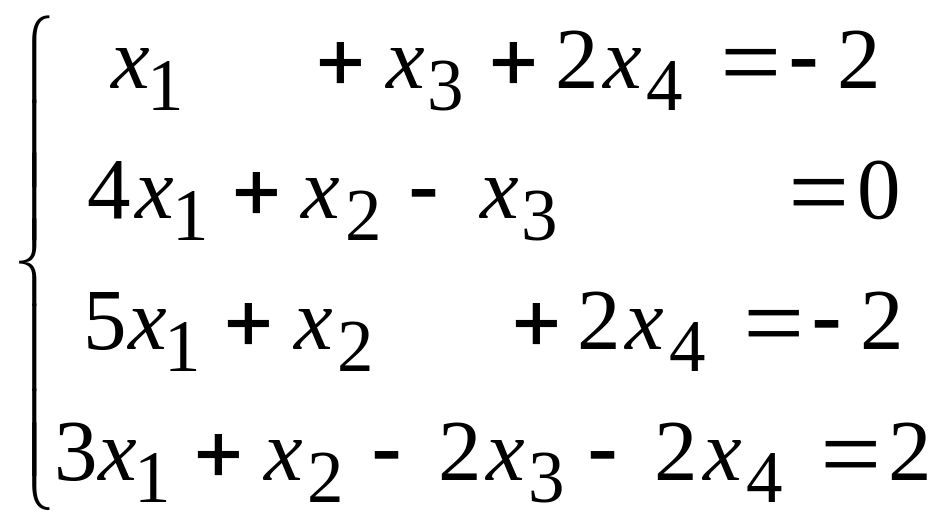
Решение:

![]()
![]()
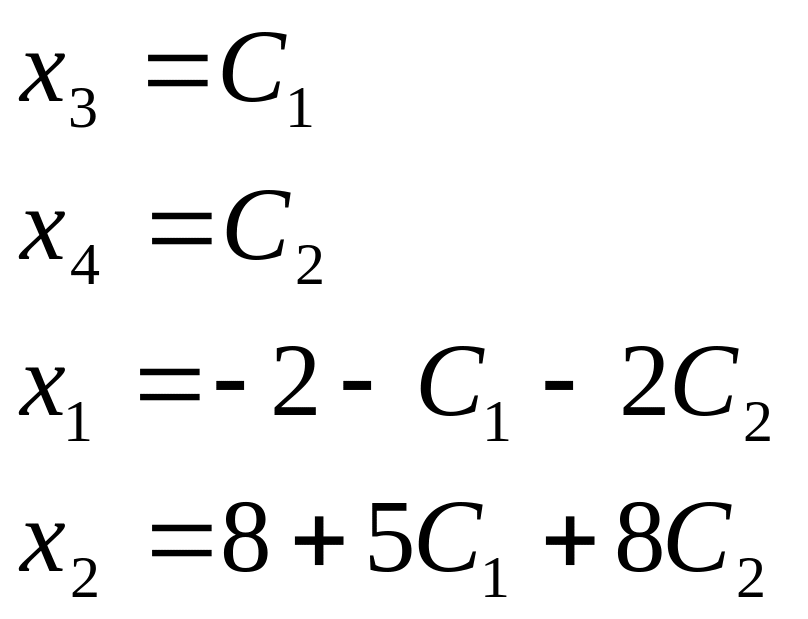
Задача 4.
Задача на применение матриц в экономике
Найти общую стоимость сырья, планируемую для производства продукции двух видов и , если план выпуска продукции задан матрицей ; нормы расхода сырья трех типов , , на единицу продукции заданы матрицей и известна стоимость сырья каждого вида – матрица .
4.9.
,
![]() ,
,
Общий расход материала
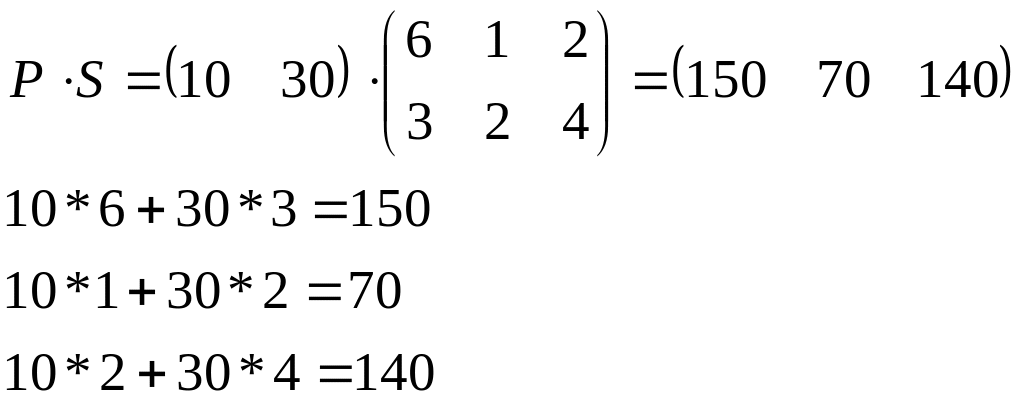
Общая стоимость заказа
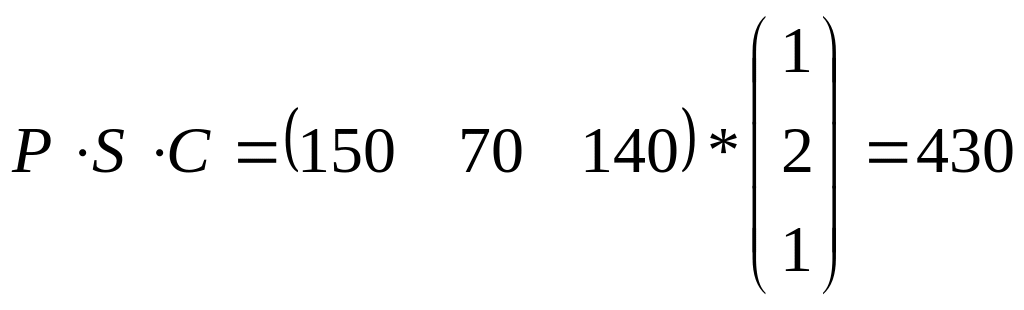
150*1+70*2+140*1=430
Задача 5.
Даны точки А, В, С, D. Найти координаты и длину вектора . Построить вектор .
5.9. А(4,0,1), В(6,-2,5), С(-3,0,-3), D(7,1,2),
решение:
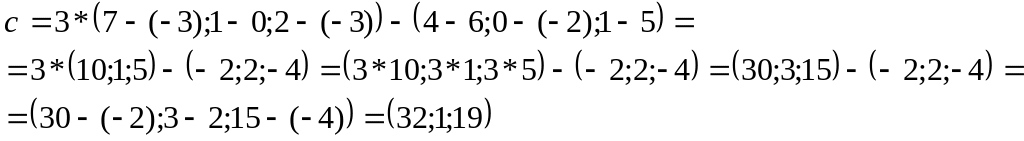
![]()
с(32;1;19)
z
у
х
