
- •Введение
- •Основные теоремы
- •Замечания
- •Соотношения между сторонами и углами треугольника. Неравенство треугольника
- •Решение плоских треугольников
- •Три стороны[править | править исходный текст]
- •Две стороны и угол между ними[править | править исходный текст]
- •Две стороны и угол не между ними[править | править исходный текст]
- •Сторона и прилежащие к ней углы[править | править исходный текст]
- •Сторона, прилежащий и противолежащий углы[править | править исходный текст]
Решение плоских треугольников

Стандартные обозначения в треугольнике
У
треугольника общего вида имеется 6
основных характеристик: 3 линейные
(длины сторон ![]() )
и 3 угловые (
)
и 3 угловые (![]() ),
см. рисунок. В классической задаче
плоской тригонометрии заданы 3 из этих
6 характеристик, и нужно определить 3
остальные. Очевидно, если известны
только 2 или 3 угла, однозначного решения
не получится, так как любой
треугольник, подобный данному,
тоже будет решением, поэтому будем
считать, что хотя бы одна из известных
величин — линейная.
),
см. рисунок. В классической задаче
плоской тригонометрии заданы 3 из этих
6 характеристик, и нужно определить 3
остальные. Очевидно, если известны
только 2 или 3 угла, однозначного решения
не получится, так как любой
треугольник, подобный данному,
тоже будет решением, поэтому будем
считать, что хотя бы одна из известных
величин — линейная.
Алгоритм решения задачи зависит от того, какие именно характеристики треугольника считаются известными. Далее будем символически обозначать заданные величины С (сторона) и У (угол). Поскольку сочетание УУУ исключено из рассмотрения, остаются 5 различных вариантов[2]:
Три стороны (ССС);
Две стороны и угол между ними (СУС);
Две стороны и угол не между ними (ССУ);
Сторона и два прилежащих угла (УСУ);
Сторона, противолежащий угол и один из прилежащих (УУС).

![]()
Заданы три стороны
Три стороны[править | править исходный текст]
Пусть
заданы длины всех трёх сторон
.
Чтобы найти углы ![]() ,
воспользуемся теоремой
косинусов[3]:
,
воспользуемся теоремой
косинусов[3]:
![]()
![]()
Третий угол сразу находится из правила, что сумма всех трёх углов должна быть равна 180°.
В некоторых источниках предлагается второй угол найти по теореме синусов, но, как указано в вышеприведенном замечании 1, при этом существует опасность спутать тупой угол с острым.
Ещё один метод вычисления углов по известным сторонам: использование теоремы котангенсов.

Заданы две стороны и угол между ними
Две стороны и угол между ними[править | править исходный текст]
Пусть,
для определённости, известны длины
сторон ![]() и
угол
и
угол ![]() между
ними. Для определения длины стороны
между
ними. Для определения длины стороны ![]() вновь
воспользуемсятеоремой
косинусов[4]:
вновь
воспользуемсятеоремой
косинусов[4]:
![]()
Мы фактически свели задачу к предыдущему случаю. Далее воспользуемся теоремой косинусов для нахождения второго угла:
Третий
угол ![]() .
.

Заданы две стороны и угол не между ними
Две стороны и угол не между ними[править | править исходный текст]
Этот
случай самый сложный и неоднозначный.
Пусть, например, известны две стороны ![]() и
угол
.
Уравнение для угла
найдём
изтеоремы
синусов[5]:
и
угол
.
Уравнение для угла
найдём
изтеоремы
синусов[5]:
![]()
Для
краткости обозначим ![]() (правая
часть уравнения). При решении уравнения
возможны 4 случая[6].
(правая
часть уравнения). При решении уравнения
возможны 4 случая[6].
Если
 ,
такого треугольника не существует
(сторона
,
такого треугольника не существует
(сторона  «не
достаёт» до линии BC).
«не
достаёт» до линии BC).Если
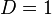 ,
существует единственное решение, причём
треугольник прямоугольный,
,
существует единственное решение, причём
треугольник прямоугольный, 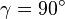
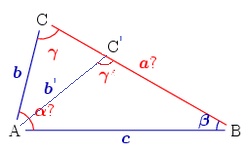
Два возможных решения
Если
 ,
то возможны 2 варианта.
,
то возможны 2 варианта.Если
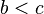 ,
то угол
имеет
два возможных значения: острый угол
,
то угол
имеет
два возможных значения: острый угол 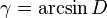 и
тупой угол
и
тупой угол 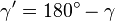 .
На рисунке справа первому значению
соответствуют точка
.
На рисунке справа первому значению
соответствуют точка 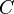 ,
сторона
и
угол
,
а второму значению — точка
,
сторона
и
угол
,
а второму значению — точка  ,
сторона
,
сторона  и
угол
и
угол  .
.Если
 ,
то
,
то  (как
известно, большей стороне треугольника
соответствует больший противолежащий
угол). Поскольку в треугольнике не
может быть двух тупых углов, тупой угол
для
исключён,
и решение
единственно.
(как
известно, большей стороне треугольника
соответствует больший противолежащий
угол). Поскольку в треугольнике не
может быть двух тупых углов, тупой угол
для
исключён,
и решение
единственно.
Третий
угол находится как обычно: ![]() .
Третью сторону можно найти по теореме
синусов:
.
Третью сторону можно найти по теореме
синусов:
![]()

Заданы сторона и прилежащие к ней углы
