3 Расчетно-графическая работа №2. Расчет линии с распределенными параметрами

Задана линия с первичными параметрами (R₀, G₀, L₀, C₀) и частотой f, длиной линии l. Известен ток в конце линии (I₂) и сопротивление нагрузки (R_н).

Определить:

1) Вторичные параметры линии.

2) Напряжение и ток в начале линии.

3) Активную мощность в начале и конце линии, кпд линии.

Полагая, что линия стала линией без потерь, определить:

1) Вторичные параметры линии.

2) Напряжение и ток в начале линии.

Т а б л и ц а 3.1

Год поступления		Последняя цифра зачетной книжки
чётный	1		2	3	4	5	6	7	8	9	0
нечётный	0		9	8	7	6	5	4	3	2	1
R0, Ом/км	1		3	5	7	9	2	4	6	8	10
L0, мГн/км	0.5		1	1.5	2	0.8	1.2	1.7	2.1	2.3	2.7
f, кГц	1		2	3	4	5	1	2	3	4	5

Т а б л и ц а 3.2

Год поступления	Предпоследняя цифра зачетной книжки
чётный	1	2	3	4	5	6	7	8	9	0
нечётный	0	9	8	7	6	5	4	3	2	1
G0, мкСм/км	1.1	1.2	1.3	1.4	1.5	1.6	1.7	1.8	1.9	2.1
Rн, Ом	400	350	300	250	200	150	100	50	450	500

Т а б л и ц а 3.3

Год поступления	Первая буква фамилии
чётный	БЛЦ	КХ	ВМЧ	ГНШ	ДОЯ	ЕПР	ЖСЗ	ТЭИ	УЮФ	АЩ
нечётный	КХ	ВМЧ	ГНШ	БЛЦ	ЕПР	ДОЯ	ТЭИ	ЖСЗ	АЩ	УЮФ
l, км	100	95	90	85	80	75	70	65	60	55
С, нФ/км	4	4.5	5	5.5	6	6.5	7	7.5	8	8.5
I2, мА	100	90	80	70	60	50	40	30	20	10

4 Методические указания к выполнению расчетно-графических работ № 1,2

Каскадное соединение является наиболее часто встречающимся в цепях автоматики, связи и телемеханики.

Для определения параметров четырехполюсника, получившегося в результате каскадного соединения через параметры отдельных четырехполюсников наиболее удобно пользоваться системой -параметров. При этом матрица -параметров всего соединения определяется как произведение матриц -параметров составляющих этого соединения. Другими словами, для определения какого-либо -параметра каскадного соединения необходимо перемножить соответствующие -параметры отдельных четырехполюсников.

При каскадном (цепочечном) соединении четырехполюсников входные зажимы каждого последующего четырехполюсника подключаются к выходным зажимам предыдущего.

Рисунок 3.1

, , ,

Рисунок 3.2

Коэффициенты четырехполюсника могут быть определены по известным напряжениям и токам из режимов холостого хода и короткого замыкания из системы уравнений -параметров.

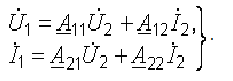
Коэффициенты пассивного четырехполюсника связаны соотношением:

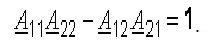
Входное сопротивление представляет собой то сопротивление, которое является нагрузкой для генератора, подключенного к четырехполюснику.

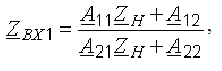
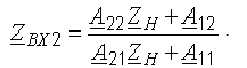
Вторичные параметры четырехполюсника через А-параметры:

^.

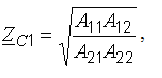
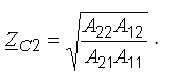
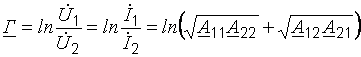Характеристические сопротивления можно выразить через параметры холостого хода и короткого замыкания:

, .

Характеристическая постоянная передачи через параметры холостого хода и короткого замыкания:

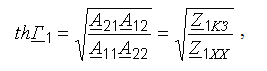
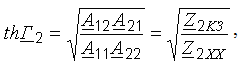
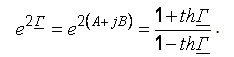
Вторичные (характеристические) параметры линии: 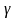- коэффициент распространения волны. Он характеризует изменение напряжения 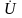и тока вдоль линии на протяжении 1 км. В алгебраической форме комплекс

,

где - коэффициент затухания волны на 1 км, ;

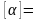
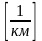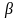- коэффициент изменения фазы на 1 км, .

Волновое или характеристическое сопротивление линии:

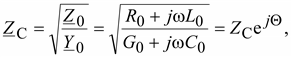
Зная ток и напряжение в конце линии, можно определить ток и напряжение в начале линии:

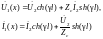
Если положить R₀= G₀=0, то получим так называемую линию без потерь.

Для такой линии все найденные соотношения упрощаются, продольное сопротивление и поперечная проводимость на единицу длины линии будут

.

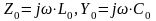Тогда волновое сопротивление линии: ,

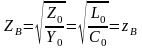т.е. оказывается чисто вещественным числом, не зависящим от частоты генератора, питающего линию. Следовательно, токи падающей и отраженной волн совпадают по фазе со своими напряжениями.

Коэффициент распространения на единицу длины линии оказывается числом мнимым ,

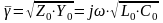т.е. коэффициент затухания , коэффициент изменения фазы:

.
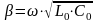