4.8. Пассивное интегрирующее звено

Представив пассивное интегрирующее звено (см. рис. 4.3.) в виде делителя напряжения получим передаточную функцию аналогичную (4.23):

w

Рис. 4.3. Пассивное интегрирующее звено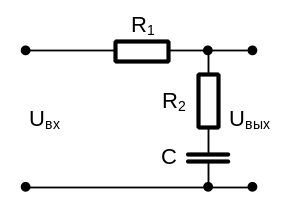

_из(p) = z₂(p) / (z₁(p) + z₂(p)), (4.26)

где z₁(p) = R₁ – полное сопротивление первого плеча делителя; z₂(p) = R₂ + (1 / pC) полное сопротивление второго (выходного) плеча делителя см. рис. 4.3., здесь 1 / pC – операторная форма записи полного сопротивления на емкости С.

Подставим z₁(p) и z₂(p) и выполним перегруппировку в выражении передаточной функции (4.26), получим:

. (4.27)

Введем постоянные времени Т₁ = R₂ С и Т₂ = C (R₁ + R₂). В итоге получим передаточную функцию пассивного интегрирующего звена в операторной форме:

. (4.28)

4.9. Пассивное индуктивное звено

Представив пассивное индуктивное звено (см. рис. 4.4.) в виде делителя напряжения получим передаточную функцию аналогичную (4.23):

w_инз(p) = z₂(p) / (z₁(p) + z₂(p)), (4.29)

где z₂(p) = R₂ – полное сопротивление второго (выходного) плеча делителя; z₁(p) = pL + R₁ полное сопротивление первого плеча делителя см. рис. 4.4., здесь pL – операторная форма записи полного сопротивления на индуктивности L.

П

Рис. 4.4. Пассивное индуктивное звено

одставим z₁(p) и z₂(p) и разделим слагаемые в числителе и знаменателе выражения передаточной функции (4.29) на (R₁ + R₂), получим:

.(4.30)

Введем коэффициент передачи k_инз = R₂ / (R₁ + R₂) и постоянную времени Т_инз = L / (R₁ + R₂). В итоге получим передаточную функцию пассивного индуктивного звена, как апериодического звена первого порядка:

. (4.31)

4.6. Тахогенератор

Напряжение тахогенератора пропорционально скорости вращения его вала. У реального датчика скорости вращения основанного на этом устройстве имеется небольшая постоянная времени и некоторая нелинейность характеристики. В рамках данной работы будем считать элемент обратной связи (тахогенератор) – безынерционным звеном. В этом случае уравнение описывающее работу тахогенератора имеет вид:

U_тг = k_тг n, (4.32)

где U_тг – напряжение на зажимах тахогенератора (выходная величина); k_тг ‑ коэффициент передачи тахогенератора; n – обороты вала (входная величина).

Передаточная функция тахогенератора как безынерционного звена будет иметь вид:

w_тг(p) = k_тг. (4.33)

4.10. Датчик напряжения

Датчик напряжения см. рис. 4.4 представляет собой электромагнитную катушку (1) с подвижным сердечником (2). На катушку подается постоянное входное напряжение U_вх. Сердечник жестко соединен с потенциометром (3) и перемещается совместно с ним вдоль продольной оси. Возвратная пружина (4) противодействует выталкивающей электромагнитной силе катушки, действующей на сердечник. Жестко закрепленный ползунок потенциометра (5) перемешается по подвижному резистору (3) и изменяет значение выходного сопротивления R_вых в зависимости от величины U_вх.

З

Рис. 4.4. Датчик напряжения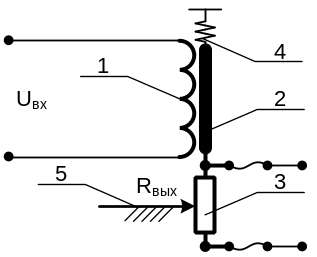

начение выходного сопротивления R_вых в основном зависит от падений входного напряжения (U_вх) в цепи катушки и механического сопротивления возвратной пружины, поэтому для описания его работы и вывода передаточной функции необходимо иметь два исходных дифференциальных уравнения.

Первое уравнение может быть получено на основании записи второго закона Кирхгофа для цепи катушки:

L_к (dI_к / dt) + R_к I_к = U_вх, (4.34)

где L_к – индуктивность катушки; I_к – ток в обмотке катушки; R_к – активное сопротивление катушки; U_вх – напряжение на катушки (входная величина).

Второе уравнение выведем на основании закона равновесия сил действующих на якорь катушки, оно имеет вид:

F_м – F_п = 0, (4.35)

где F_м – электромагнитная сила катушки. F_п – возвратная сила пружины; Так как возвратная сила пружины F_п зависит от степени ее растяжения, вызванным приращением силы F_м, то для дальнейших преобразований можно сделать допущение, что величина R_вых линейно зависит от значения силы F_м. Тогда расчетное уравнение будет иметь вид:

R_вых = k_r (F_м), (4.36)

где k_r – коэффициент пропорциональности между силой F_м и R_вых.

F_м = k_к I_к², (4.37)

где k_к – коэффициент пропорциональности учитывающий конструкцию катушки и сердечника; I_к – ток в обмотке катушки.

Уравнение (4.37) нелинейно, его необходимо линеаризовать. Введем малые отклонения всех переменных участвующих в расчете:

U_вх = U₀ + u_вх, R_вых = R₀ + r_вых, F_м = F₀ + f, I_к = I₀ + i, (4.38)

где u_вх, r_вых, f, i – малые отклонения соответствующих переменных от известного установившегося значения, обозначенного нижним индексом 0.

Разложим уравнение (4.37) в ряд Тейлора и получим уравнение динамики в малых отклонениях:

, (4.39)

где k_м = 2k_кI₀ – постоянный коэффициент;  - высшие слагаемые ряда, согласно общего метода линеаризации их отбрасывают, подробно см. [1].

Подставим (4.39), с учетом (4.38), в (4.36) и в результате получим второе линеаризованное уравнение в малых отклонениях:

r_вых = k_r k_м i. (4.40)

Первое уравнение (4.34) в операторной форме, с учетом (4.38), будет иметь вид:

((L_к / R_к) p + 1) i = (1 / R_к) u_вх, (4.41)

Решим совместно (4.40) и (4.41) и в результате получим:

((L_к / R_к) p + 1) r_вых = (k_r k_м / R_к) u_вх, (4.42)

Введем новые обозначения и перейдем к стандартной форме записи дифференциального уравнения:

(T_дн p + 1) r_вых = k_дн u_вх , (4.43)

где T_дн – постоянная времени цепи катушки датчика (T_дн = L_к / R_к); k_д – коэффициент передачи датчика (k_дн = k_r k_м / R_к).

Передаточная функция датчика напряжения, как апериодического звена первого порядка, будет иметь вид:

w_дн(p) = k_дн / (T_дн p + 1). (4.44)

В пояснительной записке для всех динамических звеньев функциональной схемы САР, по варианту задания, записываются исходные уравнения, и делается полный вывод передаточных функций. В конце каждого пункта (динамического звена) должны быть записаны итоговые передаточные функции (с заданными численными значениями постоянных времени и коэффициентов передачи).