4.2. Элемент сравнения

В рассматриваемом примере (рис. 2.1) в качестве элемента сравнения используется схема вычитания двух напряжений.

Уравнение, связывающее входное напряжение усилителя с задающим напряжением и напряжением цепи обратной связи, имеет вид:

U = U_з – U_тг. (4.1)

Чаше всего при расчетах систем автоматической стабилизации работающих по замкнутому циклу считается, что элемент сравнения идеален, т. е. не вносит погрешность в процесс регулирования. Данное допущение не сказывается на точности, так как погрешность элемента сравнения можно учесть в виде дополнительного возмущающего воздействия в замкнутой системе.

4.3. Электронный усилитель

Рассматривать уравнение, описывающее работу электронного усилителя, можно только при наличии его принципиальной схемы. Кроме того, так как электронные усилители имеют очень малую инерционность, то ее величиной обычно пренебрегают, считая усилитель безынерционным звеном. В результате имеем:

U_эу = k_эу U_вх, (4.2)

где U_вх – напряжение на входе электронного усилителя (U в рассматриваемом примере); U_эу – напряжение на выходе усилителя; k_эу – коэффициент передачи электронного усилителя.

Передаточная функция звена для электронного усилителя с уравнением (4.2) будет иметь вид:

w_эу(p) = k_эу. (4.3)

В некоторых вариантах задания на курсовой проект электронный усилитель имеет постоянную времени T_эу отличную от нуля. В этом случае для электронного усилителя следует использовать передаточную функцию апериодического звена первого порядка, которая имеет вид:

w_эу(p) = k_эу / (T_эу p + 1). (4.4)

4.4. Генератор постоянного тока независимого возбуждения

Генератор независимого возбуждения можно представить как в виде одного типового динамического звена, так и в виде двух звеньев включенных последовательно. Рассмотрим генератор в виде двух динамических звеньев. Передаточную функцию для генератора – одного звена можно будет получить перемножением передаточных функций отдельных его составляющих.

Обмотка возбуждения. Дифференциальное уравнение на основании второго закона Кирхгофа для цепи возбуждения генератора имеет вид:

L_в (dI_в / dt) + R_вI_в = U_вх, (4.5)

где L_в – индуктивность обмотки возбуждения; I_в – ток в обмотке возбуждения (выходная величина); R_в – активное сопротивление обмотки возбуждения; U_вх – напряжение на обмотке возбуждения (входная величина).

Разделим уравнение на произведение R_вI_в, в результате получим:

(L_в dI_в) / (R_вI_в dt) + (R_вI_в) / (R_вI_в) = U_вх / (R_вI_в). (4.6)

Выполним сокращения и перейдем к операторной форме записи:

(L_в / R_в) p + 1 = U_вх / (R_вI_в), (4.7)

где p – оператор Лапласа.

Умножим обе части выражения на I_в и приведем уравнение к стандартному виду:

(T_ов p + 1) I_в = U_вх k_ов. (4.8)

где T_ов – постоянная времени цепи возбуждения генератора постоянного тока, T_ов = (L_в / R_в); k_ов – коэффициент передачи обмотки возбуждения генератора, k_ов = (1 / R_в).

Передаточная функция обмотки возбуждения, как апериодического звена первого порядка, имеет вид:

w_ов(p) = k_ов / (T_ов p + 1). (4.9)

Якорь генератора - безынерционное звено. Данный вариант передаточной функции соответствует исходным данным на курсовой проект, когда постоянная времени T_г для цепи якоря равна нулю. На основании известной характеристики генератора независимого возбуждения (рис. 4.1) можно определить коэффициент передачи для цепи якоря.

Е

Рис. 4.1. Характеристика генератора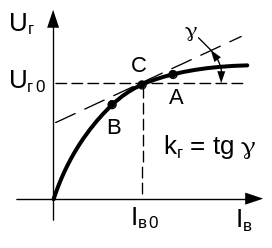

сли из анализа работы САР известно, что ток возбуждения и напряжение на якоре в процессе работы мало отклоняются от нулевых начальных условий, то можно воспользоваться методом графической линеаризации.

На характеристике отмечается рабочая точка с координатами (I_в0, U_г0), которые соответствуют нулевым начальным условиям. Через эту точку проводится касательная к криволинейной характеристике генератора. Тангенс угла наклона данной касательной и будет являться коэффициентом передачи якоря генератора.

Таким образом, на основании метода графической линеаризации имеем линеаризованное уравнение:

U_г = I_в tg  = k_г I_в, (4.10)

где U_г - напряжение на зажимах якоря генератора (выходная величина);  ‑ угол наклона касательной к характеристике генератора в рабочей точке; k_г ‑ коэффициент передачи якоря генератора.

На самом деле на якорь генератора со стороны статора воздействует магнитный поток Ф. В рамках курсового проекта будем считать, что ток возбуждения I_в и магнитный поток Ф, в рабочей области, связаны линейной зависимостью и их коэффициент пропорциональности учтен в k_г.

Передаточная функция якоря генератора как безынерционного звена будет иметь вид:

w_г(p) = k_г. (4.11)

В некоторых вариантах задания на курсовой проект якорь генератора имеет постоянную времени T_г отличную от нуля. В этом случае для якоря генератора следует использовать передаточную функцию апериодического звена первого порядка, которая имеет вид:

w_г(p) = k_г / (T_г p + 1). (4.12)