10. Построение кривой переходного процесса

10.1. Общие положения

В результате изменения управляющего или возмущающего воздействия в системе автоматического регулирования наблюдается переходный процесс, заключающийся в переходе от одного установившегося состояния САР к другому.

Кривой переходного процесса называют зависимость регулируемой величины от времени при переходе от одного установившегося состояния к другому.

Частотный метод расчета переходных процессов в САР применяется при анализе качества регулирования. Он является графоаналитическим методом и позволяет с достаточной точностью рассчитывать переходные процессы в системах практически любой сложности.

С помощью частотного метода, разработанного В.В. Солодовниковым, по известной вещественной характеристике системы P() можно построить кривую переходного процесса X(t):

. (10.1)

Вещественной частотной характеристикой называют зависимость вещественной части частотной передаточной функции замкнутой САР при изменении частоты от нуля до бесконечности.

Прямое интегрирование выражения (10.1), даже с использованием компьютера, связано с большими временными затратами. Поэтому на практике используются приближенные методы решения этой задачи.

Для этой цели вводится понятие единичной трапецеидальной вещественной характеристики.

Единичная трапецеидальная вещественная характеристика представляет собой прямоугольную трапецию, имеющую высоту и частоту среза равную единице. Кроме того, данная трапеция характеризуется коэффициентом наклона своей боковой грани подробнее см. [1].

Для единичных трапеций с различными коэффициентами наклона боковой грани по выражению (10.1) рассчитано большое количество функций времени. Эти функции получили название h-функций.

H-функции это кривые переходного процесса, соответствующие единичным трапецеидальным вещественным характеристикам с разным коэффициентом наклона боковой грани.

H-функций сведены в специальные таблицы, которые приводятся в специальной литературе, например [4, стр. 298–299]. По такой таблице для различных коэффициентов наклона боковой грани единичной трапеции может быть построена искомая функция времени h(t₀).

Рассмотрим порядок построения кривой переходного процесса методом трапецеидальных вещественных характеристик. Метод построения заключается в том, что имеющуюся вещественную характеристику исследуемой системы заменяют на несколько прямоугольных трапеций, затем их соотносят с h-функциями, и полученные в результате кривые суммируют.

10.2. Построение вещественной частотной характеристики сар

Для рассматриваемого примера передаточная функция замкнутой системы, в операторной форме, имеет вид:

, (10.2)

где a₀ … a₃ – численные значения коэффициентов.

Перейдем к частотной передаточной функции замкнутой САР, для чего выполним подстановку значения p = j. В результате, получим следующее комплексное число, содержащее мнимую часть в знаменателе:

. (10.3)

Для того чтобы избавиться от мнимости в знаменателе выражения (10.3), умножим числитель и знаменатель дробной функции на комплексное число, сопряженное комплексному числу в знаменателе:

. (10.4)

В результате алгебраического преобразования мнимая часть в знаменателе исчезнет, а в числителе наоборот появится. В итоге можно разделить выражение (10.3) на вещественную и мнимую части:

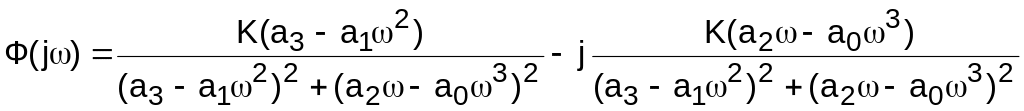. (10.5)

Выделив из формулы (10.5) вещественную часть, получим выражение для построения вещественной частотной характеристики рассматриваемой системы:

. (10.6)

На рис. 10.1 изображена примерная вещественная частотная характеристика рассматриваемой САР.

Для построения графика вещественной характеристики необходимо в формулу (10.6) подставлять значения частоты в диапазоне от нуля до бесконечности (последнее значение частоты должно соответствовать значению P() равному приблизительно 1 … 3 процента ее максимальной ординаты).

Масштаб по осям абсцисс и ординат на рис. 10.1. указан произвольный, его наличие необходимо для наглядности дальнейшего процесса построения кривой переходного процесса в рассматриваемом варианте.

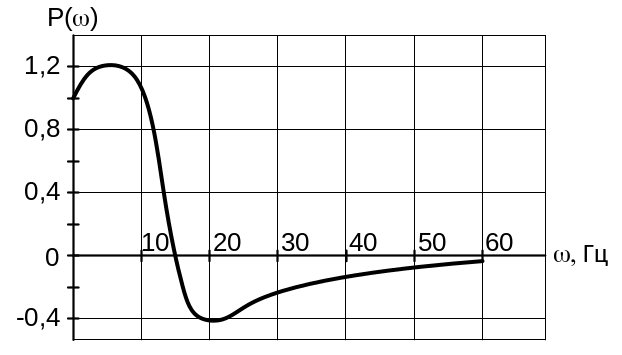
Рис. 10.1. Вещественная частотная характеристика системы

В пояснительной записке курсового проекта, в соответствии с вариантом задания, должен быть отражен вывод выражения аналогичного формуле (10.6) и на отдельном графике построена вещественная частотная характеристика системы.