8.3. Построение лфх

Построение ЛФХ рекомендуется выполнять в математическом пакете (Maple, MathLab или аналогичных), или вручную с использованием MS Excel. Вне зависимости от метода построения характеристик на графиках должны полностью отражаться все изменения исследуемой функции.

ЛФХ для рассматриваемого примера строится по выражению (8.7), в формулу (8.7) подставлять значения частоты от нуля до бесконечности.

Последнее значение частоты при построении ЛФХ должно соответствовать фазовому сдвигу менее минус ста девяноста градусов,т.е. ЛФХ должна пересечь ось частот.

Расчет и построение ЛФХ необходимо выполнять в градусах, а частоту на ЛАХ и ЛФХ выражать в герцах (логарифмический масштаб).

8.4. Оценка устойчивости системы по лах и лфх

В абсолютно устойчивых системах фазовый сдвиг может достигать значения минус 180 только при модулях, меньших единицы. Это заключение позволяет легко оценить устойчивость системы по виду ЛАХ и ЛФХ разомкнутой САР.

Для того чтобы САР была устойчива, точка пересечения ЛАХ со значением нуля децибел должна лежать левее точки, где фазовый сдвиг достигает значения в минус сто восемьдесят градусов. Если это условие не выполняется, то система будет неустойчива. Для устойчивых САР построенные рис. 8.1. графики ЛАХ и ЛФХ позволяют оценить запас устойчивости - два отрезка  и L отражают по фазе и амплитуде соответственно первый выражается в градусах второй в децибелах.

Если эти две точки для ЛАХ и ЛФХ совпадают, то система находится на границе колебательной устойчивости. В условно устойчивых системах фазовый сдвиг может достигать значения минус 180 четное количество раз.

В пояснительной записке курсового проекта необходимо представить:

• исходную формулу для построения ЛАХ;

• порядок построения асимптотической ЛАХ для своего варианта (если строится приближенная ЛАХ);

• исходную формулу для построения ЛФХ;

• графики ЛАХ и ЛФХ, построенные на одной стандартной координатной сетке (см. пункт 8.1);

• вывод об устойчивости или неустойчивости САР по виду ЛАХ и ЛФХ, а также о возможной границе устойчивости;

• для устойчивой САР на графиках ЛАХ и ЛФХ указать запас устойчивости по фазе  и по амплитуде L.

9. Анализ устойчивости сар методом д-разбиения

При проектировании системы автоматического регулирования иногда бывает необходимо исследовать влияние различных ее параметров на устойчивость системы в целом. Для решения этой задачи используется метод построения областей устойчивости, то есть определение областей значений параметров, при которых система оказывается устойчивой.

Исследование устойчивости методом Д-разбиения основано на решении характеристического уравнения системы относительно одного или двух параметров.

По заданию преподавателя в рамках курсового проекта надлежит выполнить построение области устойчивости для коэффициента усиления системы автоматического регулирования.

Для характеристического уравнения рассматриваемого примера (6.5), справедлива замена a₃ = K + 1, следовательно, имеем:

а₀р³ + а₁р² + а₂р + K + 1 = 0, (9.1)

где a₀ … a₂ – численные значения коэффициентов; K – коэффициент усиления САР. Решая уравнение (9.1) относительно параметра K, будем иметь следующее выражение:

K = –(a₀p³ + a₁p² + a₂p + 1). (9.2)

Подставим в формулу (9.2) значение p = j разложим ее на вещественную и мнимую часть, в итоге получим:

K = А() + jВ(). (9.3)

где А() и В() – вещественная и мнимая части соответственно.

Для рассматриваемого примера они рассчитываются по формулам:

А() = –1 + a₁²; B() = (–a₂ + a₀²). (9.4)

Подставим в выражения (9.4) значение частоты от минус до плюс бесконечности и построим кривую на комплексной плоскости см. рис. 9.1.

Н

Рис. 9.1. Область устойчивости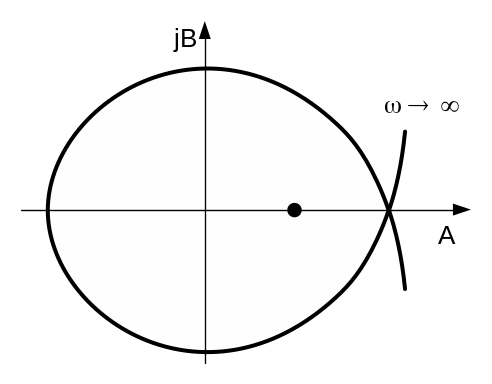

а полученную кривую наносим штриховку по следующему правилу: при движении по кривой от значений частоты лежащих в минус бесконечности, к значениям в плюс бесконечности, штриховка должна наноситься с левой стороны кривой.

Система будет устойчива при всех значениях коэффициента K, лежащих внутри заштрихованной области (штриховка внутрь области). Наибольшее значение коэффициента усиления будет соответствовать границе устойчивости САР.

В пояснительной записке курсового проекта, при выполнении данного пункта, должен присутствовать вывод исходных уравнений (подобных уравнениям (9.4)) и график кривой с указанными (штриховкой) областями устойчивости, а также вывод о попадании или нет коэффициента K в область устойчивости.