
- •Интегралы
- •Введение
- •Предисловие
- •Методические рекомендации
- •Теоретические вопросы
- •Теоретические упражнения
- •Расчетно-графические задания: I. Вычисление неопределенных интегралов; II, III, IV, V приложение определенного интеграла.
- •Вариант 28.
- •Вариант 29.
- •Вариант 30.
- •Оглавление
- •Интегралы
- •6 80021, Г. Хабаровск, ул. Серышева, 47
Теоретические упражнения
Какой из интегралов больше?
![]() или
или
![]()
Найти:

Найти точки экстремума функции
![]()
Доказать, что если f(х) – чётная функция, то
![]()
Доказать, что для нечётной функции f(х) справедливы равенства
![]() и
и
![]()
При каких целых значениях к интеграл
 выражается элементарными функциями?
выражается элементарными функциями?Вычислить интеграл
![]()
8. Применяя метод интегрирования по частям, получить рекуррентную формулу:
![]()
![]() 9.Вычислить,
исходя из определения, интеграл
9.Вычислить,
исходя из определения, интеграл
![]()
10. Исходя из геометрического значения определённого интеграла, доказать, что
а).
![]() б).
б).![]() в).
в).![]()
11. Найти ошибку, допущенную при следующем вычислении интеграла(интеграл от всюду положительной функции оказался равным нулю!)

![]() =0.
=0.
Расчетно-графические задания: I. Вычисление неопределенных интегралов; II, III, IV, V приложение определенного интеграла.
Вариант 1.
1.![]() 15.
15.![]() 28.
28.
![]()
2.![]() 16.
16.![]() 29.
29.
![]()
3.![]() 17.
17.
![]() 30.
30.
![]()
4.![]() 18.
18.
![]() 31.
31.
![]()
5.![]() 19.
19.
![]() 32.
32.
![]()
6.![]() 20.
20.
![]() 33.
33.
![]()
7.![]() 21.
21.
![]() 34.
34.
![]()
8.![]() 22.
22.
![]() 35.
35.
![]()
9.![]() 23.
23.
![]() 36.
36.
![]()
10.![]() 24.
24.
![]() 37.
37.
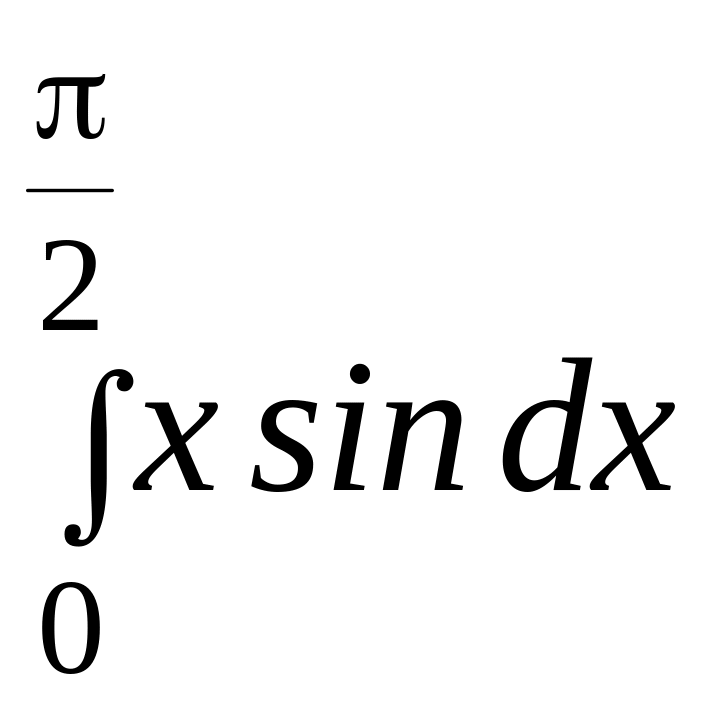
11.![]() 25.
25.
![]() 38.
38.
![]()
12.![]() 26.
26.
![]() 39.
39.
![]()
13.
![]() 27.
27.
![]() 40.
40.
![]()
14.![]()
Вариант 1.
II Вычислить площади:
а)
![]()
б)
![]()
в)
петли кривой
![]()
III. Вычислить длины дуг кривых:
а)
![]()
б)
![]() от
от
![]() до
до
![]()
в)
![]() от
от
![]() до
до
![]()
IV. Вычислить объемы тел, образованных вращением фигур, ограниченных линиями:
а)
![]()
![]()
![]()
б)
![]() вокруг оси Оу
вокруг оси Оу
в)
![]() (одной арки) вокруг
оси Ох
(одной арки) вокруг
оси Ох
V.
Окружность
![]() вращается вокруг
полярной оси. Определить площадь
поверхности вращения.
вращается вокруг
полярной оси. Определить площадь
поверхности вращения.
Вариант 2.
1.
![]() 15.
15.![]() 29.
29.
![]()
2.![]() 16.
16.![]() 30.
30.
![]()
3.![]() 17.
17.![]() 31.
31.
![]()
4.![]() 18.
18.
![]() 32.
32.
![]()
5.![]() 19.
19.
![]() 33.
33.
![]()
6.![]() 20.
20.
![]() 34.
34.
![]()
7.![]() 21.
21.
![]() 35.
35.
![]()
8.![]() 22.
22.
![]() 36.
36.
![]()
9.![]() 23.
23.
![]() 37.
37.

10.![]() 24.
24.
![]() 38.
38.![]()
11.![]() 25.
25.
![]() 39.
39.
![]()
12.![]() 26.
26.
![]() 40.
40.
![]()
13.![]() 27.
27.
![]()
14.![]() 28.
28.
![]()
Вариант 2.
II. Вычислить площади фигур ограниченных линиями
а)
![]() ;
;
![]()
б)
площадь фигуры, лежащей вне круга
![]() и ограниченной кривой
и ограниченной кривой
![]()
в)
![]()
III. Вычислить длины дуг кривых:
а)
![]() между точками
между точками
![]()
![]()
б)
![]() от
от
![]() до
до
![]()
в)
![]()
IV. Вычислить объемы тел, образованных вращением фигур, ограниченных линиями:
а)
![]() вокруг оси Ох
вокруг оси Ох
б)
![]() вокруг оси Оу
вокруг оси Оу
в)
![]() вокруг оси Ох (одной арки)
вокруг оси Ох (одной арки)
V.
Найти площадь поверхности, образованной
вращением вокруг оси Оу петли кривой:
![]()
Вариант 3.
1.![]() 15.
15.![]() 28.
28.
![]()
2.![]() 16.
16.![]() 29.
29.
![]()
3.![]() 17.
17.![]() 30.
30.
![]()
4.![]() 18.
18.
![]() 31.
31.
![]()
5.![]() 19.
19.
![]() 32.
32.
![]()
6.![]() 20.
20.
![]() 33.
33.
![]()
7.![]() 21.
21.
![]() 34.
34.
![]()
8.![]() 22.
22.
![]() 35.
35.
![]()
9.![]() 23.
23.
![]() 36.
36.
![]()
10.![]() 24.
24.
![]() 37.
37.
![]()
11.![]() 25.
25.
![]() 38.
38.
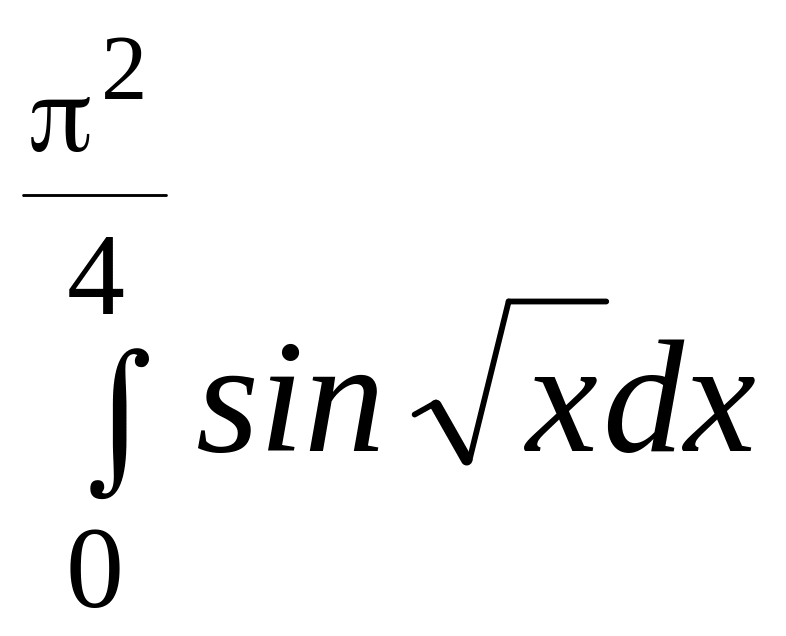
12.![]() 26.
26.
![]() 39.
39.
![]()
13.![]() 27.
27.
![]() 40.
40.
![]()
14.![]()
Вариант 3.
II. Вычислить площади фигур, ограниченных линиями:
а)
![]()
б)
![]() и
и
![]()
в)
![]() и осью Ох (одной арки)
и осью Ох (одной арки)
III. Вычислить длины дуг кривых:
а)
![]() ,
заключенный между точками с абсциссами
,
заключенный между точками с абсциссами
![]()
б)
петли кривой
![]()
в)
![]()
IV. Вычислить объемы тел, образованных вращением фигур, ограниченных линиями:
а)
![]() вокруг оси Ох
вокруг оси Ох
б)
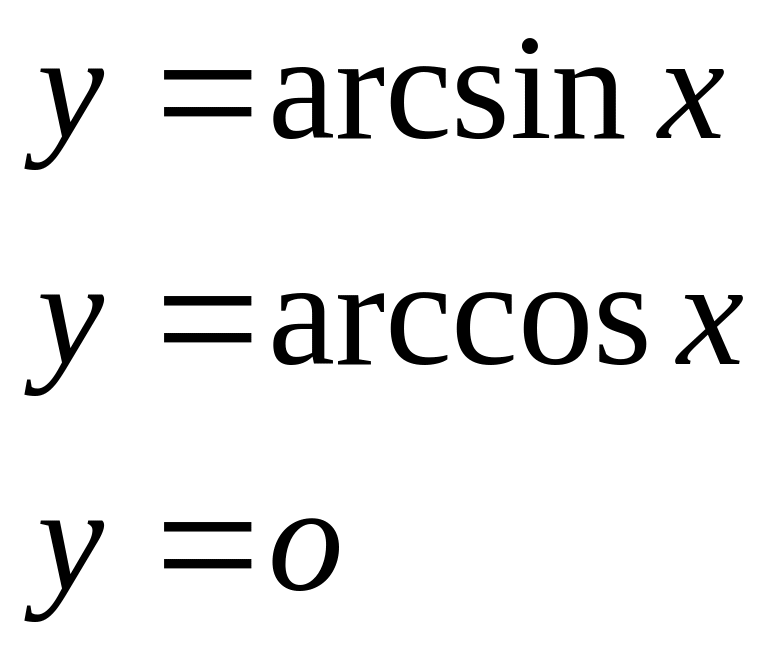 вокруг оси Оу
вокруг оси Оу
в)
![]()
![]() вокруг оси Ох
вокруг оси Ох
V.
Найти площадь поверхности, образованной
вращением кривой
![]() ,
заключенной между прямыми
,
заключенной между прямыми
![]() вокруг оси Ох.
вокруг оси Ох.
Вариант 4.



Вариант 4.
II. Вычислить площади фигур, ограниченных линиями:
а)
![]()
б)
![]() и
и
в)
![]()
III. Вычислить длины дуг кривых:
а)
![]() ,
заключенной между точками с координатами
,
заключенной между точками с координатами
![]()
б)
![]() от
от
![]()
в)
![]() от
от
![]() до
до
IV. Вычислить объемы тел, образованных вращения фигур, ограниченных линиями:
а)
![]() ;
;
![]() ;
;
![]() вокруг оси Ох
вокруг оси Ох
б)
![]() ;
;
![]() ;
;
![]() вокруг оси Оу
вокруг оси Оу
в)
![]() вокруг оси Ох
вокруг оси Ох
V. Определить площадь поверхности, образованной вращением кривой
![]() вокруг
оси Ох.
вокруг
оси Ох.
Вариант 5.

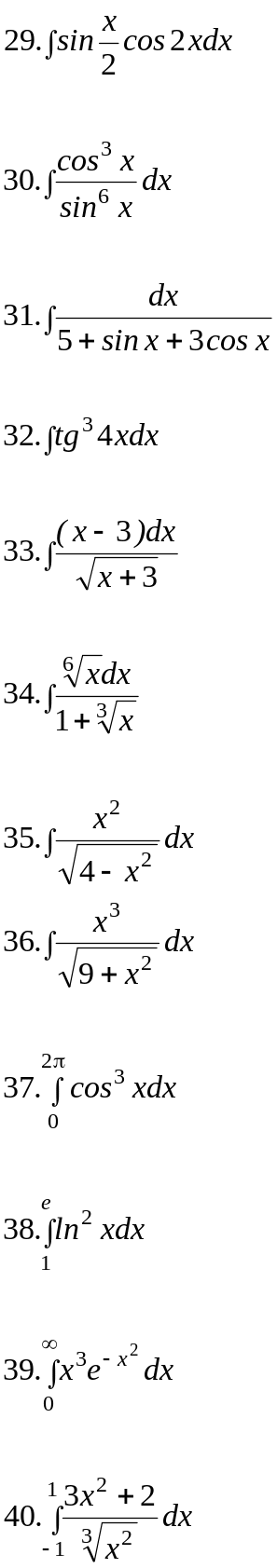
Вариант 5.
II. Вычислить площади фигур, ограниченных линиями
а)
![]() ;
;
![]()
б)
части
![]() лежащей внутри окружности
лежащей внутри окружности
![]()
в)
![]()
![]()
III. Вычислить длины дуг кривых:
а)
периметр фигуры, ограниченной линиями:
![]() ;
;
![]()
б)
![]()
![]()
в)
![]()
IV. Вычислить объемы тел, образованных вращением фигур, ограниченные линиями:
а)
![]() ;
вокруг оси Ох
;
вокруг оси Ох
б)
![]() ;
;
вокруг оси Оу
;
;
вокруг оси Оу
в)
![]() вокруг оси Ох (одной арки)
вокруг оси Ох (одной арки)
V. Определить площадь поверхности, образованной вращением кривой
![]() вокруг
оси Оу.
вокруг
оси Оу.
Вариант 6.

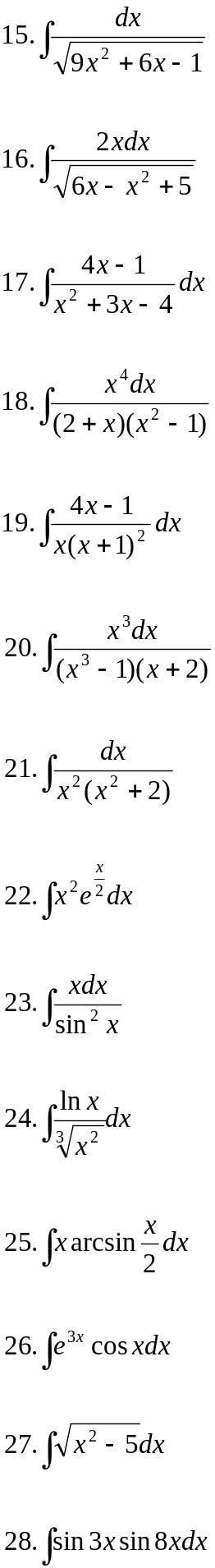

Вариант 6.
II. Вычислить площади фигур, ограниченных линиями
а)
![]() ;
;
![]() ;
;
б)
![]()
![]()
в)
петли кривой
![]()
III. Вычислить длины дуг кривых:
а)
![]() , отсеченной осью Ох
, отсеченной осью Ох
б)
![]()
![]()
в)
![]()
IV. Вычислить объемы тел, образованных вращением фигур, ограниченные линиями:
а)
![]() ;
;
;
;
![]() ;
;
![]() вокруг оси Ох
вокруг оси Ох
б)
![]() ;
;
;
;
;
;
![]() ;
вокруг оси Оу
;
вокруг оси Оу
в)
![]() вокруг оси Оу
вокруг оси Оу
V.
Вычислить площадь поверхности,
образованной вращением вокруг оси Ох
кривой
![]() отсеченной прямой
отсеченной прямой
![]()
Вариант 7.



Вариант 7.
II. Вычислить площади фигур, ограниченных линиями
а)
;
![]()
б)
части
![]() лежащей внутри
лежащей внутри
![]()
в)
петли кривой
![]()
III. Вычислить длины дуг кривых:
а)
периметр фигур, состоящих из дуг кривых
![]() и
и
![]()
б)
от
до
![]()
в)
![]()
IV. Вычислить объемы тел, образованных вращением фигур, ограниченные линиями:
а)
![]() ;
;
![]() ;
вокруг оси Ох
;
вокруг оси Ох
б)
![]() ;
;
вокруг оси Оу
;
;
вокруг оси Оу
в)
от
до
![]() ,
вокруг оси Ох
,
вокруг оси Ох
V. Вычислить площадь поверхности, образованной вращением кривой
![]() вокруг
оси Ох от
до
вокруг
оси Ох от
до
![]()
Вариант 8.


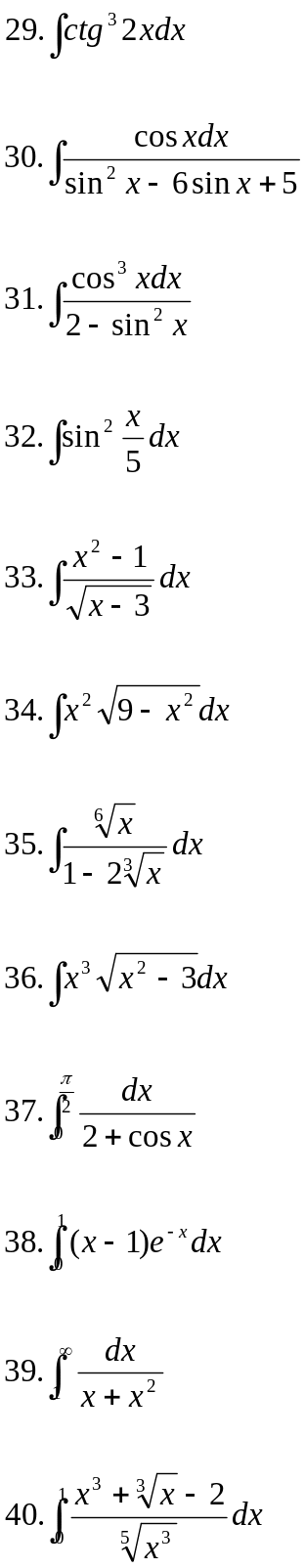
Вариант 8.
II.Вычислить площадь фигур, ограниченных линиями:
a)![]() ;y=
;y=![]()
б)![]() (перейти к полярным координатам)
(перейти к полярным координатам)
в)
петли кривой
![]()
III. Вычислить длины дуг кривых.
a)
y=ln sin x
![]()
б)
![]() от
t=0 до
t =
от
t=0 до
t =![]()
в)
=1
от =![]() до =
до =![]()
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a)
x
=
![]() x
= 1 y
= 1 вокруг оси Ох
x
= 1 y
= 1 вокруг оси Ох
б)
у = arccos
![]() вокруг оси Оу, у = 0, y
= arccos
x
вокруг оси Оу, у = 0, y
= arccos
x
в)
![]() вокруг оси Оу
вокруг оси Оу
V. Вычислить площадь поверхности, образованной вращением кривой
![]() вокруг
оси Ох.
вокруг
оси Ох.
Вариант 9.
|
|
|
Вариант 9.
II.Вычислить площадь фигур, ограниченных линиями:
a)
х=у![]() ,
х=
,
х=![]()
б) a sin 3
в)
![]()
III. Вычислить длину дуг кривых.
a) y=ln(2cosx) между точками пересечения с осями координат
б)
![]() от t=0
до t=
от t=0
до t=
в)
![]()
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a) y=4x – x y=x вокруг оси Ох
б)
у=![]() вокруг оси оу х=0, у=0
вокруг оси оу х=0, у=0
в)
t=0
t=![]() вокруг оси Ох
вокруг оси Ох
V. Найти площадь поверхности, образованной вращением вокруг оси ох кривой
![]() между
точками пересечения с осями координат
между
точками пересечения с осями координат
Вариант 10.
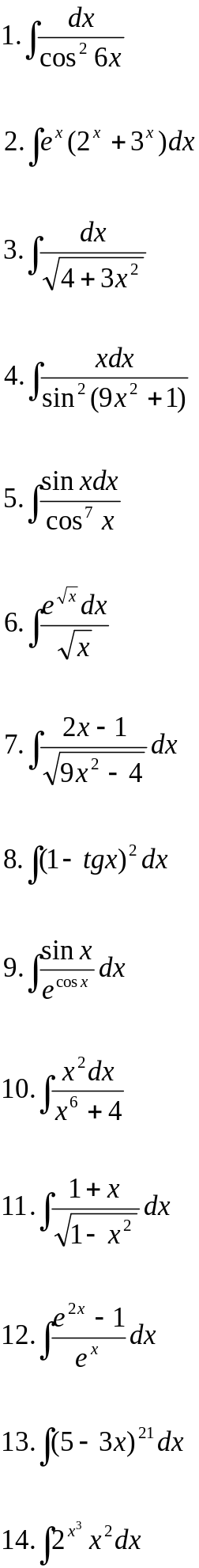
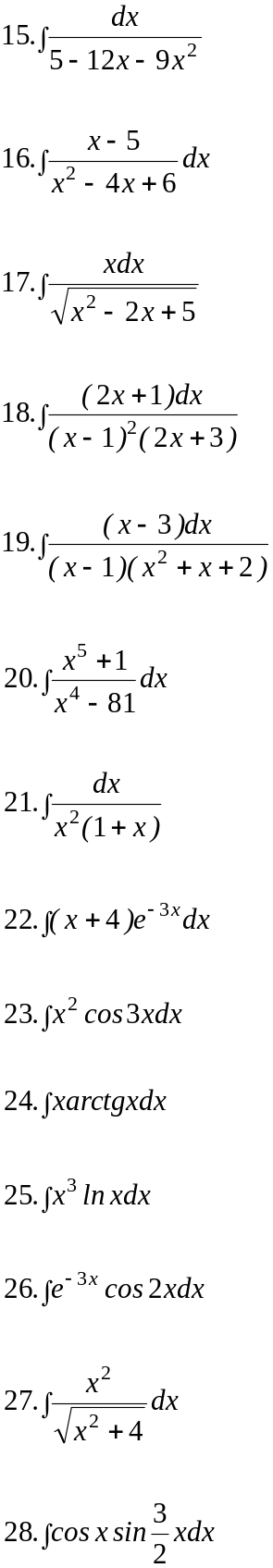

Вариант 10.
II.Вычислить площадь фигур, ограниченных линиями:
a)
y=x
+1
; y=![]() x
;
y=5.
x
;
y=5.
б) p=a(1-cos ) вне кривой p=a cos
в)
![]()
III. Вычислить длину дуг кривых.
a)
y=arcsin
e![]() от x=0
до x=1
от x=0
до x=1
б) от t=0 до t=
в)
p=a
sec
(-![]() )
от =0
до =
)
от =0
до =![]()
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a) y=ln x , x=e , y=0 вокруг оси Оx
б) y=x 8x=y вокруг оси Оу
в)
![]() (одной арки) вокруг оси Оу
(одной арки) вокруг оси Оу
V.Вычислить площадь поверхности, образованной вращением петли кривой
![]() вокруг
оси Ох.
вокруг
оси Ох.
Вариант 11.

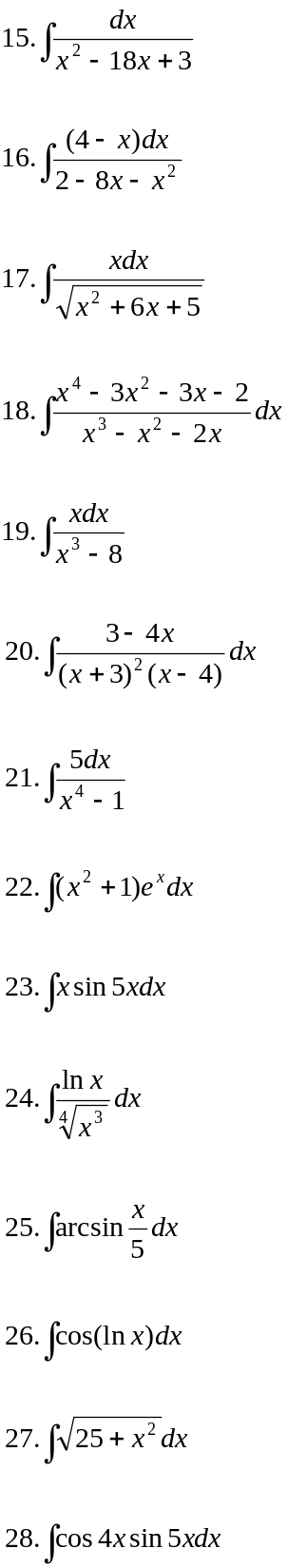

Вариант 11.
II.Вычислить площадь фигур, ограниченных линиями:
a)![]() ;
y
-24x=48
;
y
-24x=48
б) 2-cos3 (между смежными наибольшим и наименьшим радиусами кривой)
в)
![]() осью Оу
осью Оу
III. Вычислить длину дуг кривых.
a)
y=![]() между прямыми х= а
между прямыми х= а
б)![]()
в)
2е![]()
![]()
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a)
y=sinx
y=![]() x
вокруг оси Ох
x
вокруг оси Ох
б)
![]() у= 1
вокруг оси Оу
у= 1
вокруг оси Оу
в)
![]() вокруг оси Оу
вокруг оси Оу
V.Вычислить площадь поверхности, образованной вращением кривой вокруг оси ох кардиоиды.
Х= 2(2cos t-cos2t)
Y=2(2sint-sin2t)
Вариант 12.



Вариант 12.
II. Вычислить площадь фигур, ограниченных линиями:
a)![]() ;
x
+y
=8
;
x
+y
=8
б) a sin 3
в)
III. Вычислить длину дуг кривых.
a) петли 9ay = x(x-3a)
б)
![]() от
t=0
до t
=
от
t=0
до t
=
в)
=![]() от =
от =![]() до =
до =
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a) y= x=-a x=a y=0 вокруг оси Ох
б)
y=x![]() ,
y=0,
x=2
вокруг оси Оу
,
y=0,
x=2
вокруг оси Оу
в) осью Оу, вокруг оси Оу
V. Вычислить площадь поверхности, образованной вращением вокруг оси ох кривой
![]() (перейти
к полярным координатам)
(перейти
к полярным координатам)
Вариант 13.



Вариант 13.
II.Вычислить площадь фигур, ограниченных линиями:
a) y=0 ; y=(x+1) ; y=4-x
б) p=2+cos
в) 0< t<
III. Вычислить длины дуг кривых.
a) y=ln(1-x ) от x=- до x=
б)![]() от t=
до t=
от t=
до t=![]()
в)
p=12e![]() от =0
до =
от =0
до =
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a) y=x +1 ; y=3x-1 вокруг оси Оx
б) (x-1) +y =1 вокруг оси Оy
в)
![]() петли кривой вокруг Ох
петли кривой вокруг Ох
V.Вычислить площадь поверхности, образованной вращением одной арки циклоиды вокруг оси оу.
![]()
Вариант 14.


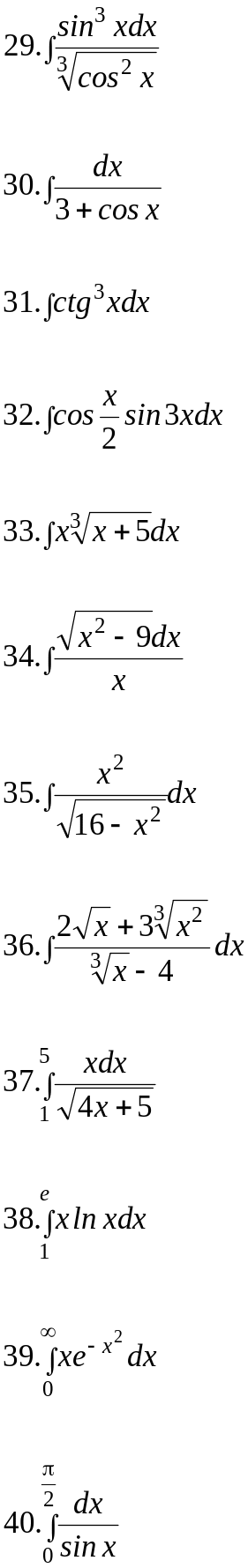
Вариант 14.
II.Вычислить площадь фигур, ограниченных линиями:
a) y=x ; y=8-x
б) p=2+sin3 между смежными наибольшим и наименьшим радиусами кривой
в)
петли кривой
![]()
III. Вычислить длину дуг кривых.
a) y=ln(2cosx) между точками пересечения с осями координат
б)
![]() от t=0
до t=
от t=0
до t=
в) p=6(1+sin )
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a)
y=![]() вокруг её асимптоты
вокруг её асимптоты
б) y=x(4-x) y=0 вокруг оси Оу
в)
![]() (одной арки) вокруг оси Оу
(одной арки) вокруг оси Оу
V. Определить площадь поверхности, образованной вращением вокруг оси Ох дуги
между точками пересечения с осями координат.
Вариант 15.

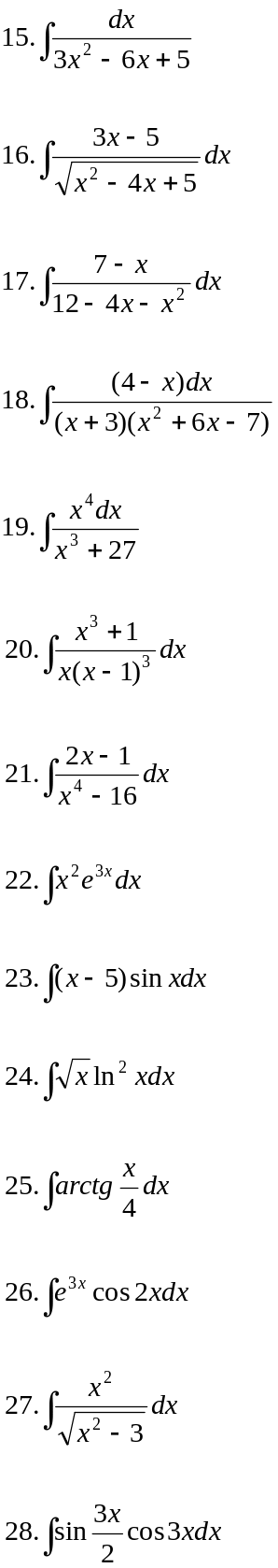

Вариант 15.
II.Вычислить площадь фигур, ограниченных линиями:
a)
![]() +
+![]() =1
и
x+y=1
=1
и
x+y=1
б)
p=2![]() a
cos
и
p=2a sin
a
cos
и
p=2a sin
в)
петли кривой
![]()
III. Вычислить длину дуг кривых.
a) y=2 от x=1 до x=4
б)
![]()
в) p=5(1-cos ) от =- до =0
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a) y=4x – x y=x вокруг оси Ох
б)
y=e![]() ;
x=0
, x=2
вокруг оси Оу, y=0;
;
x=0
, x=2
вокруг оси Оу, y=0;
в)
![]() осями х=0 , у=0 вокруг оси Ох
осями х=0 , у=0 вокруг оси Ох
V.Вычислить площадь поверхности, образованной вращением дуги кривой
вокруг оси ох от t=0 до t=
Вариант 16.

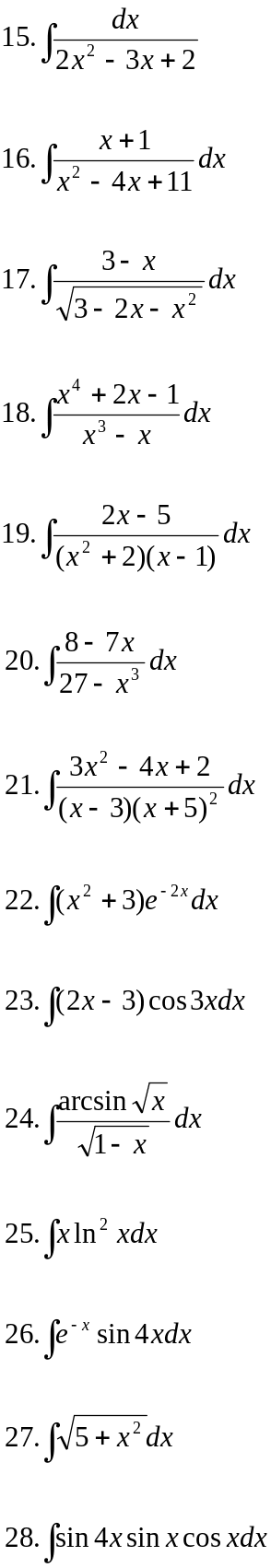
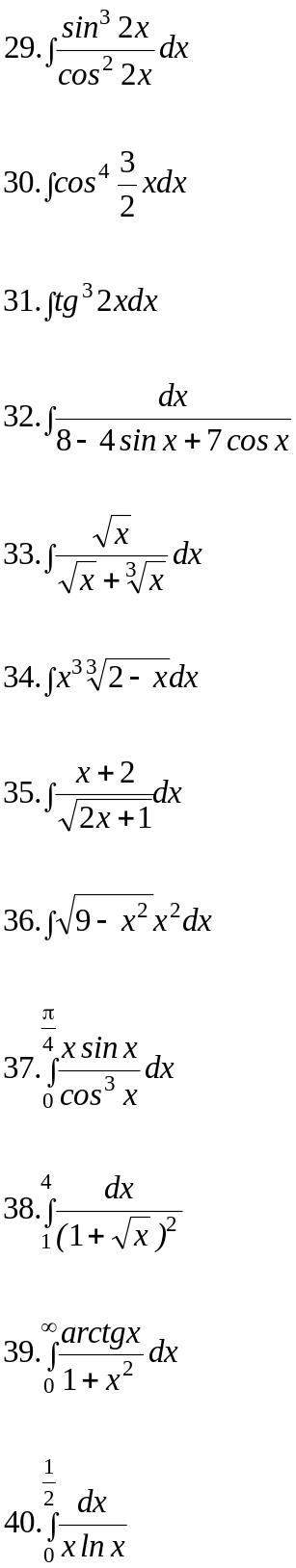
Вариант 16.
II.Вычислить площадь фигур, ограниченных линиями:
a)
x=y
;
x=![]()
б)
(![]() перейти к полярным координатам
перейти к полярным координатам
в)
![]()
III. Вычислить длину дуг кривых.
a)
y![]() ;
x=4
(периметр фигуры)
;
x=4
(периметр фигуры)
б) от t=0, t=
в) p=8(1+cos )
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a)
x![]() y
y![]() вокруг оси Ох
вокруг оси Ох
б) у=2x-x ; y=0 вокруг оси оу
в) от t=0, t= , вокруг оси Ох
V.Вычислить площадь поверхности, образованной вращением дуги кривой вокруг оси ох.
y![]()
![]()
Вариант 17.



Вариант 17.
II.Вычислить площадь фигур, ограниченных линиями:
a) y=(x-4) ; y=16-x вокруг оси Ох
б) x=a(cos t+t sin t) от t=0 до t=
y=a(sin t-t cos t)
в) p=8sin
III. Вычислить длину дуг кривых.
a)
![]() =2px,
отсеченной прямой х=
=2px,
отсеченной прямой х=![]()
б) x=a(cos t-t sin t)
y=a(sin t-t cos t) от t=0 до t=
в) p=8sin
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a) y=(x-4) , y=16-x вокруг оси Ох
б) y=sin x , x=0 , y=1 вокруг оси Оу
в)
![]() между точками пересечения с осью ох
вокруг оси ох
между точками пересечения с осью ох
вокруг оси ох
V.Вычислить
площадь поверхности, образованной
вращением кривой x=![]() вокруг оси Оy от y=1
до y=e.
вокруг оси Оy от y=1
до y=e.
Вариант 18.



Вариант 18.
II.Вычислить площадь фигур, ограниченных линиями:
a)
y=4x
y=![]() y=2
y=2
б)
=a![]() =acos
вне
кардиоиды
=acos
вне
кардиоиды
в)
Второй аркой циклоиды
![]() и осью Ох
и осью Ох
III. Вычислить длину дуг кривых.
a)
периметр фигуры x![]() ,y=1
,y=1
б)
![]() между точками пересечения с осями
координат
между точками пересечения с осями
координат
в)
=2![]()
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a)
![]() х=-3 вокруг оси Ох
х=-3 вокруг оси Ох
б) у=cosx y=0 x=0 вокруг оси Оу
в)
![]() осями координат, вокруг оси Ох
осями координат, вокруг оси Ох
V.Вычислить площадь поверхности, образованной вращением кривой
Y=x вокруг оси оx от точки 0(0;0) до точки М(1,1)
Вариант 19.


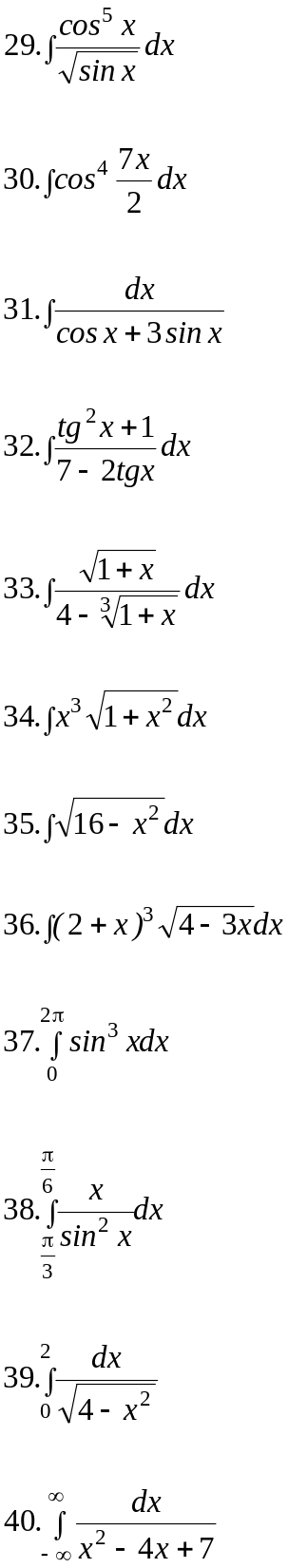
Вариант 19.
II.Вычислить площадь фигур, ограниченных линиями:
a) y=x -2x+2, касательной к ней в т.(3;5 ) и осью ординат
б)
=а![]() =а
=а
в)
![]() и осью Оу
и осью Оу
III. Вычислить длину дуг кривых.
a)
у![]() отсечённой прямой х =-1
отсечённой прямой х =-1
б)![]() 0
0![]()
в)
=3e![]() от=0
до=
от=0
до=![]()
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a) y=4-x и 2х+у-4=0 вокруг оси Оу
б) у=х и 8х=у вокруг оси Оу
в) петли кривой вокруг оси Ох
V.Вычислить площадь поверхности, образованной вращением кривой
х![]() вокруг оси Оу.
вокруг оси Оу.
Вариант 20.
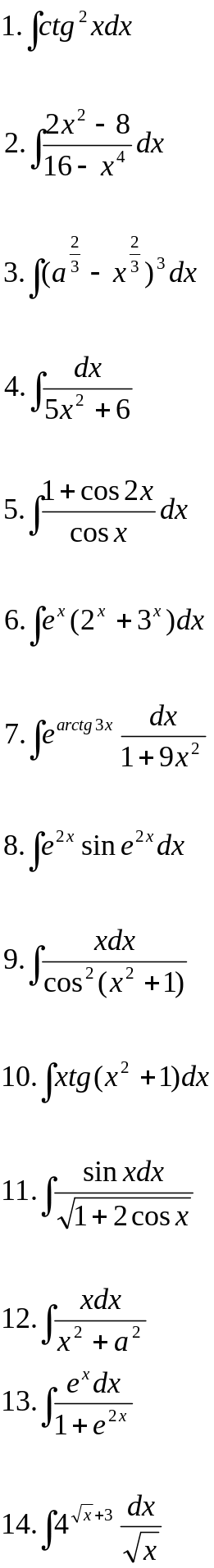

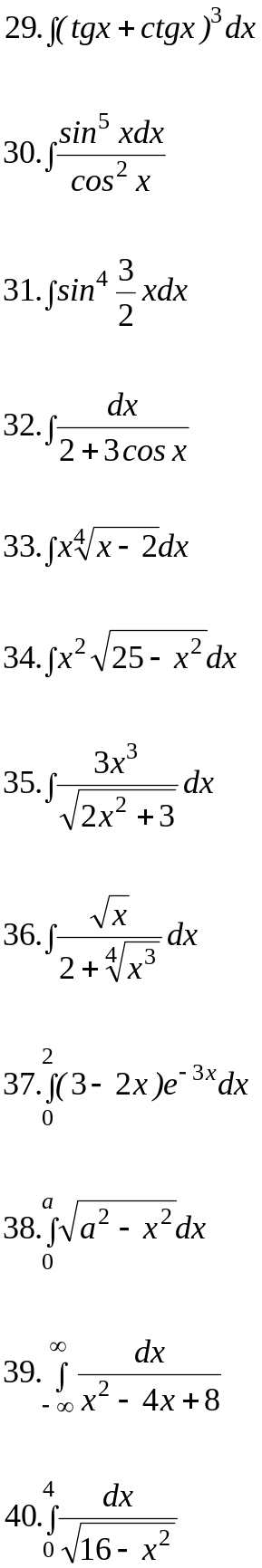
Вариант 20.
II.Вычислить площадь фигур, ограниченных линиями:
a) Найти площадь между параболой у=-х -2х+3, касательной к ней в точке М (2;5) и осью ординат
б) аsin2 , а (вне первой кривой )
в)![]() от 0 до2
от 0 до2
III. Вычислить длину дуг кривых.
a) y=eх между точками (0;1); (1;е)
б)
![]() 0
0![]()
в) =9cos
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a)
x![]() +y
=a
x=0
y=0
вокруг оси Ох
+y
=a
x=0
y=0
вокруг оси Ох
б)
у=![]() вокруг оси оу х=0, у=0
вокруг оси оу х=0, у=0
в)
![]() осью оу, вокруг оси Оу
осью оу, вокруг оси Оу
V.Вычислить площадь поверхности, образованной вращением одной арки циклоиды
![]()
вокруг оси Ох.
Вариант 21.

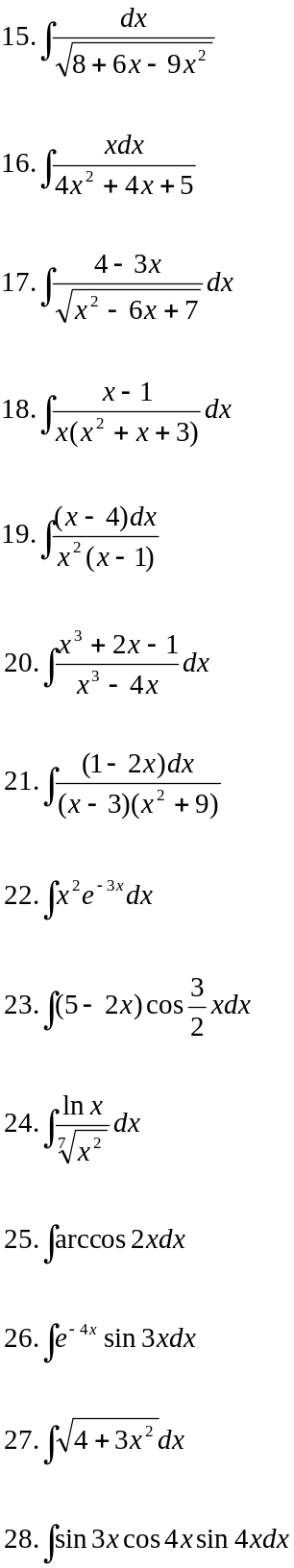

Вариант 21.
II.Вычислить площадь фигур, ограниченных линиями:
a) y=(x+1) y=cosx y=0
б) =2a(1-cos)
в)
![]() и осями координат
и осями координат
III. Вычислить длину дуг кривых.
a)
3у![]() между точками пересечения с осью Ох
между точками пересечения с осью Ох
б)
![]() от t=0
до t=
от t=0
до t=
в)
e![]() от
от
![]()
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a)
2х-х![]() 2х
2х![]() вокруг оси Ох
вокруг оси Ох
б) ху=9 у=3 у=9 х=0 вокруг Оу
в)
![]() от t=0
t=6
вокруг оси Ох
от t=0
t=6
вокруг оси Ох
V.Вычислить
площадь поверхности, образованной
вращением вокруг оси Ох кривой 8у![]() .
.
Вариант 22.
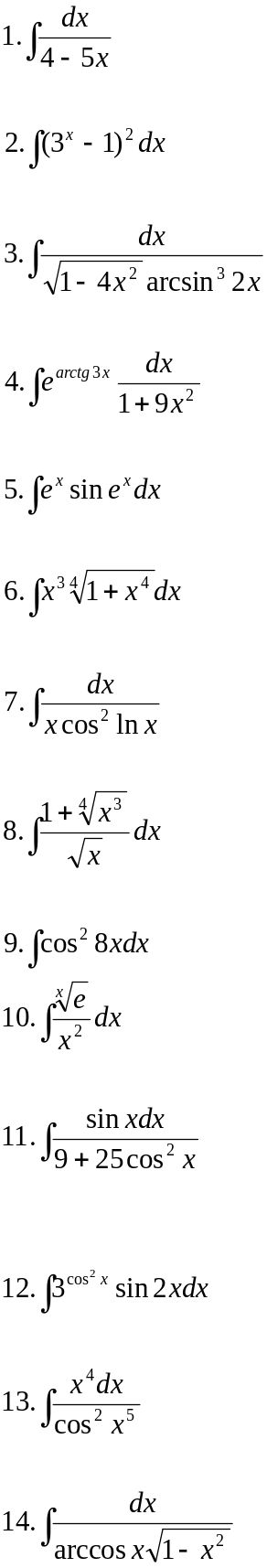
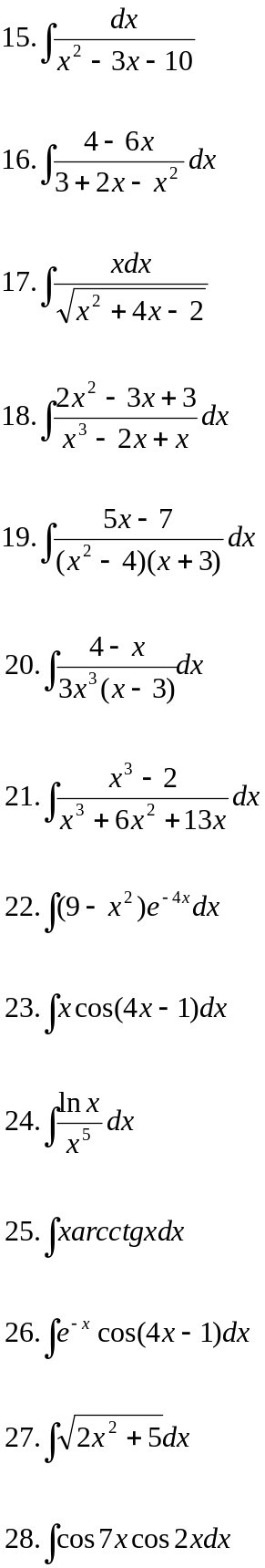

Вариант 22.
II.Вычислить площадь фигур, ограниченных линиями:
a) у =4х , х =4у, х +у =5
б)
а
вне кривой
![]()
в)
![]() и осью оу
и осью оу
III. Вычислить длину дуг кривых.
a)
у=ln
(cos
x)
+ 2 (0![]() )
)
б)
![]() между точками пересечения с осью Ох
между точками пересечения с осью Ох
в) a(sin+cos)
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a)
у=0,25х![]() и 5х-8у+14=0 вокруг оси Ох
и 5х-8у+14=0 вокруг оси Ох
б) у=lnx, x=2 y=0 вокруг оси Оу
в)
![]() прямыми у=0, у=2 вокруг оси Оу
прямыми у=0, у=2 вокруг оси Оу
V.Вычислить площадь поверхности, образованной вращением вокруг оси Оу кривой.
![]() .
.
Вариант 23.



Вариант 23.
II.Вычислить площадь фигур, ограниченных линиями:
a)
х
=4у
![]()
б)![]() у=4 (у
у=4 (у![]() 4)
4)
в) =а(1+sin) вне кривой =аsin
III. Вычислить длину дуг кривых.
a)
y=![]() 0
0![]()
б) 4(1+cos)
в) петли кривой
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a) у=х +3, х=4, х=0 у=0 вокруг оси Оу
б) у =(4+х) х=0 вокруг оси Ох
в) и осью Оу (одной арки циклоиды)
V. Вычислить площадь поверхности вращения фигуры, ограниченной линией
![]() ,
вокруг оси Ox.
,
вокруг оси Ox.
Вариант 24.

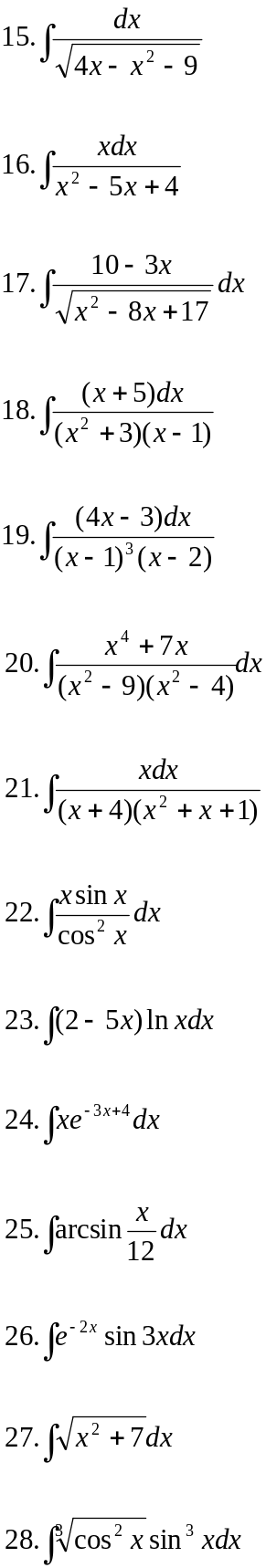
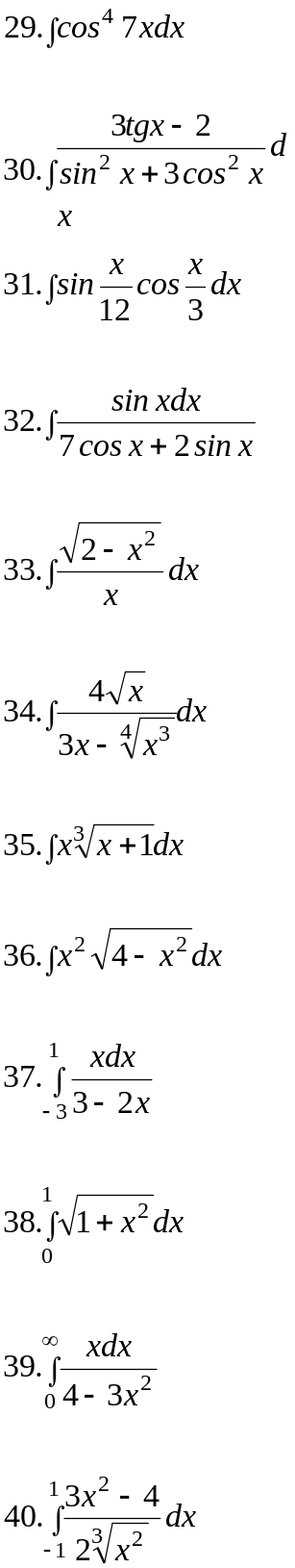
Вариант 24.
II.Вычислить площадь фигур, ограниченных линиями:
a) х=-2у х=1-3у
б) =2asin3 вне круга а
в)
![]() и прямой у=4 (у
и прямой у=4 (у![]() )
)
III. Вычислить длину дуг кривых.
a)
у=2-е
(ln![]() )
)
б)
![]()
в) от до
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a) у=10-х2 , у=х +2, х=0 вокруг оси Оу
б) у=хе , х=1, у=0 вокруг оси Ох
в)
![]()
V. Вычислить площадь поверхности, образованной вращением петли кривой 9х =у(3-у) вокруг оси Оу.
Вариант 25.
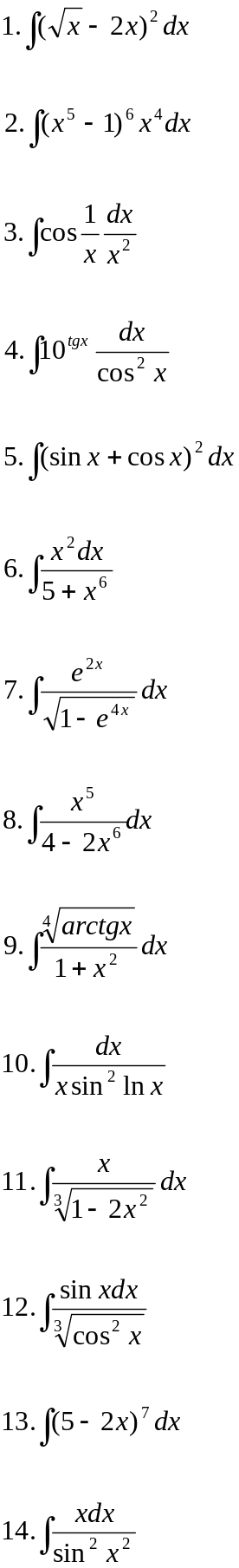

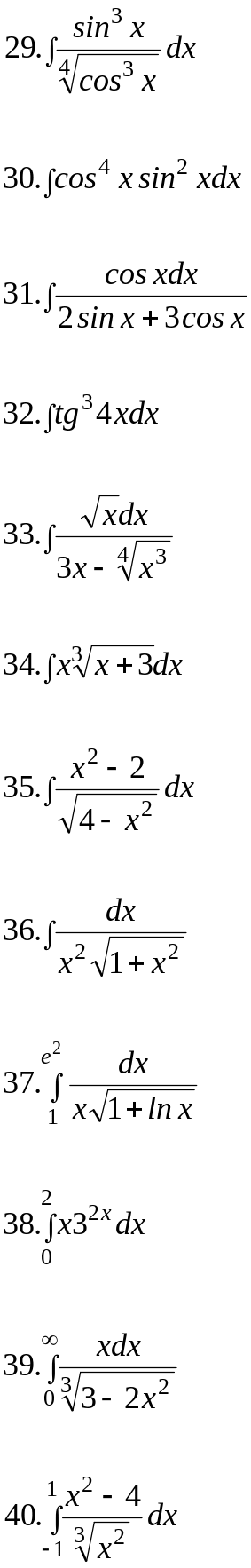
Вариант 25.
II.Вычислить площадь фигур, ограниченных линиями:
a) у=(х-1) у=cosx y=0
б) a(1-cos) a
в)
![]() и осями координат (I
четверть)
и осями координат (I
четверть)
III. Вычислить длину дуг кривых.
a) 3у =х(х-1) между точками пересечения с осью Ох
б)![]() от t
=0 до t=2
от t
=0 до t=2
в)e![]() от =0
до =
от =0
до =
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a) 2х+х -у=0 вокруг оси Ох
-2х -4х+у=0
б) ху=18, у=3, у=9, х=0
вокруг оси Оу
в)
![]() (t=0
до t=8)
вокруг оси Ох
(t=0
до t=8)
вокруг оси Ох
V.Найти площадь поверхности, образованной вращением вокруг оси Ох кривой
между точками пересечения с осями координат.
Вариант 26.

13.
![]()
14.![]()
![]()


Вариант 26.
II.Вычислить площадь фигур, ограниченных линиями:
a) х=-2у х=1-3у
б)
3a
sin
![]()
в)
![]() 0
0
III. Вычислить длину дуг кривых.
a)
y=ln
(cos
x),
заключённой между точками с абсциссами
х=0, х=![]()
б) от t=0 до t=2
в)
asin![]()
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a) y=x -2x+1 x=2 y=0 вокруг оси Оу
б)
у=е![]() у=0, х=0, х=1 вокруг оси Ох
у=0, х=0, х=1 вокруг оси Ох
в)
![]() вокруг Оу.
вокруг Оу.
V. Вычислить площадь поверхности, образованной вращением кривой у +4ух=2lny вокруг оси Оу от у=1 до у=2.
Вариант 27.
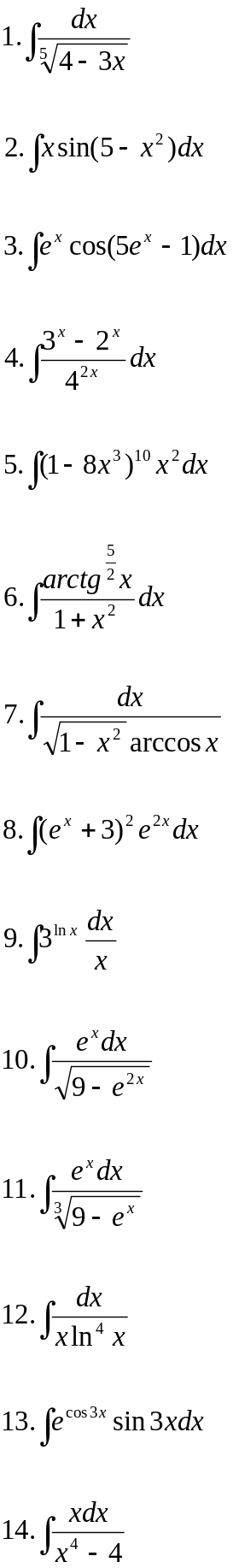
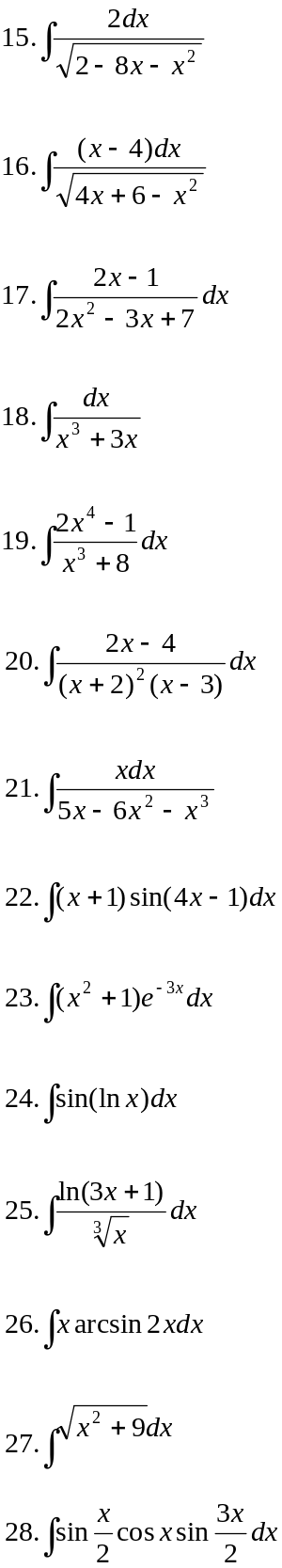
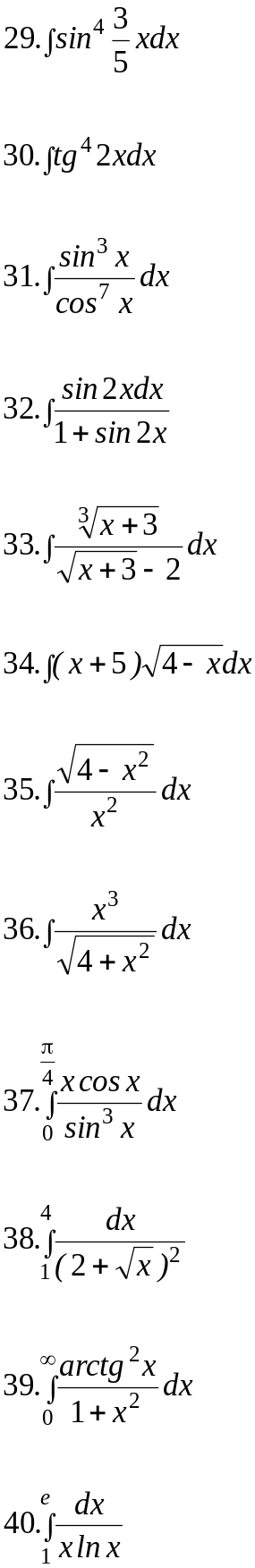
Вариант 27.
II.Вычислить площадь фигур, ограниченных линиями:
a) у=2х-х , у+х=0
б) (1+cos ) и
в)
![]() и осями координат
и осями координат
III. Вычислить длину дуг кривых.
a)
у
=х
отсечённой прямой![]()
б) между
точками пересечения с осями координат
между
точками пересечения с осями координат
в)аsin
IV.Вычислить объёмы тел, образованных вращением фигур, ограниченных линиями
a) y=cos(x- ) ,.х=0, у=0 (при х0) вокруг оси Ох
б) у=х х=0, у=8 вокруг оси Оу
в)
одной арки циклоиды вокруг оси Ох
![]()
V. Вычислить площадь поверхности, образованной вращением дуги кривой у =4+х, отсечённой прямой х=2 вокруг оси Ох.

