41. Сетчатые своды Песельника. Узлы. Основы расчета.
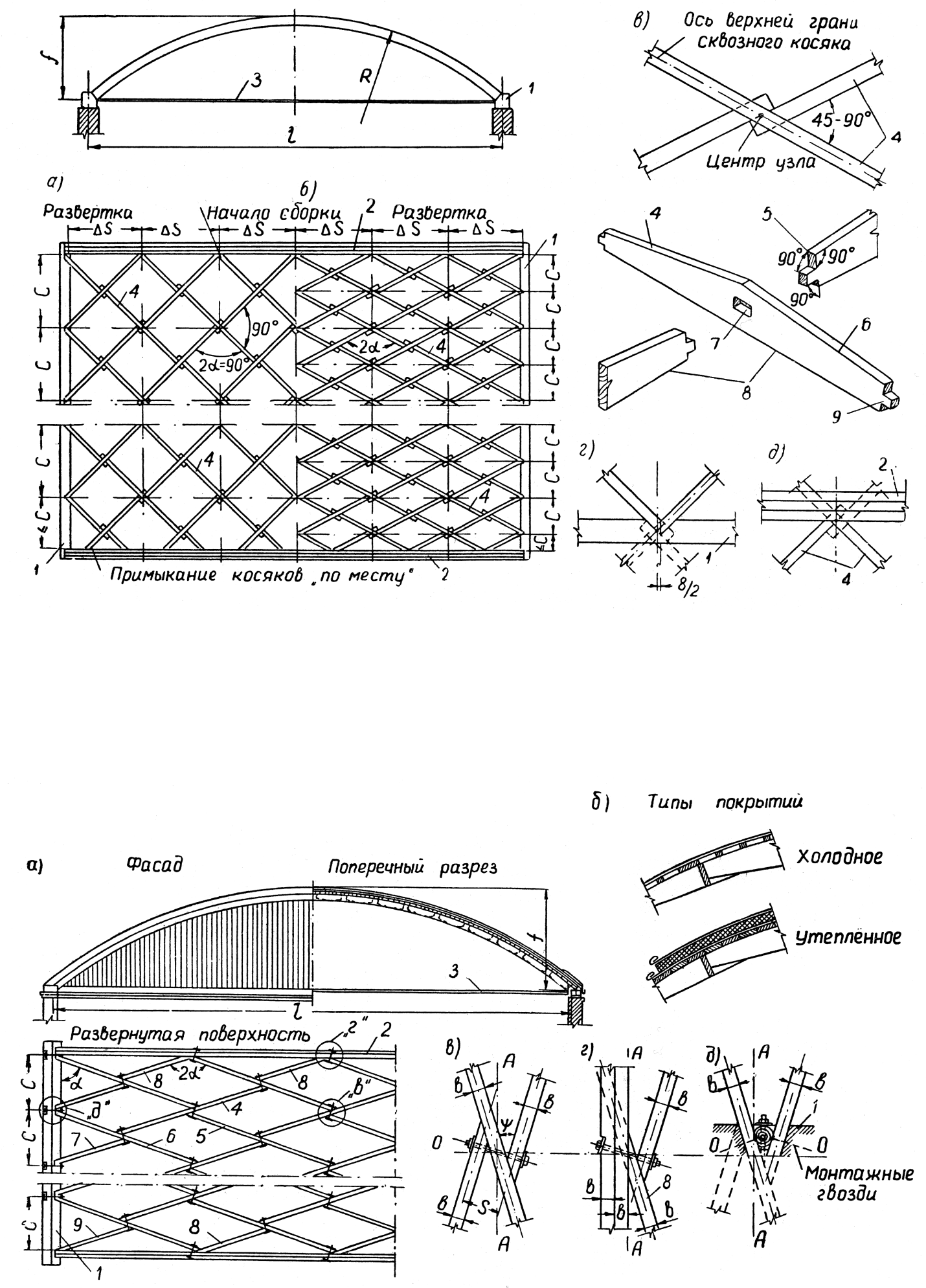
Ввиду несовпадения плоскости действия расчетного момента для арки М0 и нормальной силы N0 с осью косяка, наклоненного к образующей свода под углом а, расчетный изгибающий момент для сквозного косяка
(8.1)
и нормальная сила для косяка
(8.2)
Расчет ведется с учетом совместного действия сжатия и изгиба. Гибкость свода с учетом пространственной работы его определяется по общей формуле с введением эмпирического коэффициента 0,7. Расчетная длина с учетом косого направления косяков увеличивается делением на sinα. Тогда
(8.3)
Для безметалльных сводов системы С. И. Песельника гибкость на основании ряда испытаний таких сводов рекомендуется принимать
(8.4)
где l0 — расчетная длина дуги свода, которая принимается при симметричной нагрузке для двухшарнирной арки l0 = 0,6S и для трехшарнирной арки l0 = 0,7S; при односторонней нагрузке в обоих случаях принимается l0 = 0,5S;
S — длина дуги свода.
Проверка напряжений в косяке производится по формуле:
(8.5)
или подставив значения Мк и Wк из формул (26.1) и (26.2), получим
где Fнт и Wнт — соответственно площадь и момент сопротивления нетто поперечного сечения косяка в середине его длины.
При малых значениях второго слагаемого, т. е. когда напряжение изгиба не превосходит 10% от напряжения сжатия косяка, ими следует пренебречь и ввести в знаменатель первого слагаемого коэффициент продольного изгиба φ, определяемый по расчетной гибкости λ.
Внецентренное примыкание к сквозному косяку двух набегающих косяков создает в нем изгибающий момент в другой плоскости, который предполагается погашенным настилом и при расчете обычно не учитывается.
42. Сетчатые своды их конструктивные решения узлов и основы расчета.
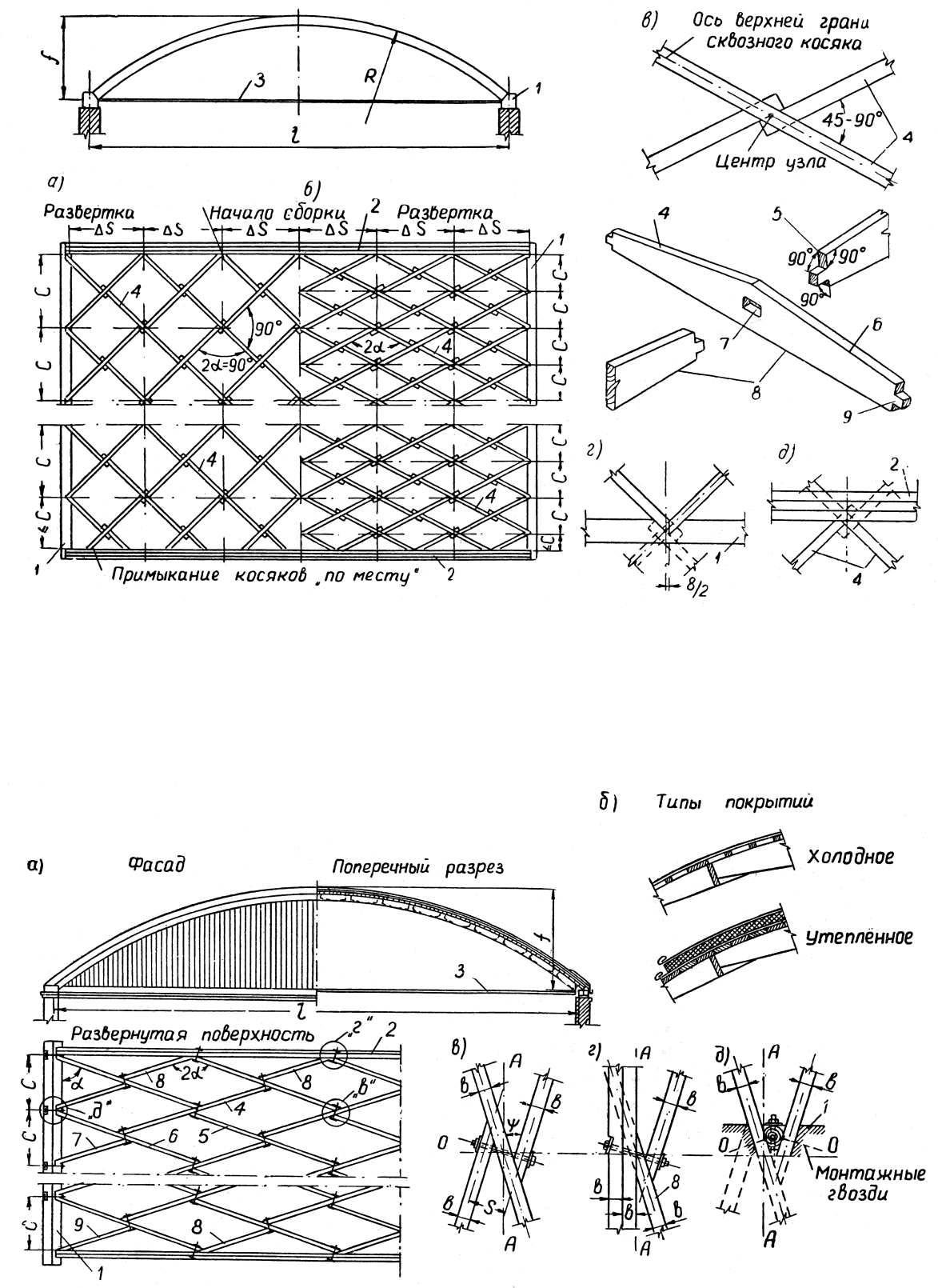
Для расчета сетчатого свода выделяют расчетную полосу свода шириной, соответствующей шагу косяков вдоль образующей (МАУЭРЛАТА). Затем определяют продольные силы N0 и изгибающие моменты М0, как в арке постоянной жесткости, с соответствующей схемой опирания
Ввиду несовпадения плоскости действия расчетного момента для арки М0 и нормальной силы N0 с осью косяка, наклоненного к образующей свода под углом а, расчетный изгибающий момент для сквозного косяка
(8.1)
и нормальная сила для косяка
(8.2)
Расчет ведется с учетом совместного действия сжатия и изгиба. Гибкость свода с учетом пространственной работы его определяется по общей формуле с введением эмпирического коэффициента 0,7. Расчетная длина с учетом косого направления косяков увеличивается делением на sinα. Тогда
(8.3)
Для безметалльных сводов системы С. И. Песельника гибкость на основании ряда испытаний таких сводов рекомендуется принимать
(8.4)
где l0 — расчетная длина дуги свода, которая принимается при симметричной нагрузке для двухшарнирной арки l0 = 0,6S и для трехшарнирной арки l0 = 0,7S; при односторонней нагрузке в обоих случаях принимается l0 = 0,5S;
S — длина дуги свода.
Проверка напряжений в косяке производится по формуле:
(8.5)
или подставив значения Мк и Wк из формул (26.1) и (26.2), получим
где Fнт и Wнт — соответственно площадь и момент сопротивления нетто поперечного сечения косяка в середине его длины.
При малых значениях второго слагаемого, т. е. когда напряжение изгиба не превосходит 10% от напряжения сжатия косяка, ими следует пренебречь и ввести в знаменатель первого слагаемого коэффициент продольного изгиба φ, определяемый по расчетной гибкости λ.
Внецентренное примыкание к сквозному косяку двух набегающих косяков создает в нем изгибающий момент в другой плоскости, который предполагается погашенным настилом и при расчете обычно не учитывается.