1. Независимые случайные величины.

2. Аксиоматика Колмогорова.

3. Свойства математических ожиданий и дисперсий.

4. Основные неравенства теории вероятностей.

1. Неравенства теории вероятностей

При доказательстве многих теорем теории вероятностей и математической статистики используется ряд вспомогательных неравенств¹.

Неравенство Маркова. Если положительная случайная величина имеет конечное математическое ожидание , то для любого справедливо неравенство

. (4.1)

Неравенство Чебышёва. Если случайная величина имеет конечное математическое ожидание и дисперсию , то для любого справедливо неравенство

. (4.2)

Неравенство Йенсена. Для любой случайной величины и любой выпуклой [вогнутой] функции справедливо неравенство

[соответственно, ]. (4.3)

Неравенство Коши – Буняковского – Шварца. Для любых случайных величин , справедливо неравенство

. (4.4)

Неравенство Гёльдера. Для любых случайных величин , при 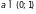справедливо неравенство

. (4.5)

Неравенство Минковского. Для любых случайных величин , при справедливо неравенство

. (4.6)

5. Центральная предельная теорема.

2. Центральная предельная теорема

Законы больших чисел устанавливают факт приближения среднего значения большого числа случайных величин к некоторым постоянным в виде сходимости последовательностей случайных величин по вероятности и почти наверное. Но этим не ограничиваются закономерности, возникающие в результате суммарного действия случайных величин. Центральная предельная теорема представляет собой группу теорем, утверждающих, что достаточно большая сумма сравнительно малых случайных величин распределена приближённо по нормальному закону.

Рассмотрим последовательность независимых случайных величин, и пусть , , .

Говорят, что для этой последовательности случайных величин выполняется условие Линдеберга, если

. (4.7)

Приведём строгую формулировку теоремы Ляпунова, одной из теорем, носящих название «центральная предельная теорема».

Если независимые случайные величины удовлетворяют условию Линдеберга (4.17), то случайная величина

сходится по распределению к стандартной нормальной случайной величине :

. (4.8)

В практических приложениях важно следующее следствие из теоремы Ляпунова:

Если независимые случайные величины имеют одинаковое распределение с , , то

, (4.9)

т. е.

. (4.10)

Пусть , тогда согласно следствию (4.20) из теоремы Ляпунова

, (4.11)

т. е. среднее арифметическое при сходится по распределению к нормальной случайной величине с параметрами .

В ряде задач приходится сталкиваться с ситуацией, когда исследуемая случайная величина является суммой большого числа независимых слагаемых, влияние каждого из которых на сумму очень мало. Такими случайными величинами являются, например, капиталы банков и страховых компаний (доля каждого отдельно взятого вкладчика не зависит от доли других вкладчиков и относительно мала, но в сумме все эти доли весьма весомы), выручка торговых предприятий (покупатели действуют независимо друг от друга и покупают товары на относительно небольшие суммы) и др.

На основании центральной предельной теоремы часто можно до наблюдения того или иного явления сказать, что соответствующая случайная величина должна иметь нормальное распределение или близкое к нему.

Приведём также два следствия из центральной предельной теоремы, относящиеся к независимым испытаниям. Локальная теорема Муавра – Лапласа утверждает:

Если вероятность успеха в каждом испытании отлична от нуля и единицы, а число испытаний достаточно велико, то для расчёта вероятности появления ровно успехов в серии из испытаний можно пользоваться приближённой формулой

( ), (4.12)

где — функция плотности нормального распределения (см. табл. П.1).

На практике, очевидно, вероятность появления любого конкретного числа успехов близка к нулю. Это имеет простое объяснение — ведь всего есть различных событий (может наступить успехов), и сумма вероятностей этих событий должна быть равна единице. Поэтому важно уметь вычислять вероятности того, что число успехов в серии из испытаний будет заключено между числами и . Для этого используется интегральная теорема Муавра – Лапласа:

Если вероятность успеха в каждом испытании отлична от нуля и единицы, а число испытаний достаточно велико, то для расчёта вероятности того, что число успехов в серии из испытаний будет заключено в промежутке , можно пользоваться приближённой формулой

( ), (4.13)

где — функция Лапласа (см. табл. П.1).

6. Закон больших чисел в общей форме.

12. Закон больших чисел. Предельные теоремы. Неравенство Чебышева. Теоремы Чебышева. Теорема Бернулли.

Изучение статистических закономерностей позволило установить, что при некоторых условиях суммарное поведение большого количества случайных величин почти утрачи-вает случайный характер и становится закономерным (иначе говоря, случайные отклоне-ния от некоторого среднего поведения взаимно погашаются). В частности, если влияние на сумму отдельных слагаемых является равномерно малым, закон распределения суммы приближается к нормальному. Математическая формулировка этого утверждения дается в группе теорем, называемой законом больших чисел.

Неравенство Чебышева.

Неравенство Чебышева, используемое для доказательства дальнейших теорем, справед-ливо как для непрерывных, так и для дискретных случайных величин. Докажем его для дискретных случайных величин.

неравенство Чебышева.

p( | X – M(X)| < ε ) ≥ D(X) / ε². (13.1)

Доказательство. Пусть Х задается рядом распределения

Х	х1	х2	…	хп
р	р1	р2	…	рп

Так как события |X – M(X)| < ε и |X – M(X)| ≥ ε противоположны, то р ( |X – M(X)| < ε ) + + р ( |X – M(X)| ≥ ε ) = 1, следовательно, р ( |X – M(X)| < ε ) = 1 - р ( |X – M(X)| ≥ ε ). Найдем р ( |X – M(X)| ≥ ε ).

D(X) = (x₁ – M(X))²p₁ + (x₂ – M(X))²p₂ + … + (x_n – M(X))²p_n . Исключим из этой суммы те слагаемые, для которых |X – M(X)| < ε. При этом сумма может только уменьшиться, так как все входящие в нее слагаемые неотрицательны. Для определенности будем считать, что отброшены первые k слагаемых. Тогда

D(X) ≥ (x_k+1 – M(X))²p_k+1 + (x_k+2 – M(X))²p_k+2 + … + (x_n – M(X))²p_n ≥ ε² (p_k+1 + p_k+2 + … + p_n).

Отметим, что p_k+1 + p_k+2 + … + p_n есть вероятность того, что |X – M(X)| ≥ ε, так как это сумма вероятностей всех возможных значений Х, для которых это неравенство справедливо. Следовательно, D(X) ≥ ε² р(|X – M(X)| ≥ ε), или р (|X – M(X)| ≥ ε) ≤ D(X) / ε². Тогда вероятность противоположного события p( | X – M(X)| < ε ) ≥ D(X) / ε², что и требо-валось доказать.