2. Балльное оценивание при принятии решения.
Для выбора лучшего варианта решения применяют и балльное оценивание. Возможны два подхода. При первом из них каждому члену группы даются 10 или 20 баллов, которые ему предлагается распределить между рассматриваемыми вариантами в соответствии с его системой предпочтений. После чего вариант, получивший от всех членов группы наибольшую сумму баллов, и выбирается группой как наилучший. Указанный подход иллюстрируется таблицей 2.4.
Таблица 2.4. Балльное оценивание. Подход 1
Варианты |
эксп.1 |
эксп.2 |
эксп.3 |
эксп.4 |
эксп.5 |
сумма баллов |
коллект. ранжировка |
A |
3 |
1 |
1 |
0 |
3 |
8 |
4–5 |
B |
3 |
3 |
3 |
4 |
2 |
15 |
3 |
C |
3 |
2 |
2 |
1 |
0 |
8 |
4–5 |
D |
3 |
5 |
4 |
7 |
7 |
26 |
2 |
E |
8 |
5 |
10 |
5 |
7 |
35 |
1 |
F |
0 |
2 |
0 |
2 |
1 |
5 |
6 |
G |
0 |
2 |
0 |
1 |
0 |
3 |
7 |
Как видно из представленного в таблице 2.4 примера, эксперты вольны приписывать каждому варианту любое количество баллов из имеющихся в их распоряжении 20. А некоторые варианты могут вообще не получить ни одного балла. В данной задаче вариант E набрал наибольшую сумму баллов (35) и выбирается как наилучший. Рассмотренная методика может применяться и в два этапа. На первом из них из всего количества вариантов для дальнейшего анализа отбирается несколько наиболее предпочтительных. Для этого заранее оговаривается, что ко второму этапу будут допущены только варианты, набравшие не менее определенной суммы баллов. Например, если в рассматриваемом примере эта контрольная сумма устанавливается в 15 баллов, то ко второму этапу будут допущены варианты E, D и B. На втором этапе вся процедура балльного оценивания повторяется, но теперь только для выделенных трех вариантов, в результате чего и находится лучший из них.
Применять указанную методику для нахождения лучшего варианта нецелесообразно, поскольку при ее использовании мнения экспертов далеко не всегда оказываются согласованными. Эксперты зачастую отдают все 20 баллов предпочитаемому ими варианту и, таким образом, сравнения вариантов практически не происходит. Рекомендуемая область применения этой методики – отбраковка наименее предпочтительных вариантов и формирование множества вариантов, из которых и будет впоследствии находиться наилучший.
При втором подходе каждый вариант оценивается, например, по 10 балльной шкале, а затем по наибольшей сумме баллов определяется лучший из них. Процедура иллюстрируется примером, помещенным в таблице 2.5.
Таблица 2.5. Балльное оценивание. Подход 2
Варианты |
эксп.1 |
эксп.2 |
эксп.3 |
эксп.4 |
эксп.5 |
сумма баллов |
колл. ранжировка |
A |
5 |
6 |
5 |
3 |
2 |
21 |
5 |
B |
8 |
8 |
9 |
9 |
8 |
42 |
2 |
C |
1 |
2 |
2 |
2 |
1 |
8 |
7 |
D |
4 |
4 |
5 |
5 |
4 |
22 |
4 |
E |
10 |
9 |
8 |
9 |
8 |
44 |
1 |
F |
3 |
4 |
3 |
2 |
3 |
15 |
6 |
G |
6 |
7 |
7 |
7 |
6 |
33 |
3 |
Из приведенного примера видно, что эксперты лучшим вариантом признали вариант E, набравший наибольшую сумму баллов (44).
Проблема проверки согласованности мнений экспертов существует и при балльном оценивании. Решается она следующим образом. Вначале для каждого варианта решения (их в рассматриваемом примере 7) определяется среднее арифметическое из оценок всех экспертов. Так, для варианта E (см. таблицу 2.5), оно равно Xср = (10+9+8+9+8):5 = 44:5 = 8,8. Затем рассчитывается среднее квадратическое отклонение по формуле
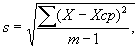
где X – оценки экспертов, m – число экспертов.
Для нашего примера имеем:
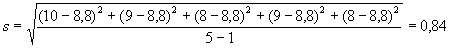
Далее подсчитывается коэффициент вариации по формуле
K = s/Xср = 0,84/8,8 = 0,095.
Мнения экспертов по каждому из вариантов решения считаются согласованными, если коэффициент вариации не превосходит величины 0,25. Для варианта решения E в рассматриваемом примере получаем s = 0,095<0,25. Таким образом мнения экспертов, представленные их оценками по варианту решения E, считаются согласованными. И подобная проверка, в принципе, должна проводиться для каждого варианта. Напомним, что в нашем примере их 7. Однако часто в этом не возникает необходимости, если согласованы мнения относительно наиболее предпочтительных вариантов.
Возникает резонный вопрос, что же делать, если мнения окажутся несогласованными. Возможностей здесь несколько. Во-первых, информацию о несогласованности мнений экспертов можно просто принять к сведению и этим ограничиться. Во-вторых, согласно [18], рекомендуется заново провести всю процедуру экспертного оценивания, предварительно ознакомив экспертов с результатами экспертизы. Если и после вторичной экспертизы мнения экспертов останутся несогласованными, то следуя ГОСТу, из оценок экспертов исключают оценку, наиболее отличающуюся от среднего арифметического значения и заново проводят проверку согласованности. И так до тех пор, пока оценки оставшихся экспертов не окажутся согласованными. Более подробно это изложено в [18].
При принятии решений с помощью экспертного оценивания одним из важных вопросов остается вопрос определения компетентности экспертов. Об этом и о других проблемах, связанных с экспертным оцениванием, читатель может получить достаточную информацию, обратившись к [18]. Проблемы эти, безусловно, существуют. Иначе не получил бы такого широкого распространения анекдот о Шерлоке Холмсе и докторе Ватсоне, когда они на воздушном шаре приземлились в тумане на незнакомой местности. У подошедшего человека Холмс спрашивает: "Скажите, пожалуйста, где мы находимся?" Получив ответ: "Вы находитесь в гондоле воздушного шара", – Холмс заключает: "Этот человек работает экспертом". – "Почему Вы так решили?" – спрашивает Ватсон. – "Он дал абсолютно точный ответ и абсолютно бесполезный".
a