4.3.2. Практический расчет закрытой цилиндрической зубчатой передачи (редуктора)

Расчет проводится после определения силовых и кинематических параметров привода, в котором применена передача.

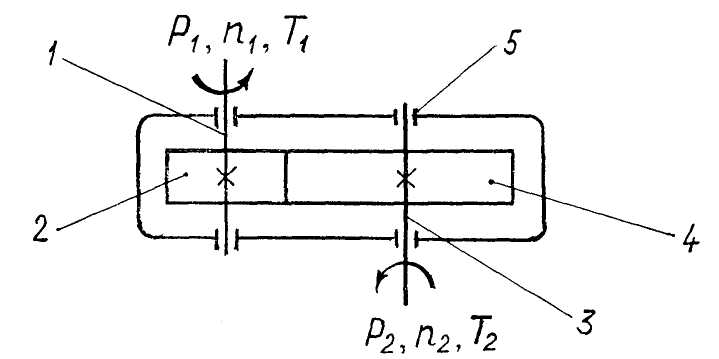
Рис. 4.8. Схема к расчету зубчатой передачи

В результате становятся известными:

Р₁– мощность на ведущем валу передачи, кВт;

n₁– частота вращения ведущего вала, об/мин;

u – передаточное число редуктора.

Затем определяется силовой (вращающий момент) и кинематический (частота вращения) параметры самой передачи. Частота вращения выходного вала (об/мин) определится:

.

Вращающий момент на быстроходном валу ( ):

.

Вращающий момент на тихоходном валу определится ( ):

,

где η_з – кпд зубчатого зацепления, для закрытой передачи η_з=0,96…0,97, для открытой – η_з=0,93…0,95.

η_п – кпд подшипниковых опор, для одной пары подшипников качения – η_п=0,98…0,99.

к – показатель степени, равный числу пар подшипников.

Проектный расчет передачи

а. Выбор материала зубчатых колес

Основным материалом для изготовления зубчатых колес в настоящее время является сталь. В условиях мелкосерийного и индивидуального производства применяются стали с твердостью 350 НВ. При этом чистовое нарезание зубьев производится после термообработки, обеспечивается точность изготовления и хорошая прирабатываемость зубьев.

Для равномерного изнашивания зубьев и лучшей их прирабатываемости твердость шестерни назначается большей, чем твердость колеса:

НВ₁ - НВ₂ = 20…50,

где НВ₁ – твердость материала шестерни;

НВ₂ – твердость материала колеса.

Обычно для шестерни и колеса назначают сталь одной марки с различными видами термообработки. Характеристики сталей приведены в табл. 4.4.

б. Определение допускаемых контактных напряжений

Эти напряжения определяются отдельно для зубьев шестерни [σ]_Н1 и зубьев колеса [σ]_Н2 в следующем порядке.

1. Определяем коэффициент долговечности К_HL:

,

где N_HO – число циклов перемены напряжений, соответствующий пределу выносливости (согласно табл. 4.5);

N – число циклов перемены напряжений за срок службы (наработка):

, где

n – частота вращения вала шестерни или колеса, об/мин. Если N>N_HO, то принимается K_HL=1.

Т а б л и ц а 4.4

Механические характеристики сталей

Марка стали	Термо-обработка	Твердость, НВ	Предел прочности, σВ, МПа	Предел текучести σТ, МПа
35	Н	163…192	550	270
40	У	192…228	700	400
45	Н	179…207	600	320
45	У	235…262	780	540
40Х	У	235…262	790	640
40ХН	У	269…302	920	750
35ХМ	У	269…302	920	790

Примечания:

1. В обозначении сталей первые цифры – содержание углерода в сотых долях процента; буквы – лигирующие элементы: Х – хром, Н – никель, М – молибден (содержание до 1%).

2. Обозначение термообработки: У – улучшение, Н – нормализация.

Таблица 4.5

Значение числа циклов

Средняя твердость поверхности зубьев, НВср	200	250	300	350	400
NHO, млн циклов	10	16,5	25	36,4	50

2. Определяем допускаемые контактные напряжения, соответствующие пределу контактной выносливости при числе циклов N_HO, МПа :

для шестерни [σ]_НО1=2НВ₁+70;

для колеса [σ]_НО2=2НВ₂+70.

3. Определяем допускаемые контактные напряжения для зубьев шестерни и колеса:

;

.

В дальнейшем расчет ведется по наименьшему из найденных значений, т.е. по менее прочным зубьям (шестерни или колеса).

в. Определение допускаемых напряжений изгиба

Эти напряжения определяются отдельно для зубьев шестерни [σ]_F1 и колеса [σ]_F2 в следующем порядке.

1. Определяем коэффициент долговечности К_FL:

,

где N_FO – число циклов перемены напряжений, соответствующее пределу выносливости, для всех марок сталей;

N – число циклов перемены напряжений за срок службы, (см. п.б, 1).

Если N>N_FO, то принимается K_FL=1.

2. Определяем допускаемые напряжения изгиба, соответствующие пределу изгибной выносливости при числе циклов N_FO, МПа:

для шестерни [σ]_FО1=1,8 НВ₁;

для колеса [σ]_FО2=1,8 НВ₂.

3. Определяем допускаемые напряжения изгиба для зубьев шестерни и колеса (МПа):

,

.

Для реверсивных передач полученные значения уменьшить на 25%. Найденные значения напряжений изгиба используются при проверочном расчете.

г. Определение геометрических параметров передачи

Расчеты ведем в следующем порядке:

1. Определяем главный параметр – межосевое расстояние:

,

где К_а – вспомогательный коэффициент, К_а=430 – для косозубых передач,

К_а=495 – для прямозубых передач;

– коэффициент ширины венца колеса;

b₂ – ширина венца колеса (рис. 4.9);

ψ_а=0,28…0,36 – для симметрично расположенного относительно опор колеса;

ψ_а=0,2…0,25 – для консольно расположенного колеса;

К_Нβ – коэффициент неравномерности нагрузки по длине зуба, для прирабатывающихся зубьев К_Нβ=1;

[σ]_Н – допускаемое контактное напряжение колеса с менее прочным зубом (см. п. б, 3).

Т а б л и ц а 4.6

Нормальные линейные размеры в интервале 63-975 мм, по ГОСТ 6636-69*

Ряды				Дополни-тельные размеры	Ряды				Дополни-тельные размеры
Ra5	Ra10	Ra20	Ra40		Ra5	Ra10	Ra20	Ra40
63	63	63	63 67	65 70 73 78 82 88 92 98 102 108 112 115 118 135 145 155 165 175 185 195 205 215 230	250	250	250	250 260	270 290 310 330 350 370 390 410 440 460 490 515 545 580 615 650 690 730 775 825 875 925 975
		71	71 75				280	280 300
	80	80	80 85			320	320	320 340
		90	90 95				360	360 380
100	100	100	100 105		400	400	400	400 420
		110	110 120				450	450 480
	125	125	125 130			500	500	500 530
		140	140 150				560	560 600
160	160	160	160 170		630	630	630	630 670
		180	180 190				710	710 750
	200	200	200 210			800	800	800 850
		220	220 240				900	900 950

Полученную величину необходимо округлить до ближайшего значения из ряда R_a40 нормальных линейных размеров. Допускается использовать дополнительный ряд чисел (табл.4.6).

2. Определяем модуль зацепления:

– для прирабатывающихся зубьев при твердости 350 НВ.

Полученное значение модуля округлить до ближайшего большего из стандартного ряда (табл. 4.7). При выборе модуля первый ряд следует предпочитать второму. В силовых передачах принять .

3. Определяем ширину венца колеса:

.

Полученное значение округлить до целого числа.

Примечания:

1. При выборе размеров предпочтение должно отдаваться рядам с более крупной градацией.

2. Дополнительные размеры допускается применять в технически обоснованных случаях.

Т а б л и ц а 4.7

Значения стандартных модулей

Ряды	Модуль, m, мм
1-й	1; 1,25; 1,5; 2; 2,5; 3; 4; 5; 6; 8; 10; 12; 16; 20; 25
2-й	1,125; 1,375; 1,75; 2,25; 2,75; 3,5; 4,5; 5,5; 5,7; 7; 9; 11; 14

3. Определяем ширину венца шестерни (мм):

.

4. Определяем угол наклона зубьев β_min для косозубых передач:

.

Этот угол составляет 8…16⁰. Для уменьшения осевых сил F_a в зацеплении, желательно получить его меньшие значения (изменением m и b₂).

5. Определяем суммарное число зубьев шестерни и колеса:

для прямозубых колес ;

для косозубых колес .

Полученные значения округлить в меньшую сторону до целого числа.

6. Уточняем угол наклона зубьев:

.

7. Определяем число зубьев шестерни:

.

Значение округлить до ближайшего числа. Из условия отсутствия подрезания зубьев и уменьшения шума рекомендуется принимать .

8. Определяем число зубьев колеса: .

9. Определяем фактическое передаточное число: .

10. Определяем отклонение передаточного числа от заданного (погрешность): .

При невыполнении этого условия пересчитать Z₁ и Z₂.

11. Определяем фактическое межосевое расстояние:

для прямозубых передач ;

для косозубых передач .

12. Определяем основные геометрические размеры зубчатых колес, (рис. 4.9) и результаты расчета сводим в табл. 4.8.

Т а б л и ц а 4.8

Геометрические размеры колес

Диаметр	Шестерня		Колесо
	Прямозубая	Косозубая	Прямозубое	Косозубое
Делительный, d
Вершин зубьев, da
Впадин зубьев, df

Примечание: Точность вычислений d – до 0,1 мм.

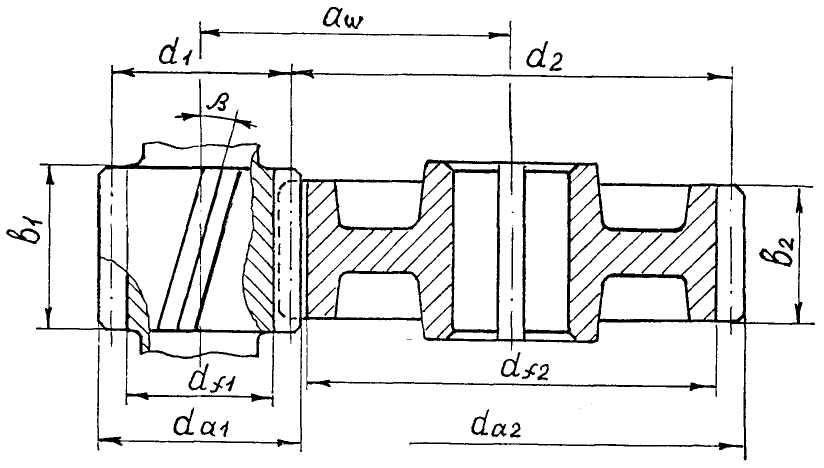
Рис. 4.9. Геометрические параметры цилиндрической зубчатой передачи: a_w – межосевое расстояние; d₁, d₂ – диаметры делительных окружностей; d_a1, d_a2 – диаметры вершин зубьев; d_f1, d_f2 – диаметры впадин зубьев; b₁, b₂ – ширина венца зубьев; β – угол наклона зубьев

Проверочный расчет передачи

а) проверяем межосевое расстояние (мм): .

б) определяем окружную силу в зацеплении (Н): .

в) определяем окружную скорость колеса (м/с) и назначаем степень точности передачи (табл.4.9): .

г) проверяем контактные напряжения:

,

где К – вспомогательный коэффициент, К=436 – для прямозубых передач;

К=376 – для косозубых передач;

К_Нα – коэффициент распределения нагрузки между зубьями,

К_Нα=1 – для прямозубых колес, для косозубых К_Нα определяется по номограмме (рис. 4.10);

К_НV – коэффициент динамической нагрузки, зависящий от окружной скорости колес и степени точности передачи (табл. 4.10);

К_Нβ=1, см. проектный расчёт, п. г,1.

Т а б л и ц а 4.9

Степени точности зубчатых передач

Степень точности	Окружные скорости колес, V, м/с
	Прямозубые	Косозубые
6	до 15	до 30
7	до 10	до 15
8	до 6	до 10
9	до 2	до 4

Допускаемая недогрузка передачи (σ_Н<[σ]_H) не более 10%, а перегрузка не более 5%. Если условие прочности не выполняется, то следует изменить ширину венца колеса b₂, или увеличить межосевое расстояние a_w, или назначить другие материалы колес и термообработку и расчет повторить.

д) Проверяем изгибные напряжения зубьев шестерни и колеса:

,

где [σ]_F1, [σ]_F2 – допускаемые напряжения изгиба для зубьев шестерни и колеса (см. проектный расчёт п. в,3);

К_Fα – коэффициент распределения нагрузки между зубьями;

K_Fα=1 – для прямозубых колес; для косозубых – K_Fα определяется по табл. 4.11, в зависимости от степени точности передачи;

K_Fβ – коэффициент неравномерности нагрузки по длине зуба, для прирабатывающихся зубьев K_Fβ=1.

К_FV – коэффициент динамической нагрузки, зависит от окружной скорости и степени точности передачи (см. табл. 4.10);

Т а б л и ц а 4.10

Значения коэффициентов K_HV и K_FV при НВ₂ 350

Степень точности	Коэффи-циент	Окружная скорость, V, м/с
		1	2	4	6	8	10
6	КHV KFV	1,03 1,01 1,06 1,02	1,06 1,02 1,13 1,05	1,12 1,03 1,26 1,10	1,17 1,04 1,40 1,15	1,23 1,06 1,58 1,20	1,28 1,07 1,67 1,25
7	КHV KFV	1,04 1,02 1,08 1,03	1,07 1,03 1,16 1,06	1,14 1,05 1,33 1,11	1,21 1,06 1,50 1,16	1,29 1,07 1,67 1,22	1,36 1,08 1,80 1,27
8	КHV KFV	1,04 1,01 1,10 1,03	1,08 1,02 1,20 1,06	1,16 1,04 1,38 1,11	1,24 1,06 1,58 1,17	1,32 1,07 1,78 1,23	1,40 1,08 1,96 1,29
9	КHV KFV	1,05 1,01 1,13 1,04	1,10 1,03 1,28 1,07	1,20 1,05 1,50 1,14	1,30 1,07 1,77 1,21	1,40 1,09 1,98 1,28	1,50 1,12 2,25 1,35

Примечание: В числителе данные для прямозубых колес, в знаменателе – для косозубых колес.

Y_F1, Y_F2 – коэффициенты формы зуба шестерни и колеса. Для прямозубых передач определяется в зависимости от числа зубьев Z₁, Z₂; для косозубых – в зависимости от эквивалентного числа зубьев шестерни и колеса по табл. 4.12:

; .

Y_β – коэффициент, учитывающий наклон зубьев. Y_β=1 – для прямозубых колес, – для косозубых колес.

Если при проверочном расчете σ_F<<[σ]_F, то это допустимо, так как нагрузочная способность большинства передач ограничивается контактной прочностью.

Если σ_F>[σ]_F свыше чем на 5 %, то необходимо увеличить модуль m, пересчитать число зубьев Z₁ и Z₂ и повторить проверочный расчет на изгиб. Так как межосевое расстояние остается без изменения, то и контактная прочность не изменится.

Т а б л и ц а 4.11

Значения коэффициента К_Fα

Степень точности	6	7	8	9
Коэффициент КFα	0,72	0,81	0,91	1,00

Т а б л и ц а 4.12

Коэффициенты формы зуба Y_F1, Y_F2

Z или ZV	YF	Z или ZV	YF	Z или ZV	YF	Z или ZV	YF
16	4,28	25	3,90	35	3,75	65	3,62
17	4,27	26	3,88	40	3,70	71	3,61
20	4,07	28	3,81	45	3,66	80	3,61
22	3,98	30	3,80	50	3,65	90	3,60
24	3,92	32	3,78	60	3,62	100	3,60

Рис. 4.10. График определения коэффициента К_Нα