4.3. Передачи зацеплением

4.3.1. Зубчатые передачи

Служат для преобразования параметров вращательного движения или вращательного движения в поступатель­ное. Принцип действия основан на зацеплении пары зубчатых колес или зубчатого колеса и зубчатой рейки.

Меньшее из зубчатых колес пары называют шестерней, большее – колесом, а термин «зубчатое колесо» является общим. Сектор зубчатого колеса бесконечно большого диаметра называют рейкой.

Наиболее распространены зубчатые цилиндрические передачи с внешним или с внутренним зацеплением, оси валов которых параллельны, а также зубчатые конические – оси валов которых пересекаются или перекрещиваются (рис. 4.5).

Зубчатые колеса бывают с прямыми, косыми или шевронными («в елочку») зубьями. Косозубые колеса обеспечивают более плавный ход передачи, но при их работе возникают осевые усилия, которые должны воспринимать опоры валов. У колес с шевронными зубьями осевые усилия взаимно уравновешиваются, но изготовление таких колес более сложное.

Профиль зубьев обычно эвольвентный (т.е. их боковые поверхности очерчены отрезками эвольвенты – левой и правой). Этот профиль позволяет зубьям при вращении колес обкатываться друг по другу, что обеспечивает плавность работы и небольшие потери энергии на трение в зацепле­нии.

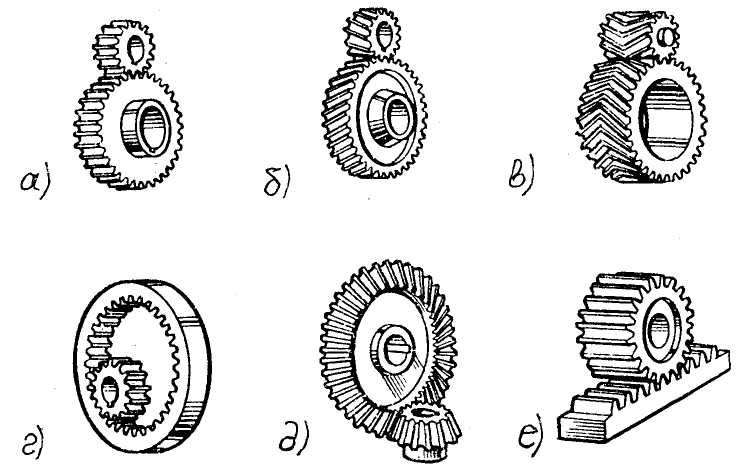
Рис. 4.5. Зубчатые передачи: а) - прямозубая; б) - косозубая; в) - шевронная; г) - цилиндрическая с внутренним зацеплением; д) - коническая; е) - зубчато-реечная

Зацепление зубчатых колес (рис.4.6) эквивалентно качению без скольжения окружностей, с диаметрами d_ω1 и d_ω2. Эти окружности назы­вают начальными. Передаточное число выразится (см. раздел 4.2.1):

. (4.12)

Однако диаметры d_ω1 и d_ω2 в реальной передаче трудно замерить, поэтому передаточное число выражают через другие, более удобные для измерений величины.

Зацепление зубчатых колес в передаче требует основного условия: зуб одного колеса должен точно входить в соответствующую ему при зацеплении впадину другого колеса. Ширину зуба и впадины рассчитывают на диаметрах делительных окружностей. Для стандартных зубчатых колес делительная окружность совпадает с начальной: , .

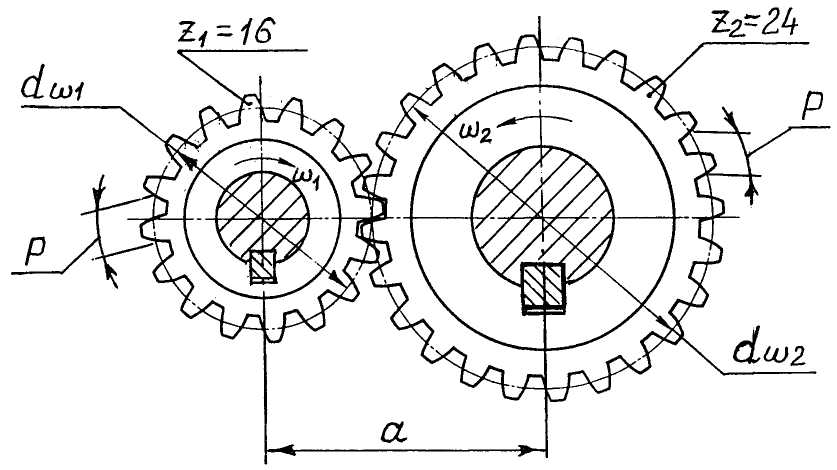
Рис. 4.6. Зубчатая цилиндрическая передача и ее элементы: z₁ z₂ - количество зубьев шестерни и колеса; Р - окружной шаг; d_ω1, d_ω2- диаметры начальных окружностей; а - межосевое расстояние

Расстояние между одноименными профилями соседних зубьев, измеренное по дуге делительной окружности, называют окружным делительным шагом и обозначают Р.

Таким образом, зубчатое зацепление возможно лишь при равенстве окружных шагов шестерни и колеса. Окружный шаг определится: для шестерни - , для колеса , где z₁ и z₂ – количество зубьев шестерни и колеса. Откуда следует: или, после преобразования, имеем . Так как , то можно сделать вывод: , т.е. передаточное число зубчатой передачи выражается через отношение количества зубьев ведомого и ведущего колес.

Основным геометрическим параметром зубчатого колеса является модуль – линейная величина в π раз меньшая окружного шага: m=P/. Для пары колес, находящихся в зацеплении, модуль должен быть одинаковым. Численные значения модулей для цилиндрических и конических колес стандартизированы.

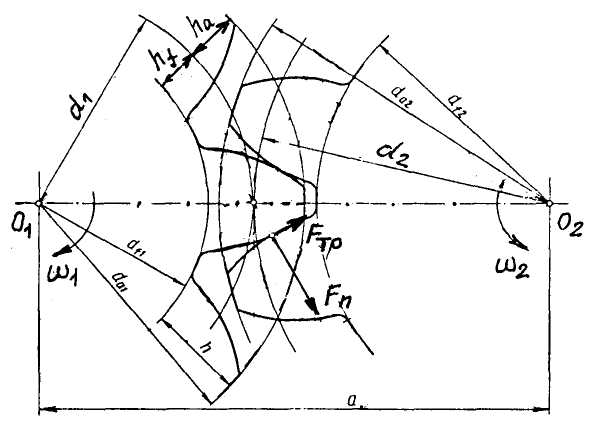
Рис. 4.7. Элементы зубчатого зацепления

Все основные параметры зубчатых колес выражают через модуль. Для цилиндрического зубчатого колеса эти параметры запишутся:

• шаг зубьев p = πm;

• высота головки зуба h_a = m;

• высота ножки зуба h_f = 1,25m;

• диаметр делительной окружности d = mz;

• диаметр окружности вершин ;

• диаметр окружности впадин ;

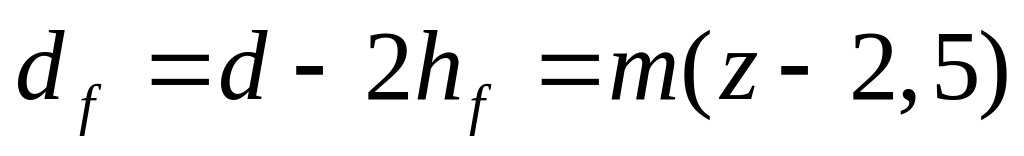• межосевое расстояние .

Критерием работоспособности зубчатых передач являются износостойкость активных поверхностей зубьев и их прочность на изгиб. При передаче вращающего момента в зацеплении действует нормальная сила F_n и сила трения , возникающая в результате относительного скольжения зубьев. Под действием этих сил зуб находится в сложном напряженном состоянии, в нем возникают напряжения изгиба σ_F и контактные напряжения σ_Н. Эти напряжения действуют на зуб только во время нахождения его в зацеплении, т.е. являются повторно-переменными. Эти напряжения вызывают появление усталостных трещин у основания зуба, отслаивание и выкрашивание материала на активной поверхности ножек зуба.

При проектном расчете передачи определяются ее геометрические параметры по допускаемым контактным напряжениям. При проверочном – проверяются зубья по контактным и изгибным напряжениям.

Достоинства зубчатых передач – высокий кпд (0,97…0,99 в одной ступени), компактность, по сравнению с другими видами передач, постоянство передаточного числа из-за отсутствия проскальзывания, долговечность и надежность. Недостатки – сложность изготовления и повышенные требования к точности, шум при больших скоростях.