Модель «следовать за лидером» Штаккельберга

Модель Штаккельберга возникает из модели Курно, когда спрашивают, что слу­чится, если ожидания одной фирмы по поводу реакции другой окажутся верны? Таким образом, мы возвращаемся к модели Курно и рассматриваем две фирмы, которые обслуживают спрос с линейной динамикой и производят недифференцированный продукт с одинаковыми и постоянными предельными издержками и для которых стра­тегической переменной является объем производства.

Каждая фирма придерживает­ся предположительных изменений Курно, т.е. каждая считает, что уровень производ­ства другой фирмы не будет изменяться в зависимости от ее собственных решений. Рис. 5.3 представляет функцию реакции по Курно для каждой фирмы. Определяя уро­вень производства фирмы 2 на вертикальной оси, мы движемся по горизонтали к R₁ и затем по вертикали вниз до горизонтальной оси, чтобы определить максимизирующий прибыль ответ фирмы 1 по Курно.

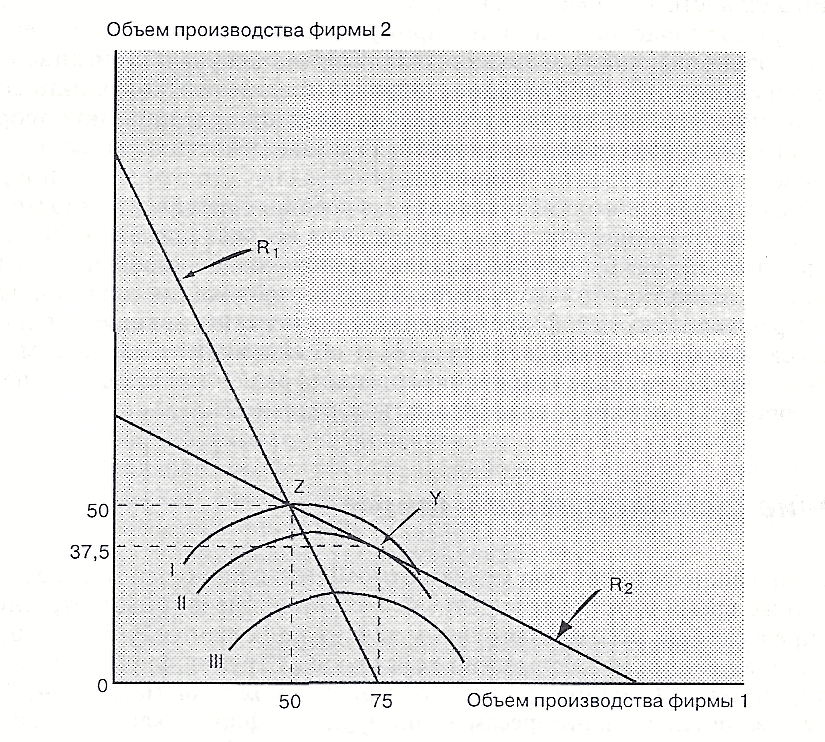
Рис. 5.3 Равновесие Штаккельберга для двух фирм.

Важно отметить следующее:

1. Так как в данном примере предполагается линейный спрос и постоянные для каждой фирмы предельные издержки, функция реакции будет прямой линией.

2. Так как конкуренция происходит по поводу объема производства, а не по поводу цен кривые изоприбыли выпуклы верх и изгибаются по направлению к осям координат, а не от них.

3. Чем ближе кривая к оси тем, выше уровень прибыли. При постоянном уровне собственно­го производства прибыль растет в случае сокращения производства конкурентом (на­пример, кривая изоприбыли III представляет более высокий уровень прибыли, чем кривые I и II).

4. Кривые реакции количества наклонены вниз. Оптимальной реакцией фирмы 1 на снижение объема выпуска фирмой 2 является увеличение производства.

Математическая модель Штаккельберга (дуополия)

Представленный в тексте главы анализ модели Штаккельберга начинается с численного примера модели дуополии Курно. Линейная функция спроса имеет при а = 200, b = 1 вид:

.

У каждой фирмы постоянные предельные издержки равны с = 50. Таким образом, прибыль фирмы 1 равна:

.

Демонстрируя поведение по Курно, каждая фирма предполагает, что другая будет поддерживать производство на постоянном уровне. При этой предпосылке функция реакции фирмы 1 может быть найдена подстановкой принятых значений a, b и с в уравнение определения объема производства:

.

Фирма 2 решает идентичную проблему с тем, чтобы получить такую функцию реакции R₂:

.

Равновесное решение лежит на пересечении двух кривых реакции:

.

Поскольку фирмы 1 и 2 идентичны, можно подставить этот результат в формулу определения цены:

В модели Штаккельберга одна фирма (фирма 2) «следует» за другой, максимизируя прибыль на основе предпосылки, что выпуск другой фирмы, фиксирован, т.е. она продолжает сохранять предположительное изменение по Курно. Однако «лидер» (здесь лидер фирма 1) признает это поведение «последователя» и включает функцию реакции «последователя» в свое решение задачи максимизации прибыли. В этом случае функция реакции будет прямой линией. Таким образом, наклон R₂ равен предположительному изменению фирмы 1:

.

Чтобы определить максимизирующий прибыль объем производства фирмы 1, преобразуем условие первого порядка в функцию q₁ подстановкой -0,5 вместо dq₂/dq₁ и в функцию реакции фирмы 2 для q₂:

,

при котором q₁ = 75. Подставляя это значение обратно в функцию реакции фирмы 2 с тем, чтобы получить q₂ = 75 – 0,5(75) = 37,5. Графически это решение возникает тогда, когда движение фирмы 1 на более высокую кривую изоприбыли совместно с реакциями фирмы 2, т.е. в точке касания изоприбыли II и R₂ на рис. 5.3.

Логика модели Штаккельберга

Когда обе фирмы придерживаются предположительных изменений по Курно, рав­новесие будет в точке Z — на пересечении двух кривых реакции. Допустим, что в этой точке обе фирмы производят по 50 единиц продукции. Предположим, одна­ко, что фирма 1 признает, что фирма 2 отвечает в соответствии с ее кривой реакции R₂.

Существует область, где фирма 1 может увеличить объем производства, передвигаясь от Z к R₂ (в ожидании ответа фирмы 2), и тем самым оказаться на более высокой кривой изоприбыли (ближе к горизонтальной оси). Предел этой последовательности определя­ется точкой касания кривой изоприбыли (в данном случае II) и кривой реакции R₂, где q₁ = 75. Если бы фирма 1 увеличила производство за пределы данного уровня, ответ фирмы 2, по Курно, переместил бы фирму 1 на более низкую кривую изоприбыли (более удаленную от горизонтальной оси).

Точка касания Y (где фирма 1 производит 75 и фирма 2 - 37,5 единицы продукции) является точкой равновесия по Штаккельбергу. Фирма 1 называется «лидером» по Штаккельбергу, поскольку она принимает на себя инициативу в определении объема производства, в то время как фирма 2 называ­ется «последователем» — она принимает производство «лидера» как данный факт.