7. Карти Карно і діаграми Вейча.

Якщо число логічних змінних не перевищує 5-6, перетворення логічних рівнянь зручно робити за допомогою карт Карно або діаграм Вейча. Ціль перетворень - одержання компактного логічного виразу (мінімізація). Мінімізацію роблять об'єднанням наборів (термів) на карті Карно. Поєднувані набори повинні мати однакові значення функції (усі 0 або всі 1).

Для наочності розглянемо приклад: нехай потрібно знайти логічні вирази для мажоритарної функції fm трьох змінних X, Y, Z, що описуються наступною таблицею істинності:

Таблиця 7.2

N	X	Y	Z	fm
0	0	0	0	0
1	0	0	1	0
2	0	1	0	0
3	0	1	1	1
4	1	0	0	0
5	1	0	1	1
6	1	1	0	1
7	1	1	1	1

Складемо карту Карно. Вона являє собою щось схоже на таблицю, у якій найменування стовпців і рядків являють собою значення змінних, причому змінні розташовуються в такому порядку, щоб при переході до сусіднього стовпця або рядка змінювалося значення тільки однієї змінної. Наприклад, у рядку XY таблиці 7.3 значення змінних XY можуть бути представлені наступними послідовностями: 00, 01, 11, 10 і 00, 10, 11, 01. Таблицю заповнюють значеннями функції, що відповідають комбінаціям значень змінних. Отримана в такий спосіб таблиця виглядає, як показано нижче (таблиця 7.3).

Таблиця 7.3

XY Z	00	01	11	10
0	0	0	1	0
1	0	1	1	1

Н а карті Карно відзначаємо групи, що складаються з 2ⁿ осередків (2, 4, 8,...) і утримуючі 1, тому що вони описуються простими логічними виразами. Три прямокутники в таблиці визначають логічні вирази XY, XZ, YZ. Кожен прямокутник, що поєднує два осередки, відповідає логічним перетворенням:

,

,

.

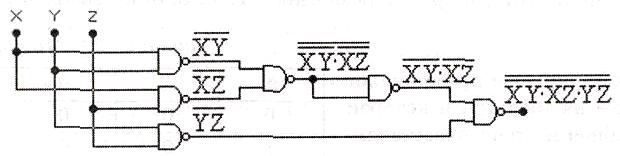
Компактний вираз, що описує функцію, являє собою диз'юнкцію отриманих за допомогою карт Карно логічних виразів. У результаті одержуємо вирази в диз'юнктивній формі: fm = XY v XZ vYZ.

Для реалізації функції мажоритарної логіки трьох логічних змінних необхідно реалізувати схему, що при подачі на її входи трьох сигналів формувала б на виході сигнал, рівний сигналу на більшості входів ( 2 з 3 або 3 з 3). Ця схема корисна для відновлення дійсного значення сигналів, що надходять на 3 входи, якщо можлива відмова на одному з входів.

Для реалізації функції на елементах 2І-НІ перетворимо отримані вирази в базис елементів І-НІ, тобто, запишемо вирази за допомогою операцій логічного множення й інверсії. Перевірити справедливість кожного з приведених виразів для fm можна прямою підстановкою значень X, Y, Z з таблиці 7.2:

Відповідна схемна реалізація приведена на мал. 7.1.

Мал. 7.1