2. Гидростатика. Силы, действующие в жидкости. Гидростатическое давление и его свойства.

Гидростатикой называется раздел гидравлики, в котором рассматриваются законы равновесия жидкости и их практическое применение.

Жидкости делятся на покоящиеся и движущиеся.

Здесь же рассмотрим силы, которые действуют на жидкость и вне ее в общем случае.

Сами эти силы можно разделить на две группы.

1. Силы массовые. По-другому эти силы называют силами, распределенными по массе: на каждую частицу с массой ΔM = ρW действует сила ΔF, в зависимости от ее массы.

Пусть объем ΔW содержит в себе точку А. Тогда в точке А:

где FА – плотность силы в элементарном объеме.

Плотность массовой силы – векторная величина, отнесена к единичному объему ΔW; ее можно проецировать по осям координат и получить: Fx, Fy, Fz. То есть плотность массовой силы ведет себя, как массовая сила.

Примерами этих сил можно назвать силы тяжести, инерции (кориолисова и переносная силы инерции), электромагнитные силы.

Однако в гидравлике, кроме особых случаев, электромагнитные силы не рассматривают.

2. Поверхностные силы. Таковыми называют силы, которые действуют на элементарную поверхность Δw, которая может находиться как на поверхности, так и внутри жидкости; на поверхности, произвольно проведенной внутри жидкости.

Таковыми считают силы: силы давления которые составляют нормаль к поверхности; силы трения которые являются касательными к поверхности.

Если по аналогии (1) определить плотность этих сил, то:

нормальное напряжение в точке А:

касательное напряжение в точке А:

И массовые, и поверхностные силы могут быть внешними, которые действуют извне и приложены к какой-то частице или каждому элементу жидкости; внутренними, которые являются парными и их сумма равна нулю.

Наличие касательной силы Т привело бы к появлению касательного напряжения жидкости, которые возникают только при ее движении.

Поэтому в покоящейся жидкости наблюдается только нормальная сила N. Она получила название – сила гидростатического давления.

Р – нормальная сжимающая сила.

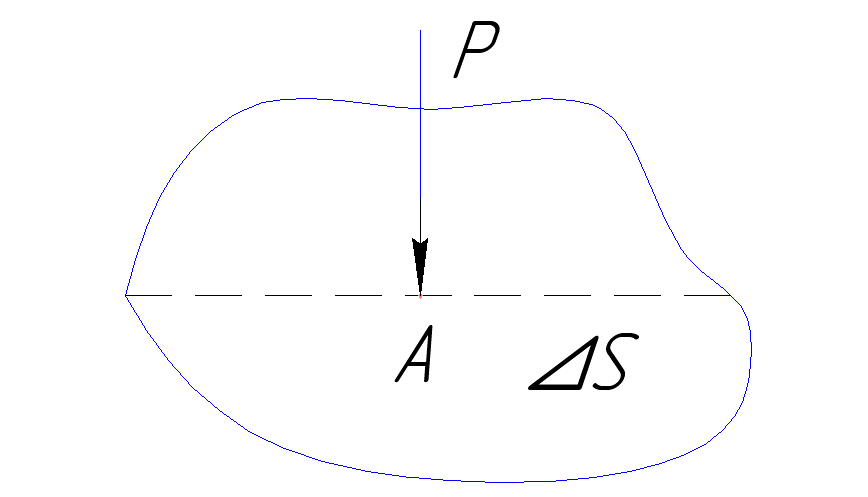
[Н/м²] Свойства гидростатического давления получили название закон Паскаля.

Свойства гидростатического давления:

1. Направлено внутрь объёма жидкости перпендикулярно поверхности твердого тела, ограничивающего жидкость.

2. Гидростатическое давление в любой данной точке жидкости одинаково по всем направлениям, т.е. не зависит от угла наклона площадки действия.

Единица измерения давления – 1Па = 1 Н/м²

1 атм = 1 = 98100Па = 0,1МПа.

3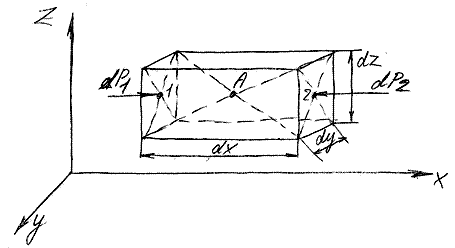 .Дифференциальные уравнения равновесия жидкости (уравнения Эйлера)

Это уравнение относится к идеальной жидкости.

dx, dy, dz – размеры объема по координатным осям.

А – середина.

Дано жидкое тело, массой М, плотностью , которое находится в равновесии под действием внешних сил. Равнодействующую этих сил обозначим F.

Выберем декартову систему координат в которой находится тело. Сила F может быть разложена на 3 составляющие:

F= f(F_x ;F_y; F_z)

Г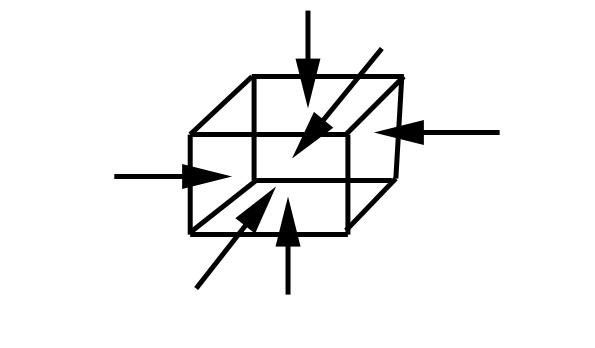 де - это в соответствии со 2-м законом Ньютона – проекции ускорений, вызываемых внешними силами на соответствующие координатные оси.

Выделим в жидком теле бесконечно малый объем с центром в точке А в форме прямоугольного параллелепипеда, грани которого параллельны координатным осям. Мысленно отбрасываем окружающую параллелепипед жидкую среду. Заменяем жидкую среду эквивалентными силами.

Поскольку жидкое тело находится в равновесии, соответственно и выделенный объем, то

- условие равновесия вдоль оси х.

- проекция на ось х элементарной массовой силы.

Элементарная масса прямоугольного параллелепипеда :

- элементарный объём нашего параллелепипеда

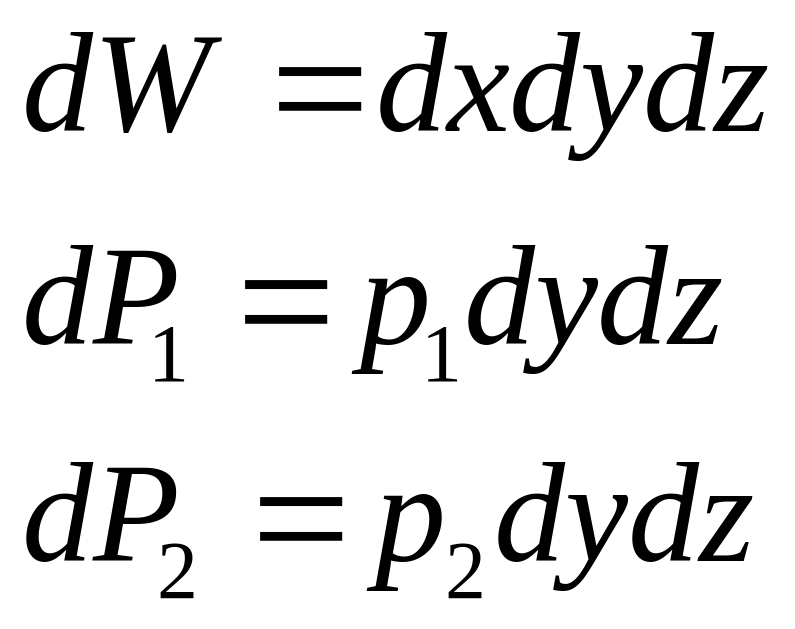
и - давление в точках 1 и 2.

А – центр тяжести рассматриваемого элементарного объёма .

Давление в точке А=р.

Направление оси х может быть представлено частной производной :

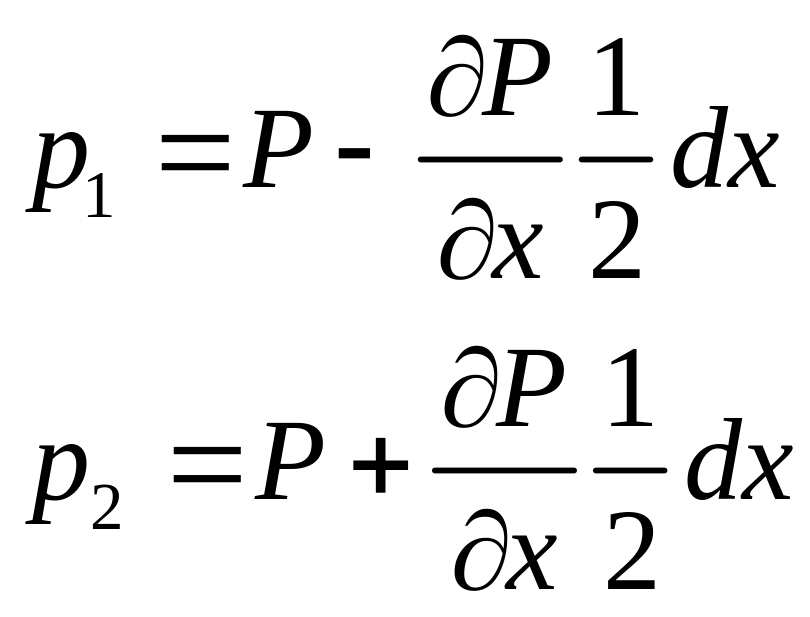
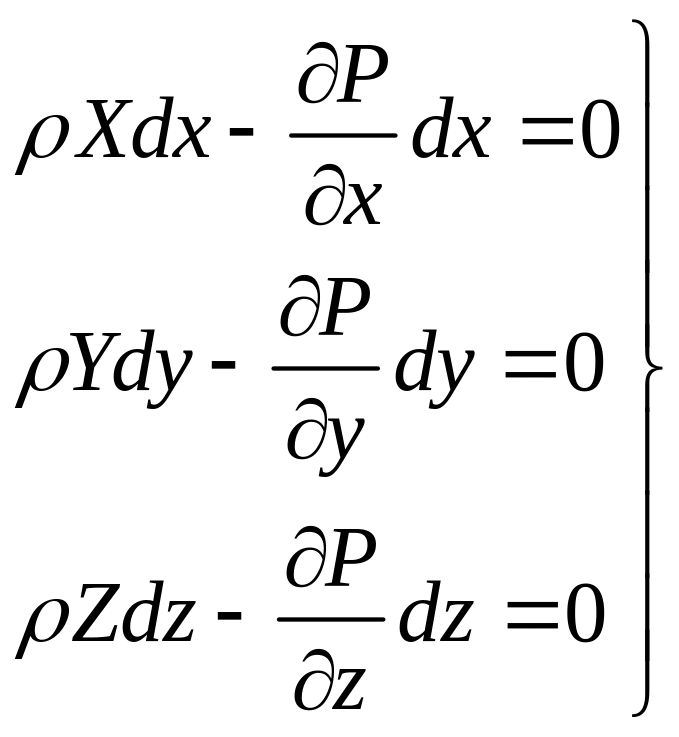
Обе части полученной системы можно разделить на константу и получим:

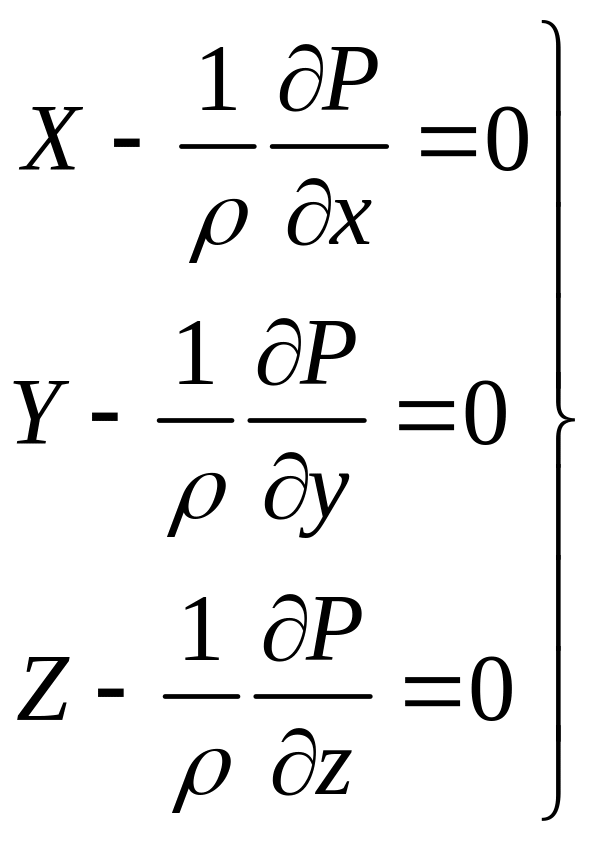
Сложим все 3 уравнения и получим следующую формулу:

- основное уравнение гидростатики.