5.4 Проверка устойчивости верхней части колонны

Проверку устойчивости верхней части колонны в плоскости действия момента выполняем по формуле:

, (5.17)

Определяем гибкость:

тогда

, (5.18)

.

Значение коэффициента  принимаем по / 2 /

тогда и

- условие выполняется.

Недонапряжение -

Проверяем устойчивость верхней части колонны из плоскости действия момента по формуле

, (5.19)

где _y – коэффициент продольного изгиба, определяемый в зависимости от гибкости

; y = 0,9076.

Для определения m_x находим максимальный момент в средней трети расчетной длины верхней части колонны по формуле

, (5.20)

Относительный эксцентриситет:

m_x=M^I_X ∙ A/(N ∙W_X)=540,06∙100∙169/(491∙2884,95)=6,443.

Значит с определяем по формуле

, (5.21)

где при m_x=5,

при m_x=10.

где ,  и _b - коэффициенты, определяемые по / 2 /

коэффициент  = 1,0; так как

_b=1 в большинстве случаев при проверке устойчивости колонн,

тогда ,

,

Определим предельную гибкость и сравним ее с расчетной:

λ_u=180-60∙α , (5.22)

α=σ/Ry∙γc=202,47/240∙1=0,844

λu=180-60∙0,844=129,43> λy=36,32

Так как ослабления в сечении колонны отсутствуют и m_x< 20 проверку прочности с учетом развития пластических деформаций не выполняем.

Проверяем местную устойчивость стенки при изгибе колонны из плоскости действия момента.

Наибольшие сжимающие напряжения на краях стенки определим по формуле:

, (5.23)

на одном краю

;

на противоположном краю

.

Средние касательные напряжения в стенке определяются по формуле:

, (5.24)

где Q – поперечная сила в сечении 1-1, определенная при расчете поперечной рамы.

Определим коэффициент α с учетом знаков σ и σ₁:

, (5.25)

,

При α=1,74 > 1 наибольшее отношение h_ef/t_w определяем по формулам:

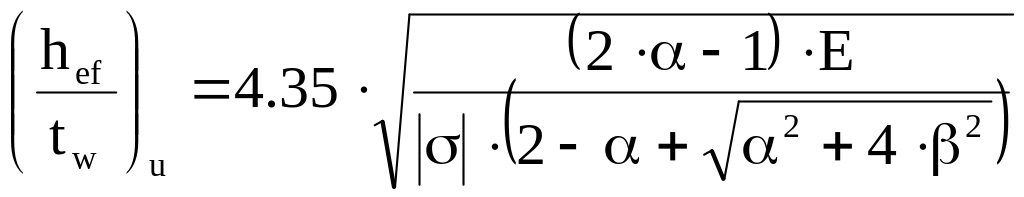, (5.26)

=3,8 , (5.27)

где β=1,4(2α-1) /σ =1,4(21,74-1)23,17/222,95=0,361

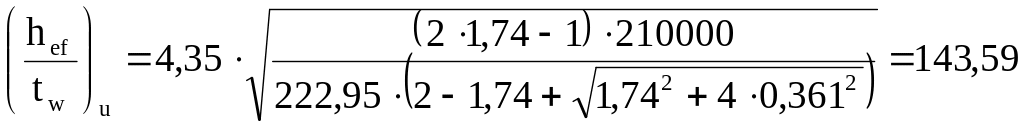
=3,8

Так как определенное по формуле (5.26) больше чем отношение, определенное по формуле (5.27), то принимаем =112,4.

Так как = < =112,4, то местная устойчивость стенки обеспечена.

При =41<2,3 =2,3 , стенку не следует укреплять поперечными ребрами жесткости

5.5 Подбор сечения нижней части колонны

Сечение нижней части колонны сквозное, состоящее из двух ветвей, соединенных решеткой. Высота сечения h_н = 1000мм. Подкрановую ветвь колонны принимаем из широкополочного двутавра, наружную –из швеллера.

Определим ориентировочное положение центра тяжести сечения по формулам / 2 /, принимая z₀ = 3см; тогда h₀ = h_н - z₀ =100 - 3 =97см.

, (5.28)

.

y₂ = h₀ - y₁ , (5.23)

y₂= 97 – 55,29 = 41,714см

Определяем продольные усилия в подкрановой и наружной ветвях N_в1, N_в2, кН, по формулам / 2 /

(5.24)

Находим требуемые площади ветвей по формулам /2/, при этом задаемся =0,8

(5.25)

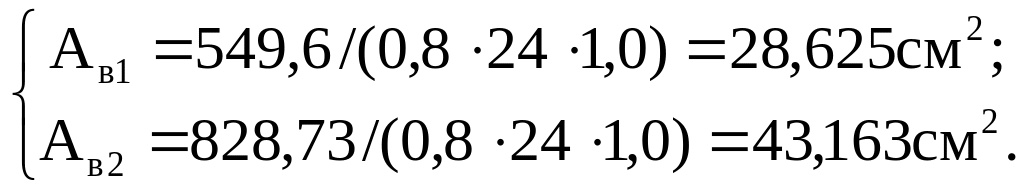
Для подкрановой ветви по сортаменту подбираем двутавр №36 со следующими параметрами:. А=61,9см²; i_x1 =14,7см, i_y =2,89см, I_x1=13380 см⁴, I_у =516 см⁴ .

Сечение наружной ветви принимаем из швеллера №36 со следующими параметрами: A=53,4см², I_x2=10820 см⁴, I_у =513 см⁴, i_x2 = 14,2см, i_y = 3,1см; z_O =2,68 см.

Уточняем положение центра тяжести сечения нижней части колонны:

h₀ = h_н - z₀ = 100 – 2,68 = 97,32cм

Уточняем усилия в ветвях с учетом фактических у₁, у₂: