3.5 Проверка прочности сечения подкрановой балки
Расчет на прочность подкрановых балок выполняем согласно требований /1/.
Проверку прочности стенки балки от действия местных напряжений под колесом крана производим по формуле /1/
,
(3.29)
где γf1 - коэффициент увеличения вертикальной сосредоточенной нагрузки на отдельное колесо крана, принимаемый согласно /3/ в зависимости от группы режимов работы кранов; принимаем γf1 = 1,1;
lef - условная длина распределения усилия Fki; определяемая по формуле /1/
,
(3.30)
здесь с - коэффициент, принимаемый для сварных и прокатных балок 3.25, для балок на высокопрочных болтах 4.5; принимаем с = 3.25;
I1f - сумма собственных моментов инерции пояса балки и кранового рельса или общий момент инерции рельса и пояса в случае приварки рельса швами, обеспечивающими работу рельса и пояса /2/,
,
(3.31)
где Iр - момент инерции кранового рельса; принимаем Ip = 1547,4 см4;
см4;
см;
Па
=25,45 МПа
240 МПа.
Условие выполняется.
Проверку нормальных напряжений в верхнем поясе подкрановой балки (в нашем случае точка А - рисунок 3.3) осуществляем по формуле /2/
,
(3.32)
где
- момент сопротивления сечения относительно
оси х-х, определяем по формуле /2/,
,
(3.33)
-
момент сопротивления сечения относительно
оси у-у, определяем по формуле /2/,
,
(3.34)
Ix- момент инерции сечения относительно оси х-х;
,
(3.35)
cм4;
см3;
Iy- момент инерции сечения относительно оси y-y;
,
(3.36)
см4;
,
(3.37)
см;
см3;
МПа
240 МПа.
Условие выполняется.
В сжатой зоне стенок подкрановых балок из стали с пределом текучести до 400 МПа должны быть выполнены условия /1/
,
(3.38)
;
, (3.39)
,
(3.40)
здесь
;
коэффициент,
принимаемый равным 1.15 для расчета
разрезных балок и 1.3 для расчета сечений
неразрезных балок; принимаем
МПа;
МПа;
МПа;
МПа;
МПа
МПа;
Мt - местный крутящий момент, определяемый по формуле /1/
(3.40)
e - условный эксцентриситет, принимаемый равным 1.5 см;
кНм;
hp=120мм - высота кранового рельса;
МПа;
МПа.
Проверяем условия (3.39)
225,78+6,36=232,14 МПа 240 МПа,
25,45+5,59=31,04 МПа 240 МПа,
17,2+7,64+1,398=26,238 МПа 138,6 МПа.
Условия выполняются.
Проверим балку на устойчивость.
Расчет на устойчивость балок двутаврового сечения, изгибаемых в плоскости стенки следует выполнять по формуле /1/
,
(3.41)
где τcr – критические напряжения;
cr
,
(3.42)
где λef – условная приведенная гибкость,
μ – отношение большей стороны пластины к меньшей (в зависимости от размеров – высоты стенки балки и расстояния между двумя соседними ребрами жесткости – а, которое принимаем равным–1,5 м);
,
(3.43)
Так как hct<a, то
=а/hct, (3.44)
и значения σсr и σloc,cr будем определять исходя из следующих условий а/hct=150/65=2,31>0.8, но так как отношение σloc,x/σx=6,36/225,78=0,028 меньше значений, указанных в/1/, по следующим формулам:
,
(3.45)
где сcr–коэффициент, принимаемый для сварных балок в зависимости от коэффициента δ*;
,
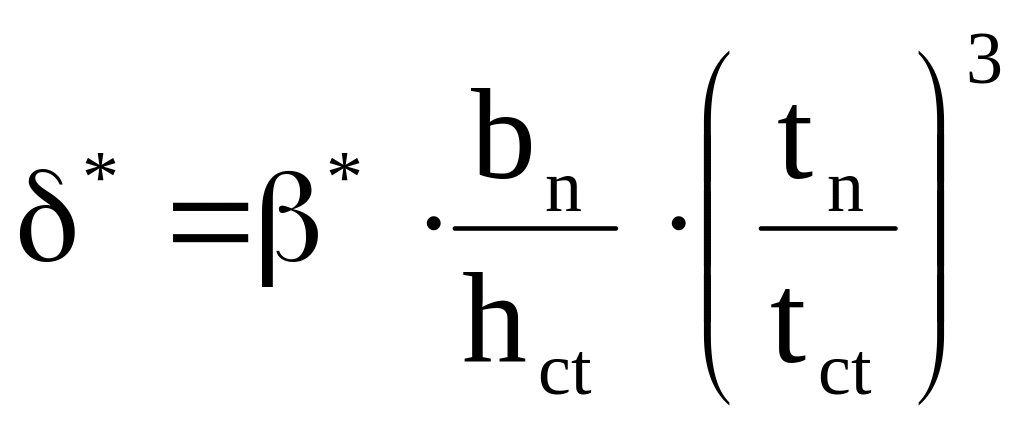(3.46)
где β* – коэффициент принимаемый для подкрановых балок, если крановые рельсы не приварены к балкам – 2.
,
(3.47)
где с1 – коэффициент принимаемый в зависимости от отношения а/hct и значения δ*,
,
(3.48).
Нормальные напряжения(в уровне верхней кромки стенки):
σ=М·yc/Ix, (3.49)
где М – значение изгибающего момента в расчетном сечении;
yc=0,5·hct=0,5·65=32,5см,
σ=141363,2∙325/246120,83=18,966кН/см2=189,66 МПа
Касательные напряжения в середине пролета можно определить по формуле:
τ=Q/(tct·hct), (3.50)
где Q – наибольшая поперечная сила при расположении колес крана как для определения момента М. В нашем случае она равна 148,26кН
Рисунок 3.4 – Для определения Q в сердине пролета, при расположении колес крана как для определения момента М.
τ=148,26/(0,8·65)= 2,85 кН/см2=28,51 МПа
По δ* определяем сcr=35,5 и с1=83,6
На основании полученных выше значений определяем σсr и σloc,cr:
Мпа,
МПа,
τcr
МПа,
.
Условие выполняется, следовательно устойчивость балки обеспечена.